数学思想方法在二次函数中的应用
2019-11-04庄梅芳
庄梅芳
(福建省晋江市南湾中学 福建 晋江 362200)
1.分类讨论思想在二次函数中的应用
分类讨论思想是一种重要的数学思想,在解决二次函数问题时经常用到。许多二次函数问题,往往在相同的题设下,会产生几种不同的结果,这就需要借助于分类讨论思想按照同一标准,确定分类对象,把可能存在的一切情况都列举出来,一一加以研究,然后进行归纳,合并,综合得出结论。
例1,已知抛物线y=ax2+bx+c(a>0),它与x轴交于点A和B,与y轴交于点C,试求S△AoC+S△BoC
解:设A(x1,0),B(x2,0)则x1,x2就是二次方程ax2+bx+c=0的两个实根。
而OA=|x1|,OB=|x2|, 又由x=0时,y=c得OC=|c|
已知a>0,下面就c的不同符号分别计算S△AoC+S△BOC的值
(1)当c=0时,显然有S△AoC+S△B0C=0
(2)当c>0时,x1和x2同号
i)若x1和x2都为正数,则b<0,
ii)若x1和x2都为负数,则b>0
(3)当c<0时,x1和x2异号,不防设x1>0,x2<0,则
OC=|c|=-c
2.转化思想在二次函数中的应用
转化思想是一种最基本的数学思想,是解决二次函数问题不可忽视的方法。二次函数的问题一般都是综合性很强的题目,如何把复杂的问题向简单的问题转化,是解题成败的关键所在。转化思想在二次函数中运用的思想一般是把生活、生产、科研中的实际问题通过建立数学模型转化为数学问题;把几何问题转化为函数问题;把位置关系转化为数量关系;把非常规问题转化为常规问题,最终实现未知向已知的转化,从而使问题得到解决。
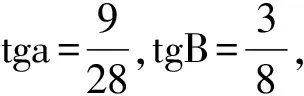
(1)若导弹运行轨道为一抛物线,求该抛物线的解析式;
(2)说明按(1)中轨道运行的导弹能否击中目标C的理由。
解:(1)设导弹运行轨道的抛物线解析式为y=ax2+bx+c,由题意知,这条抛物线的顶点坐标为E(4,3)
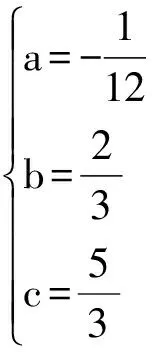
(2)设C点的坐标为(xo,yo),过C作CB⊥0X垂足为B,在Rt△OBC和Rt△ABC中,OA=1,
3.方程思想在二次函数中的应用
方程思想是一种广泛应用的数学思想,是解决二次函数问题的一个有力工具。在二次函数问题中,或多或少存在着等量关系,我们经常把所研究的二次函数问题中的数量关系,转化为方程或方程组等数学模型,通过解方程或方程组,实观未知向已知的转化。可见,方程思想方法,对解决二次函数问题,作用十分重大。如待定系数法求二次函数解析式,求解几何图形中的函数关系,求二次函数与其他图形的交点问题等,都离不开方程思想。
例3已知二次函数y=x2+bx+a(b<0)的图像与y轴交于点P(0,3),与x轴交于A、B两点,且AB=2
(1)求bc的值,并写出这个函数的解析式;
(2)过P点作x轴的平行线,求这条平行线被二次函数图像所截得的线段的长;
(3)求△PAB的面积;
解:(1)∵P(0,3)在图像上,将其坐标值代入y=x2+ bx+c(b 即得c=3设A(x1,0),B(x2,0),则x1、x2是方程x2+bx+3=0的根。 ∵AB=2,即|x1-x2| ∵b<0, ∴ b=-4 ∴所求的解析式为y=x2-4x+3 (2)设过P且平行于x轴的直线与图像的另一交点为Q,则P、Q的坐标就是下面方程组的解: 数形结合思想是一种典型的数学思想,是研究二次函数问题离不开的思想方法。数学是以现实世界中的空间形式与数量关系为研究对象,即数学是研究数、形及其关系的一门科学。在建立直角坐标系后,平面上的点就可以用坐标来表示,进一步又可建立平面上曲线与方程间的联系,这就使数与形结合起来,二次函数问题正是这种思想的充分体现,使数和形的结合达到了一个新的境地。在二次函数问题中,我们通过图形形象直观地表示出抽象的数量关系,即利用形来研究数,另一方面,通过数量计算准确地表示出图形的性质即利用数来研究形。数形结合思想的运用,是验证二次函数解题能力和创造性的有力根据。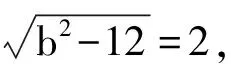

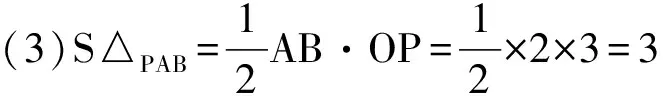
4.数形结合思想在二次函数中的应用
