基于被动水声信号的淡水鱼混合比例识别
2019-11-04黄汉英杨咏文赵思明熊善柏涂群资
黄汉英 杨咏文 李 路 赵思明 熊善柏 涂群资
(1.华中农业大学工学院, 武汉 430070; 2.华中农业大学食品科技学院, 武汉 430070)
0 引言
我国是淡水鱼养殖大国,在鱼类养殖过程中,采用多品种合理混养与密养是实现高产的有效措施,因此鱼类混合比例和数量识别在渔业资源调查和养殖监测中具有重要意义。被动水声技术是鱼类监测中常用的方法,其研究主要集中在海洋鱼类的发声特点[1-4]、鱼类资源调查[5-9]、行为特征[10-13]等方面。然而,淡水鱼和海水鱼的发声机理及生活习性不同,鱼声信号也不相同,目前针对淡水鱼的研究较少。文献[14]主要研究了淡水鱼水声信号特征参数的提取方法,使用概率神经网络分类器建立了淡水鱼品种识别模型;文献[15]利用多元线性回归算法建立了淡水鱼数量估计模型;文献[16]分析了鱼的种类和数量与频段能量、平均Mel频率倒谱系数等特征之间的关系。这些研究仅仅涉及到单品种淡水鱼的种类和数量,针对淡水鱼混合比例和数量识别的研究鲜见报道。
针对上述问题,本文研究不同混合比例的淡水鱼水声信号,提取其特征参数,运用基于主成分分析(Principal component analysis,PCA)的支持向量机(Support vector machine, SVM)模型进行淡水鱼混合比例识别。
1 材料与方法
1.1 材料和仪器
选取鳊鱼、鲫鱼作为试验材料,在华中农业大学市场购买鳊鱼、鲫鱼各4尾。其中鳊鱼每尾0.4~0.7 kg,鲫鱼每尾0.3~0.6 kg。
淡水鱼被动水声信号采集装置如图1所示,其主要包括SM2+型声学记录仪、HTI-96-MIN型水听器和隔音鱼箱。鱼箱高为73 cm,直径为60 cm,壁厚为0.5 cm,容积约为200 L。鱼箱外表面覆盖隔音海绵,以减弱外界噪声对试验的干扰,其中试验鱼箱采集鱼声信号,对照鱼箱采集环境背景噪声,用于后续信号预处理。
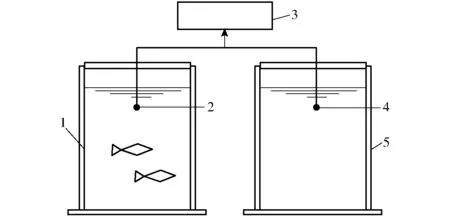
图1 淡水鱼被动水声信号采集装置示意图Fig.1 Sketch of freshwater fish passive acoustic signal acquisition device1.试验鱼箱 2.1号水听器 3.声学记录仪 4.2号水听器 5.隔音海绵
1.2 方法
1.2.1信号采集
利用淡水鱼被动水声信号采集装置采集混养鳊鱼和鲫鱼的声音信号。首先往水箱中注入约160 L水,将水听器置于水面以下25 cm处,测量试验环境参数,其中水温为15~20℃,pH值为7.5~8.0,溶氧量为7~8 mg/L。将鳊鱼和鲫鱼分别按4∶1、3∶1、2∶1、1∶1、1∶2、1∶3、1∶4(分别用1~7作为分类标签)的比例放入水箱中,其中每种比例中的“1”代表鱼的数量为1尾,静置10 min后开始信号采集。设置声学记录仪的采集时长为1 min,采样频率为4 000 Hz,每种混合比例各采集120个样本,共采集840个鳊鱼和鲫鱼混合比例的水声信号样本。
1.2.2信号预处理
采集的淡水鱼水声信号样本中含有噪声,因此在提取水声信号特征之前需要进行滤波、消噪等预处理。运用Cool Edit Pro数字音频编辑器消除鱼声信号背景环境噪声,并在Matlab 2014a软件下采用butter函数进行滤波,其中滤波器的阶数为4,截止频率为1 000 Hz。
1.2.3样本集划分
将采集的840个鳊鱼和鲫鱼混合比例的水声信号样本进行信号预处理后,运用SPXY(Sample set partitioning based on joint X-Y distance)法[17]划分样本。为了使训练的样本数据覆盖更均匀和广泛,以保证每一种比例的识别率,首先将数据按照比例分组,然后在每组内分别使用SPXY法按4∶1的比例将数据划分为训练集和测试集,即训练样本共672个,测试样本共168个。
1.2.4特征参数提取
鱼声信号与语音信号在声学特征方面具有相似性,而在很多语音信号处理中,都会涉及到短时平均能量、短时平均过零率等,因此利用文献[18]中的计算公式提取了短时平均能量和短时平均过零率,并通过功率谱分析提取了主峰频率和主峰值。
Mel频率是基于人耳听觉特性提出来的,Mel频率倒谱系数是利用其与频率的非线性对应关系计算得到的频谱特征,在语音识别领域应用广泛。本文将预加重后的鱼声信号进行分帧处理,并选用Hamming窗作为窗函数,通过三角Mel带通滤波器进行滤波,提取了12维平均Mel频率倒谱系数。
由于鱼声信号具有明显的时变特性,单独的时域特征或者频域特征都无法客观地反映鱼声信号的全部特征。而小波包分解是一种可以获取信号时频局部特征的方法,适用于鱼声信号的提取。因此本文采用4层小波包分解,选取正交小波作为小波包基函数,再结合重构算法得到各频段重构信号的能量,提取了16维频段能量特征。
将上述所提取的特征采用Z-score[19]进行标准化,建立鱼声信号特征向量X=(x1,x2,…,x32),其中x1为短时平均能量,x2为短时平均过零率,x3~x18为小波包分解频段能量,x19~x30为平均Mel频率倒谱系数,x31为功率谱主峰频率,x32为功率谱主峰值。
1.2.5主成分分析原理
所提取的水声信号特征间可能存在较强的相关性,而主成分分析[20]运用降维的思想能将原本具有一定相关性的指标经过正交变换重组为互不相关的综合指标,因此进行主成分分析可以进一步降低噪声对分类结果的影响,提高识别正确率。主成分分析的数学模型为
(1)
式中ujp——标准化系数
xip——第i个水声信号样本的第p个标准化特征
zij——第i个水声信号样本的第j个主成分变量
经过主成分分析后鱼声信号特征向量为Zi=(zi1,zi2,…,zij),用于淡水鱼混合比例识别。
1.2.6分类器设计
基于被动水声信号的淡水鱼混合比例识别本质是对淡水鱼水声信号进行分类。本文采用基于PCA的支持向量机分类算法实现淡水鱼的混合比例识别,并与支持向量机、概率神经网络、Fisher线性分类器模型的识别效果进行比较。
支持向量机是一种基于结构风险最小原则的模式识别方法[21]。其主要思想是将样本空间的数据映射到高维空间,并在高维空间中寻找一个超平面,使得超平面与不同样本集间的距离最大,以保证最小的分类错误率。本文构造软边距最优超平面,引入非负松弛变量ξi,为使训练样本(Zi,Yi)尽可能被正确分类,则需满足
Yi(ωZi+b)≥1-ξi
(2)
式中ω——超平面的法向量
b——超平面截距
Yi——第i个水声信号样本对应的分类标签
在约束条件式(2)下,分类超平面的最优问题为
(3)
式中C——惩罚系数N——训练样本数
其对偶问题为
(4)
式中α——Lagrange系数
K(Zi,Zm)——核函数
αi——第i个样本对应的Lagrange系数
αm——第m个样本对应的Lagrange系数
Ym——第m个水声信号样本对应的分类标签,m≠i
相应的分类决策函数为
(5)
式中Z——待分类样本 sgn(·)——符号函数
ft(Z)——第t类标签对应的决策函数
将Z代入决策函数ft(Z),若ft(Z)>0,且fq(Z)<0(t、q=1,2,…,7,t≠q),则将其归为第t类,反之归为第q类。
选用径向基函数(Radial basis function,RBF)作为支持向量机的核函数,其公式为
K(Zi,Z)=exp(-γ‖Z-Zi‖2)
(6)
惩罚系数C、核函数参数γ的选取会影响支持向量机算法的识别效果。而粒子群优化算法(Particle swarm optimization,PSO)[22]是一种群体智能优化算法,可以在较大范围内快速地寻找C和γ最优值,提高搜索效率和识别正确率。
1.2.7模型评价标准
选用Kappa系数[23]和平均识别正确率来评价分类器模型的性能。Kappa系数是一种衡量多分类问题分类精度的指标,能够计算样本数据的整体一致性和分类一致性。Kappa系数在实际应用中通常取[0,1],越大表示模型分类精度越高。计算公式为
(7)
其中
(8)
(9)
式中Po——平均识别正确率
at——第t类样本被识别正确的个数
n——总样本个数
bt——第t类样本的个数
ct——预测结果中第t类样本的个数
Po直观反映了分类器的性能,平均识别正确率越高,分类器越好。
2 结果与分析
2.1 鱼声信号
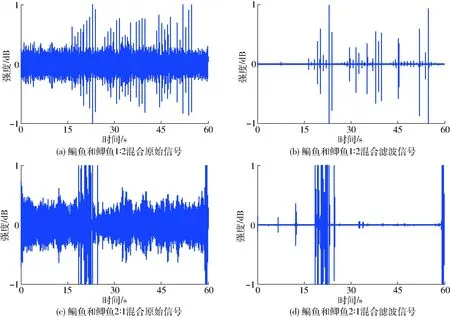
图2 不同样本水声信号消噪前后时域波形Fig.2 Diagrams of time domain waveform before and after denoising of different samples
图2分别为2种不同混合比例的鳊鱼、鲫鱼水声信号样本滤波前后的时域波形。由图2可知,采取butter函数的滤波方法可以有效地减弱噪声干扰,鳊鱼和鲫鱼1∶2与2∶1混合比例的水声信号时域波形存在差异。
每种比例120个样本的特征参数平均值计算公式为
(10)
为突出每一种比例的水声信号特征,将每种比例的32个特征参数平均值绘制成折线,结果如图3所示。由图3可知,不同混合比例的水声信号样本特征参数平均值存在一定的差异,虽然短时平均能量(p=1)、短时平均过零率(p=2)以及主峰频率(p=31)和主峰值(p=32)的曲线存在近似重合的情况,无法将不同混合比例的水声信号完全区分,但不同混合比例的水声信号样本的小波包分解频段能量(p=3,4,…,18)和平均Mel频率倒谱系数(p=19,20,…,30)的曲线波动较明显。
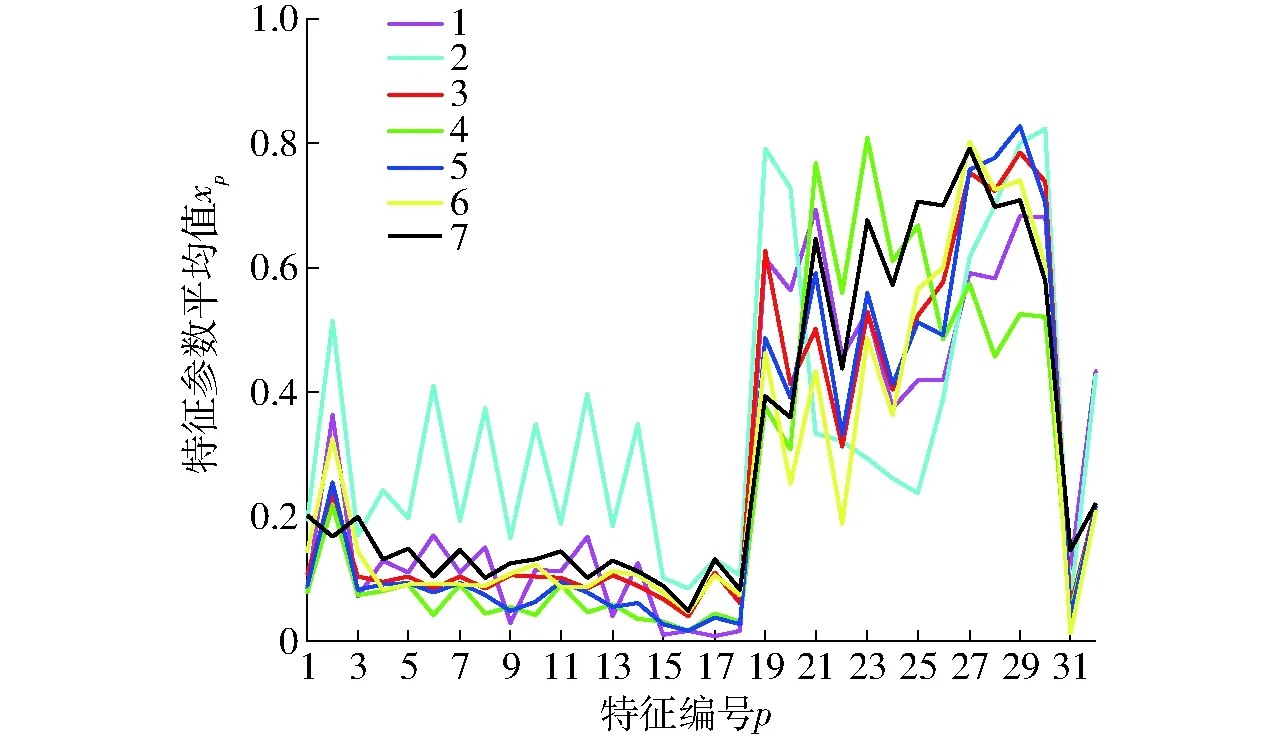
图3 7种混合比例水声信号样本特征参数平均值Fig.3 Average value of characteristics of seven classes acoustic signal samples
2.2 鱼声信号特征参数显著性分析
7种混合比例的水声信号样本特征参数显著性分析结果如表1所示。由表1可知,在提取的32个水声信号特征中,只有平均Mel频率倒谱系数(p=19,20,…,30,且p≠26)能将第4类和第5类混合比例的水声信号显著区分,不同混合比例水声信号样本的特征之间存在一定差异,主峰值(p=32)的差异最小,平均Mel频率倒谱系数的差异最大。由此可知,本文提取的32个特征可以用于淡水鱼混合比例识别,且平均Mel频率倒谱系数对于淡水鱼混合比例识别效果最优。
2.3 基于PCA的支持向量机分类模型
2.3.1主成分分析
对提取的32个特征进行主成分分析,其贡献率分布如图4所示。由图4可知,主成分贡献率急剧下降,特征值大于1的前4个主成分贡献率分别为43.57%、26.17%、11.81%、6.04%,累计贡献率达到87.59%,代表了原始数据的大部分信息,说明所提取的32个特征之间具有较强的相关性,在实际应用中,可根据识别精度的要求通过主成分分析适当地对特征进行压缩,从而提高识别效率。
2.3.2主成分个数对模型识别率的影响
以主成分分析得到的特征Zi建立支持向量机模型,得到7种混合比例的平均识别正确率与主成分个数的关系如图5所示。由图5可知,前4个主成分的测试集平均识别正确率为84.52%,前19个主成分的测试集平均识别正确率达到96.43%,随着选用主成分个数的增加,模型的平均识别正确率急剧提高,当主成分个数少于10时,受测试样本数和样本集划分的影响,存在训练集平均识别正确率低于测试集平均识别正确率的情况,当主成分个数达到19时,训练集和测试集的平均识别正确率均达到最大值且保持不变。因此,本文选用前19个主成分作为特征进行淡水鱼混合比例识别。

表1 7种混合比例的水声信号样本特征参数显著性分析Tab.1 Characteristic significance analysis of acoustic signal samples of seven classes
注:A、B、C表示组间数据在0.01水平上差异显著,字母不同表示差异极显著。
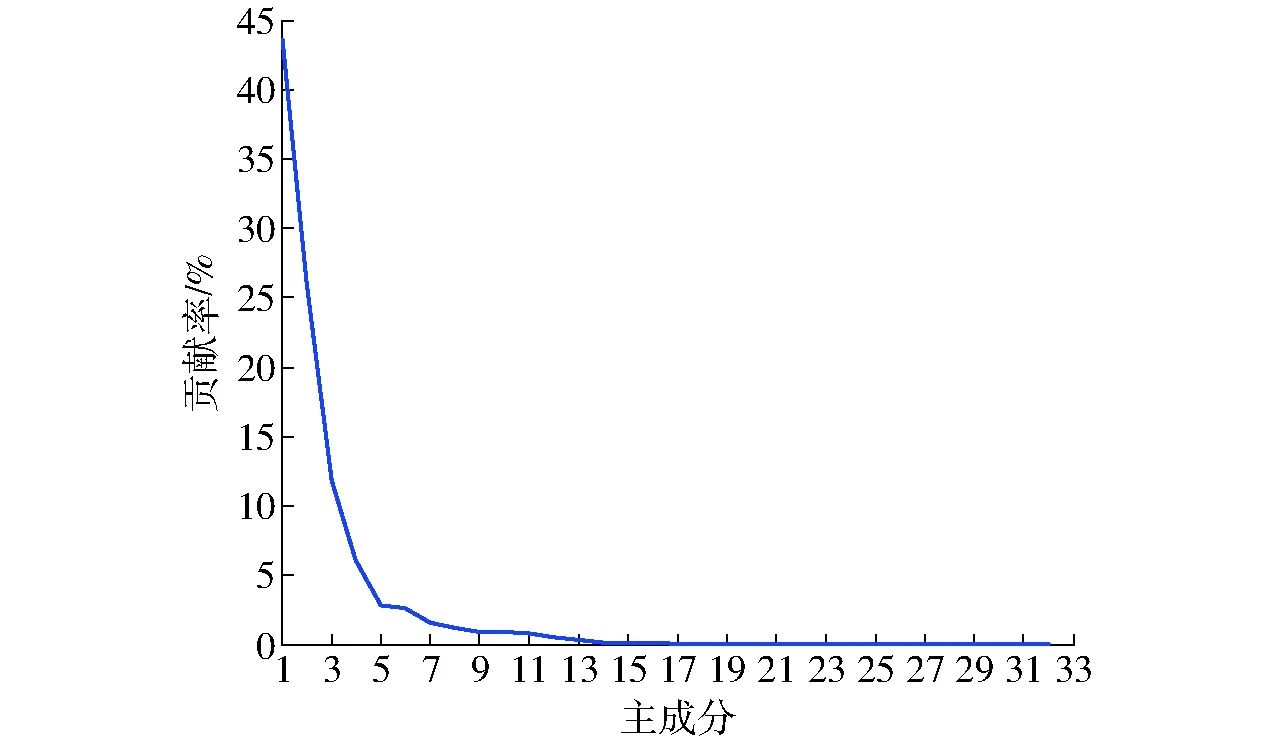
图4 主成分贡献率分布Fig.4 Distribution of principal component contribution rate

图5 主成分个数与平均识别正确率的关系Fig.5 Relationship between number of principal components and average recognition rate
2.3.3模型评价
不同模型识别效果比较如表2所示。由表2可知,Fisher线性分类器模型的训练集和测试集平均识别正确率均最低,Kappa系数最小,概率神经网络模型的训练集平均识别正确率较高,但测试集平均识别正确率低于PCA-SVM模型,模型泛化能力较差,PCA-SVM模型的训练集和测试集平均识别率均高于SVM模型,测试集Kappa系数最大,因此模型泛化能力较强,分类精度较高。结果表明,PCA可以提高模型的识别率,PCA-SVM模型具有良好的分类识别能力,适用于淡水鱼混合比例识别。
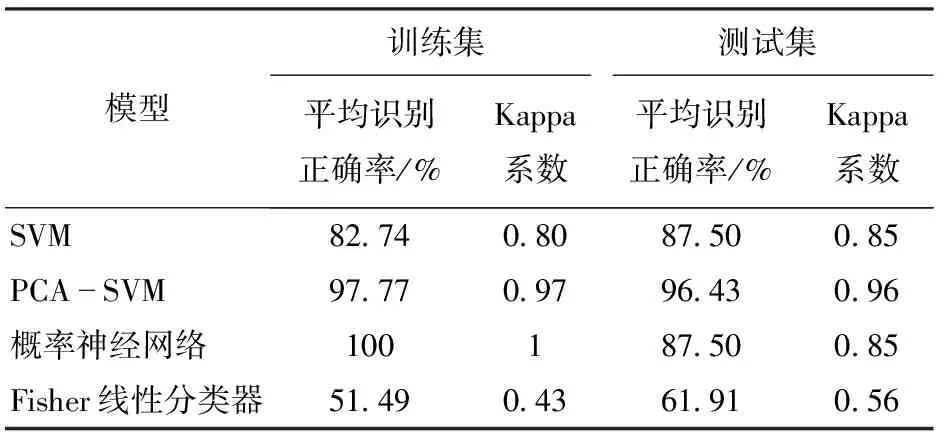
表2 不同模型识别效果比较Tab.2 Recognition effects comparison of different models
3 结束语
研究了7种混合比例的鳊鱼和鲫鱼被动水声信号,分别提取了短时平均能量、短时平均过零率、4层小波包分解频段能量、12维平均Mel频率倒谱系数、基于功率谱的主峰频率和主峰值等共32个特征,分析了不同混合比例水声信号特征的显著性差异,建立基于PCA的支持向量机分类模型,探讨了主成分个数与平均识别正确率的关系,比较了不同模型的识别效果。结果表明,平均Mel频率倒谱系数对于淡水鱼混合比例识别效果最优,基于PCA的支持向量机模型的平均识别正确率较高,选用19个主成分进行比例识别时平均识别正确率达96.43%,Kappa系数为0.96,适用于淡水鱼混合比例识别。
