基于混合聚类分析的共享单车停放点位置合理性研究

王霞 宋树华 汤军 刘远刚

摘要：针对共享单车停放点位置优化的问题，以现有的共享单车停放点位置作为初始聚类中心点，对共享单车的定位数据做聚类，并且提出了结合K-MEANS聚类和缓冲区分析的混合聚类方法，来解决初始聚类中心点相靠近时出现的共享单车错误分类问题。将最终聚类结果作为建议的共享单车停放点位置，进而依据建议的共享单车停放点位置判断现有的共享单车停放点位置的合理性，实验结果表明这种混合聚类方法的聚类效果理想。

关键词：混合聚类;共享单车;停放位置;合理性

中图分类号：TP301.6 文献标识码：A 文章编号：1007-9416（2019）07-0058-04

共享单车作为中国“新四大发明”之一，弥补了市民出行过程中“最后一公里”的空白。它为市民个人的出行需求提供了极大便利，但是共享单车的过度投放和疏于管理也阻碍着城市文明的建设[1]。

共享单车停放点位置的确定是展开共享单车规范化管理工作的第一步，在停放点选址问题上[2-5]，很多学者都选择采用划分法[6，8]或者层次法[7，8]对共享单车位置分布数据进行聚类。这些聚类方法得出的聚类结果未考虑已规划停放点的位置合理性，而且当已规划停放点的中心位置相邻时，聚类的结果并不理想。

本文提出了结合K-MEANS聚类[9]与缓冲区分析的混合聚类方法，基于模拟数据采用混合聚类方法对停放点的位置合理性进行判断，以求得到在已规划的停放点中心位置相邻情况下理想的聚类结果。

1 共享单车停放点位置合理性分析

1.1 共享单车停放点位置合理性问题分析

评价一个停放点的位置是合理的，即要避免出现以下情况：（1）已经施划的停放点内没有或长期只有很少数量的单车停放;（2）在经常有一定数量单车停放的地点没有施划停放点。现有停放点的选址主要依靠政府的土地规划政策和规划人员的经验，存在一定施划上的合理性但是对停放需求点的预测还不够准确。

普遍认为，单车的停放位置在空间上数量多且集聚，则空间上形成的集聚区域可视为有单车停放需求的地点。由此可见，停放点的施划与共享单车停放位置的分布情况有很大的关联性，因此可以借助共享单车的定位数据结合现有停放点位置数据做聚类分析，得出的聚类结果的中心位置为有单车停放需求的地点，以有单车停放需求的地点为依据再对现有停放点的位置做出调整，能够提高共享单车停放需求点预测的准确度。

1.2 基于混合聚类的共享单车停放点位置合理性判断

本文提出的混合聚类结合了K-MEANS聚类和缓冲区分析[10]，本文称引入缓冲区分析的聚类为缓冲区聚类。缓冲区聚类是为了解决现有停放点位置靠近时，可能会出现单车定位数据错误分类的情况。缓冲区聚类在以下应用场景中有现实意义，比如现有停放点施划在较狭窄马路的两边或是密集施划在商业繁华地段时，若只对单车定位数据进行简单的聚类，那么可能会出现聚类结果不准确的结果。

下面从缓冲区距离和缓冲区聚类算法描述两方面说明缓冲区聚类。

1.2.1 缓冲区距离确定的算法描述

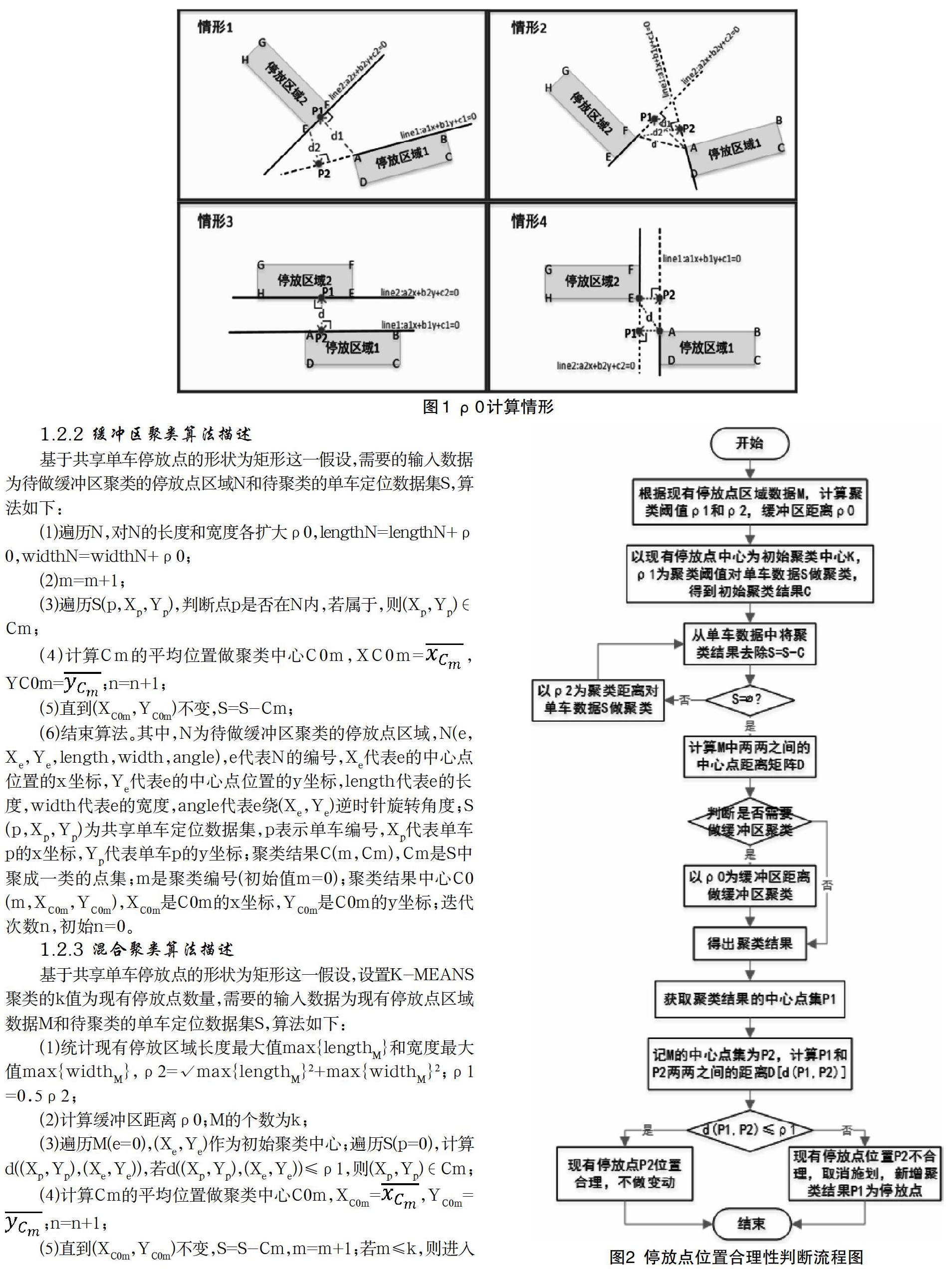
在进行缓冲区聚类之前首先要确定缓冲区距离，确定缓冲区距离的情形见图1，基于共享单车停放点的形状为矩形這一条件假设，需要输入的数据为现有停放点区域数据M，确定缓冲区距离的算法如下：

（1）计算M两两之间中心点距离D，取min{D}的两个现有停放区域记为停放区域1（R1）和停放区域2（R2）;

（2）确定line1和line2的直线方程;

（3）计算d1和d2;

（4）确定ρ0，ρ0=0.5d;判断P（P1、P2）是否在R（R2、R1）上，若P落在R上，则对应的距离为有效距离，反之则为无效距离;取d1和d2中标记为有效距离的计算ρ0，若d1和d2都标记为无效距离，则计算R1所有顶点和R2所有顶点的最短距离标记为有效距离计算ρ0。（注：情形3和情形4为直线斜率为0和无穷的特殊情况，ρ0的计算步骤一样。）;

（5）结束算法。其中，M为现有停放点区域数据，M（e，Xe，Ye，length，width，angle），e代表M的编号，Xe代表e的中心点位置的x坐标，Ye代表e的中心点位置的y坐标，length代表e的长度，width代表e的宽度，angle代表e绕（Xe，Ye）逆时针旋转角度; line1为经过R1两个顶点的直线，且R1和R2上的所有顶点分别分布在line1的左右两侧;line2为经过R2两个顶点的直线，且R1和R2上的所有顶点分别分布在line2的左右两侧;d1表示R1上的顶点到line2的最小值;d2表示R2上的顶点到line1的最小值; P1表示d1落在line2上的垂足;P2表示d2落在line1上的垂足;ρ0为缓冲区距离;d为有效距离。

1.2.2 缓冲区聚类算法描述

基于共享单车停放点的形状为矩形这一假设，需要的输入数据为待做缓冲区聚类的停放点区域N和待聚类的单车定位数据集S，算法如下：

（1）遍历N，对N的长度和宽度各扩大ρ0，lengthN=lengthN+ρ0，widthN=widthN+ρ0;

（2）m=m+1;

（3）遍历S（p，Xp，Yp），判断点p是否在N内，若属于，则（Xp，Yp）∈Cm;

（4）计算Cm的平均位置做聚类中心C0m，XC0m=，YC0m=;n=n+1;

（5）直到（XC0m，YC0m）不变，S=S-Cm;

（6）结束算法。其中，N为待做缓冲区聚类的停放点区域，N（e，Xe，Ye，length，width，angle），e代表N的编号，Xe代表e的中心点位置的x坐标，Ye代表e的中心点位置的y坐标，length代表e的长度，width代表e的宽度，angle代表e绕（Xe，Ye）逆时针旋转角度;S（p，Xp，Yp）为共享单车定位数据集，p表示单车编号，Xp代表单车p的x坐标，Yp代表单车p的y坐标;聚类结果C（m，Cm），Cm是S中聚成一类的点集;m是聚类编号（初始值m=0）;聚类结果中心C0（m，XC0m，YC0m），XC0m是C0m的x坐标，YC0m是C0m的y坐标;迭代次数n，初始n=0。

1.2.3 混合聚类算法描述

基于共享单车停放点的形状为矩形这一假设，设置K-MEANS聚类的k值为现有停放点数量，需要的输入数据为现有停放点区域数据M和待聚类的单车定位数据集S，算法如下：

（1）统计现有停放区域长度最大值max{lengthM}和宽度最大值max{widthM}，ρ2=√max{lengthM}2+max{widthM}2;ρ1 =0.5ρ2;

（2）计算缓冲区距离ρ0;M的个数为k;

（3）遍历M（e=0），（Xe，Ye）作为初始聚类中心;遍历S（p=0），计算d（（Xp，Yp），（Xe，Ye）），若d（（Xp，Yp），（Xe，Ye））≤ρ1，则（Xp，Yp）∈Cm;

（4）计算Cm的平均位置做聚类中心C0m，XC0m=，YC0m= ;n=n+1;

（5）直到（XC0m，YC0m）不变，S=S-Cm，m=m+1;若m≤k，则进入步骤（3）;否则，进入步骤（6）;

（6）判断S是否为空集，若否，则进入步骤（7）;若是，則进入步骤（12）;

（7）m=m+1;

（8）取S中第一个点（Xp0，Yp0）并将其从S中去除，（Xp0，Yp0）∈Cm;

（9）计算（Xp0，Yp0）与S中其它点集的欧氏距离d（（Xp0，Yp0）， （Xp，Yp）），若d（（Xp0，Yp0）， （Xp，Yp））≤ρ2，则（Xp，Yp）∈Cm;

（10）计算Cm的平均位置做聚类中心C0m，XC0m=，YC0m =;n=n+1;

（11）直到（XC0m，YC0m）不变，S=S-Cm;进入步骤（6）;

（12）计算M中两两之间的距离d（（Xei，Yei），（Xej，Yej）），获得距离矩阵D[d（（Xei，Yei），（Xej，Yej））];

（13）遍历D[d（（Xei，Yei），（Xej，Yej））]，若d（（Xe，Ye），（XM，YM））≤ρ2，则进行缓冲区聚类（算法见上），否则，结束算法。

其中，现有停放点区域数据M（e，Xe，Ye，length，width，angle），e代表M的编号，Xe代表e的中心点位置的x坐标，Ye代表e的中心点位置的y坐标，length代表e的长度，width代表e的宽度，angle代表e绕（Xe，Ye）逆时针旋转角度;共享单车定位数据集S（p，Xp，Yp），p表示单车编号，Xp代表单车p的x坐标，Yp代表单车p的y坐标;聚类结果中心C0（m，XC0m，YC0m），m是聚类编号（初始值m=0），XC0m是C0m的x坐标，YC0m是C0m的y坐标;聚类结果C（m，Cm），Cm是S中聚成一类的点集;聚类距离阈值ρ1和ρ2;缓冲区扩大距离为ρ0;d（i，j）表示点对象i与点对象j的欧氏距离;D[d（i，j）]表示点对象之间的距离矩阵;迭代次数n，初始n=0。

1.2.4 共享单车停放点位置合理性判断流程

判断共享单车停放点位置合理性分为两大步：（1）对单车定位数据进行聚类分析，获得聚类结果;（2）以聚类结果为依据对现有停放点位置合理性进行判断。具体流程图如图2所示。

2 程序实现

2.1 数据说明

借助python生成了142条具有位置信息的共享单车模拟数据和6条具有中心位置信息和长宽信息的现有停放点（矩形）模拟数据。

对单车定位与停放区域模拟数据做可视化，如图3所示，点表示为单车定位数据，方块表示为现有的停放区域数据。

2.2 结果分析

2.2.1 聚类

经过34次迭代后得到单车数据初始聚类结果，如图4所示，其中用圆圈标记的是相邻现有停放区的中心位置，此种情况视为可能会出现聚类结果不理想的情况，需要进一步进行缓冲区聚类。

经过缓冲区聚类后的结果如图5所示，相比较初始聚类结果，原来聚为三类的经缓冲区聚类后聚成了两类，且聚类结果中的元素发生了变动。两类之间有明显的分割线，这条分割线的现实代表可能是一条狭窄的马路，从聚类结果可看出单车数据被很好的分类了。

2.2.2 判断

依据最终聚类结果对现有停放区域的位置合理性做判断，调整结果如图6所示，深色区域对应的聚类中心与现有停放区的中心位置相差无几，但是聚类结果中的元素数量太少，因此判断是要取消施划的停放区域;浅色区域对应的聚类中心与现有停放区的中心位置相差无几，聚类结果中的元素数量多，因此判断是保留不动的停放区域;叉点记号缺少对应的现有停放区，聚类结果中的元素数量多，因此判断是要新增的停放区域。

3 结语

本文提出的混合聚类算法，较为针对性的解决了现有停放点区域相邻时所出现的聚类元素错乱的问题，得出的聚类结果较为理想。以此为依据对现有停放区域的位置做调整是较为科学合理的，能够为共享单车规范化管理的良性发展奠定基础，进一步能够促进共享单车生态环境与城市其他生态环境的和谐共处。

参考文献

[1] 黄多巍，散园园.共享单车对城市道路交通的影响及对策[J].城市道桥与防洪，2018，2018（02）：42-43+9.

[2] I.Frade，A.Ribeiro. Bike-sharing stations： A maximal covering location approach[J].Transportation Research Part A，2015，2015（82）：216-227.

[3] 高楹，宋辞，舒华，等.北京市摩拜共享单车汇源时空特征分析及空间调度[J].地球信息科学，2018，20（8）：1123-1138.

[4] 白江龙.基于Spark平台的共享单车骑行分析[D].内蒙古：内蒙古大学，2018.

[5] Yan Pan， Ray Chen Zheng， Jiaxi Zhang， et al. Predicting bike sharing demand using recurrent neural networks[J]. Procedia Computer Science，2019，2019（147）：562-566.

[6] 史豫坤.基于Hadoop的共享单车停放点选址方法的研究[D].安徽：安徽理工大学，2018.

[7] 索源.基于出行需求波动的共享单车停放点选址规划研究[D].北京：北京交通大学，2018.

[8] 郝洪星，朱玉全，陈耿，等.基于划分和层次的混合动态聚类算法[J].计算机应用研究，2011，28（1）：51-53.

[9] 陶莹，杨锋，刘洋，等.K均值聚类算法的研究与优化[J].计算机技术与发展，2018，28（06）：90-92.

[10] 徐锋.基于矢量的空间对象缓冲区生成算法[C]//广西测绘学会：全国测绘科技信息网中南分网第三十次学术信息交流会论文集.广西：广西人民出版社，2016：523-525.