考虑推进器失效的深海工程船舶动力定位数值模拟

骆寒冰1， 舒德健1， 谢 芃1， 樊 鹤， 于文太

(1.天津大学 船舶与海洋工程系， 天津 300072； 2.海洋石油工程股份有限公司， 天津 300452)

0 引 言

随着我国南海深水油气资源的开发，动力定位技术越来越引起工程和科研人员的重视。动力定位是一种闭环控制系统，利用推进器产生推力来抵抗船舶受到的风、浪、流等外部海洋环境载荷，从而使船舶在指定位置附近运动。相对于传统锚泊定位，动力定位有不受深海水深条件限制、无需布置系泊系统、加快施工进度、降低时间成本等优点。

动力定位系统的关键技术之一是对控制器算法的研究。经过长期研究，目前已经发展出了多种控制算法，比例-积分-微分(Proportion Integration Differentiation， PID)控制器在船舶动力定位中较早出现和发展，其由比例项、微分项、积分项组成，通常联合低通滤波器得到船舶的低频运动来控制船舶运动。BALCHEN等[1]结合卡尔曼滤波改进线性二次高斯分布(Linear Quadratic Gaussian， LQG)算法并用于动力定位控制系统。SΦRENSEN等[2]在模型控制试验基础上，提出新的改进LQG方法用于动力定位船舶。FOSSEN等[3]研究非线性动力定位观测系统以解决系统的稳定性问题，并应用于实船。TANNURI等[4]通过试验分析验证非线性滑移控制算法对动力定位船舶的有效性。边信黔等[5]和赵大威等[6]对动力定位船舶和水下机器人的非线性控制器算法开展研究。刘正锋等[7]分析某油船的动力定位控制能力，并进行模型试验。王德军[8]采用PID算法，分别利用非耦合和耦合方法实现对铺管船动力定位性能分析。孙丽萍等[9]将PID与卡尔曼滤波结合进行全耦合S型铺管船时域分析。高红梅[10]采用模糊PID和PID-DMC控制算法对铺管船进行仿真和对比分析。李勇跃等[11]从平台作业要求定位精度和低能耗角度出发，分析平台动力定位最优方向问题。XIE等[12]对某动力定位深水工程船在斜浪下的运动响应和定位能力进行数值模拟研究。在多种控制器中，PID控制器由于其简单、高效、稳健性强等优点，被广泛应用于各种海洋工程船舶。

本文研究一套工程实用的动力定位数值模拟方法，采用PID控制器并对其控制参数开发整定程序，选用非线性优化方法进行推力分配，利用SIMO求解船舶运动方程，从而实现动力定位船舶的控制。针对某深海工程船舶，开展动力定位数值模拟工作，考虑推进器转角限制以及推进器失效工况，更加接近实际工程情况，可为今后动力定位系统的设计提供参考。

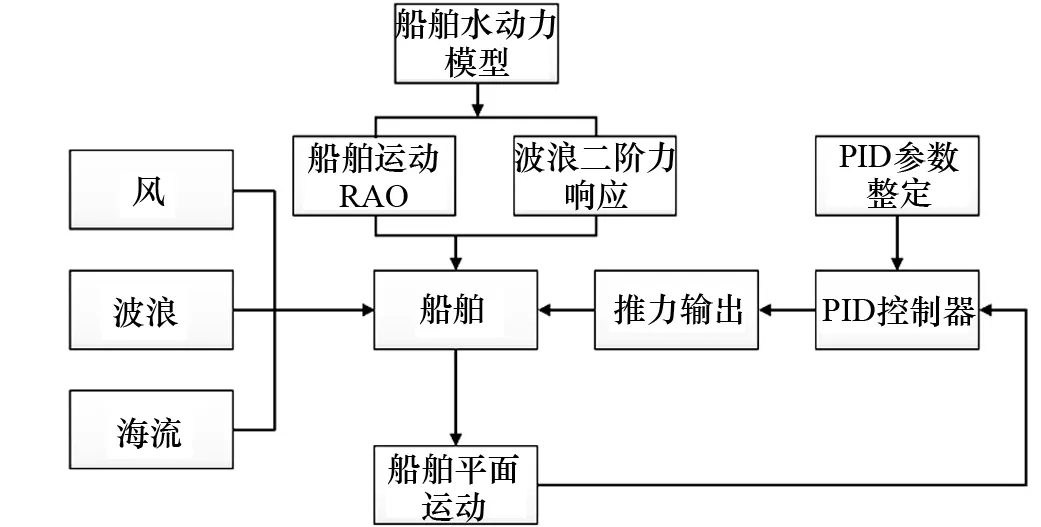
图1 船舶动力定位模拟流程

1 动力定位数值模拟方法

进行船舶动力定位的数值模拟首先需分析船舶受到的风、浪、流等载荷，然后控制系统根据偏差控制推进器输出推力，再将所有载荷加载至船舶运动方程上，最终形成闭环控制，以达到模拟动力定位的目的。具体流程如图1所示。

1.1 动力定位船舶运动方程

动力定位船舶的运动方程[13]为

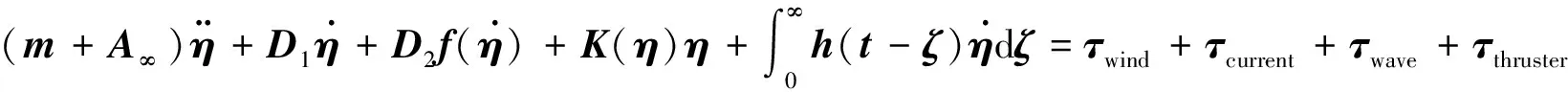
(1)

1.2 PID控制算法

船舶动力定位的控制器是船舶动力定位的关键。PID控制算法为

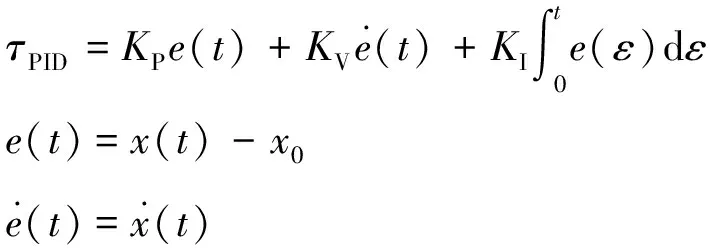
(2)

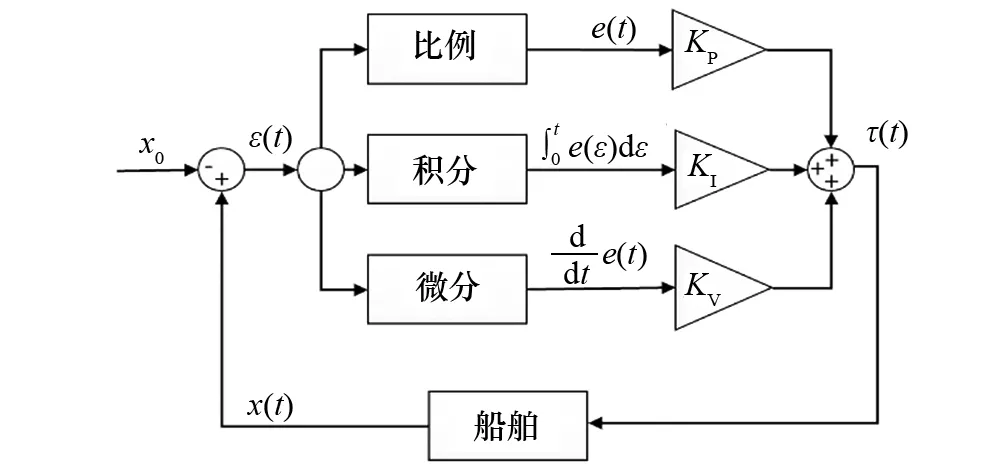
图2 PID控制器控制过程

图3 PID控制参数整定过程

为达到预期的控制效果，需合理选择上述参数，这个过程称为PID控制器的参数整定，采用MATLAB/Simulink开发相应的参数整定程序，在Simulink中建立和模拟完整的动力定位船舶控制系统。图3为整定程序的流程，输入船舶参数和环境载荷，就可以模拟动力定位船舶的PID控制系统，进而得到各参数。利用该整定程序可高效稳定地整定PID控制器的参数，进而有效地模拟船舶动力定位过程。

1.3 推力分配算法

PID控制算法结合推力分配算法可实现推力的控制和分配。通过计算目标函数的最小值，可确定推力大小和推进器角度。定义目标函数Q为

(3)

式中：Fmax为对应推进器最大推力；E为推进器效率；W为权重因数；α为在局部坐标系下推进器的角度；i为推进器编号。在计算目标函数过程中，各推进器的推力与动力定位所需合力的关系为

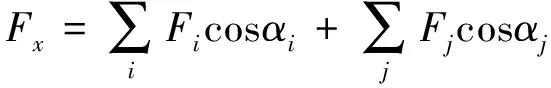
(4)

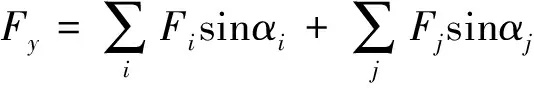
(5)

(6)

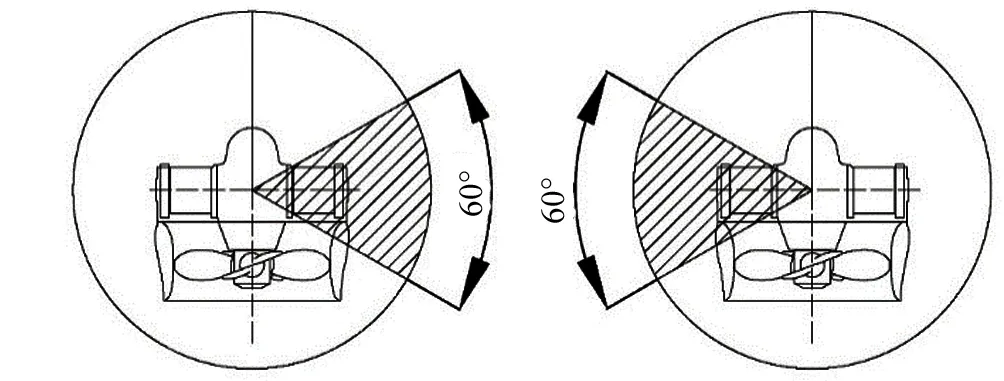
图4 船舶主推进器角度限制

式(4)～式(6)中：Fx为x方向所需推力；Fy为y方向所需推力；M为z轴上所需弯矩；xi和yi为推进器在局部坐标系下的坐标；i为全回转推进器编号；j为固定推进器编号。

当两个推进器距离较近时，某一推进器的尾流可能会对另一个推进器的进速造成影响，导致推力急剧下降，因此需限制推进器的角度变化，如图4所示。每一个推进器的推力都不会超过其额定最大推力。如果某一推进器失效，那么该推进器的推力输出为0。在推力分配中，为了达到所需推力，未失效的推进器输出的推力将会增加。在恶劣海况下，船舶输出的总推力可能不会满足定位需要的总推力，此时动力定位能力就会降低。

2 动力定位深海工程船舶模型

模拟的船舶为“海洋石油286”，其主要功能包括：深水大型结构物的吊装和海底安装，海底深水柔性管敷设，ROV作业支持，海洋工程综合检验、维护和修理，深水锚系处理和锚泊作业等。船舶主尺度如表1所示，其有5个推进器：艉部2个主推进器，艏部2个侧向推进器和1个全回转推进器。推进器布置如图5所示。采用HydroD软件在频域下分析船舶的一阶和二阶波浪水动力。船舶模型网格如图6所示。船舶平面运动RAO、波浪平均漂移力RAO等结果如图7～图12所示。船舶受到的风和流载荷分别如图13和图14所示。

表1 船舶主尺度

图5 船舶推进器布置图 图6 船舶模型网格划分

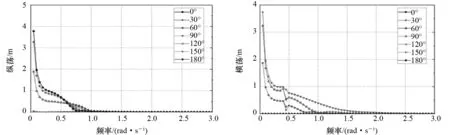
图7 纵荡RAO响应 图8 横荡RAO响应

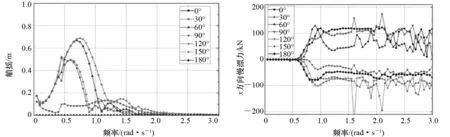
图9 艏摇RAO响应 图10 x方向(纵荡)平均漂移力RAO

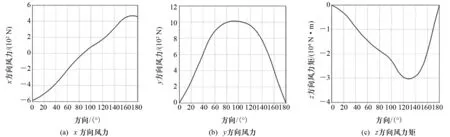
图13 船舶受到风载荷

图14 船舶受到流载荷

3 船舶动力定位时域模拟结果

3.1 模拟海况

该船舶的主要作业海域是我国南海，根据西北太平洋波浪资料统计集[15]选择工作海区，海况为：风速16.5 m/s，流速1.029 m/s，有义波高Hs2.5 m，跨零周期Tz7 s，浪向30°且波浪、风、流的作用方向相同。考虑推进器完整工况和某一推进器失效工况，假设No.2主推进器失效。不规则波采用JONSWAP谱模拟，风采用NPD风谱模拟。

3.2 船舶运动时域结果

图15为波浪时域曲线，图16～图18分别为纵荡、横荡和艏摇时域曲线，图19为水平运动轨迹，图20～图24为5个推进器推力的时域变化情况。其中，“F2”表示主推进器No.2失效工况，“完整”表示推进器完整工况，图19中半径3 m的圆表示水平运动的范围要求，该区域依据DNV的动力定位船舶入级规范[16]选取。

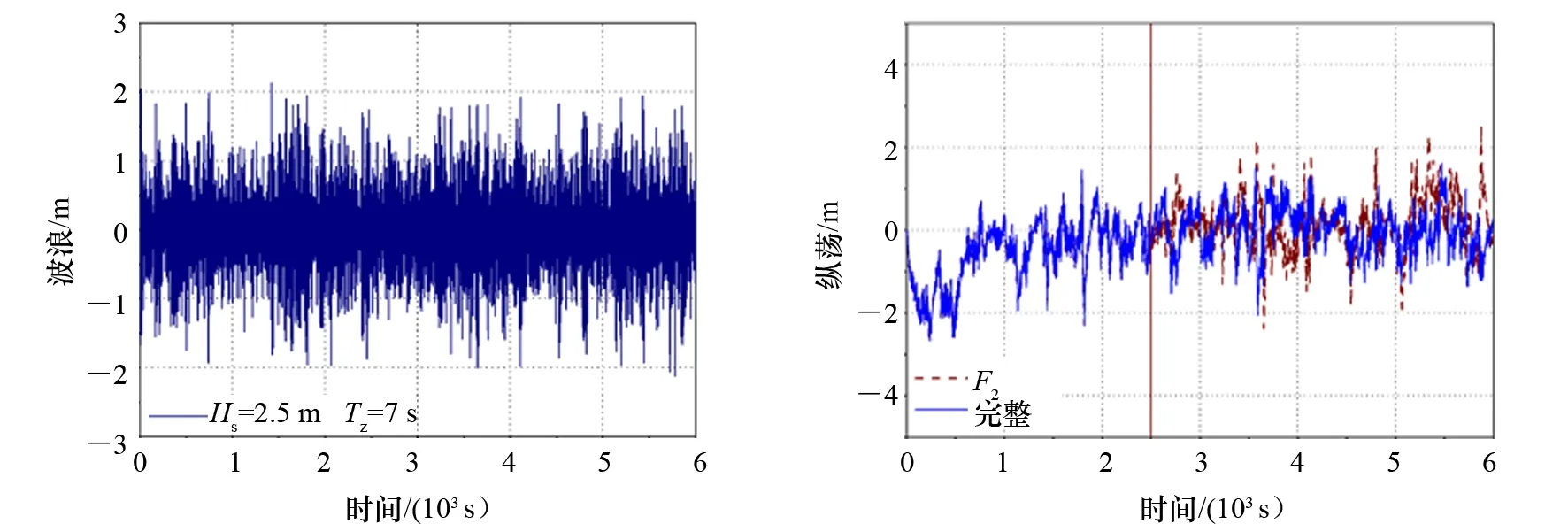
图15 波浪时域曲线 图16 纵荡运动时域曲线

图17 横荡运动时域曲线 图18 艏摇运动时域曲线

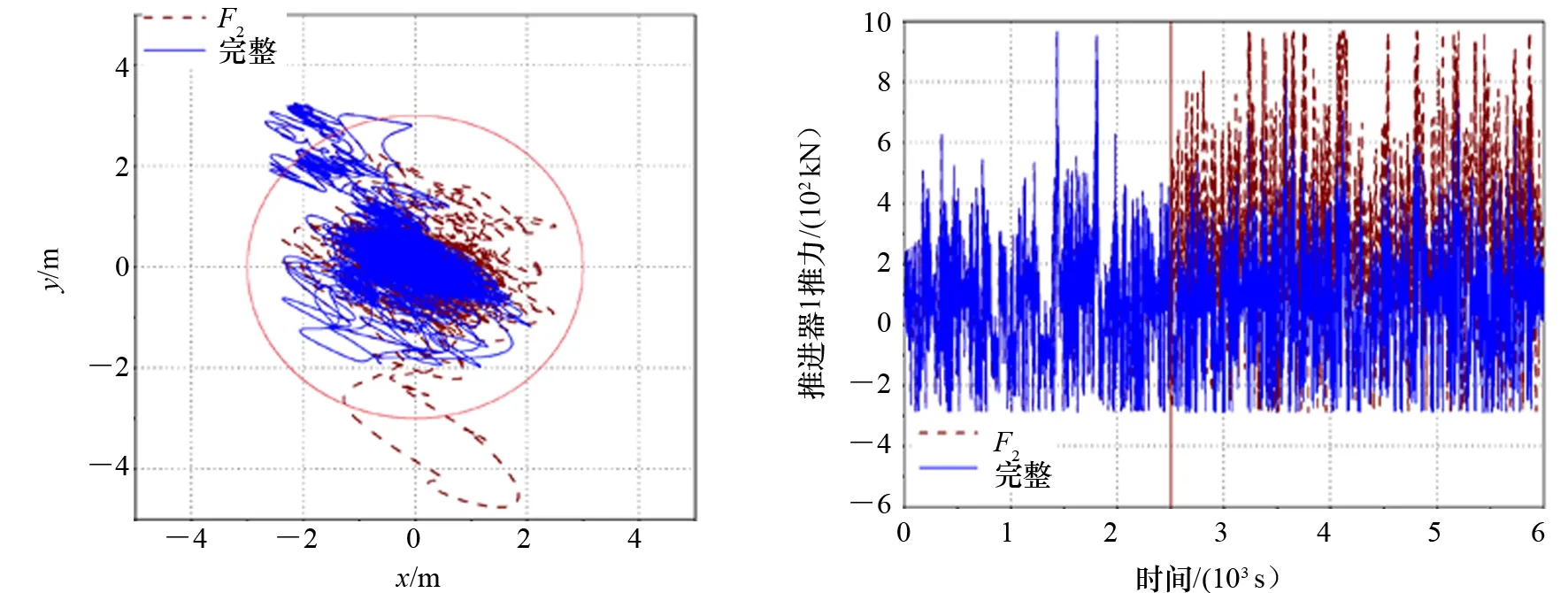
图19 船舶平面运动轨迹 图20 No.1推进器推力输出时域曲线

分析可知：

(1) 推荐算法能够有效预报动力定位船舶在斜浪中的平面运动响应，包括推进器完整以及某一推进器失效工况。

(2) 在推进器完整工况开始的一小段时间内，船舶平面运动部分超出了半径3 m的范围，这是由于PID控制器中的积分在一段时间后才会起作用而使船舶位置逐渐恢复到预定位置。

(3) 在主推进器No.2失效之后，船舶的水平运动响应比原来大，如：在4 100 s左右，船舶横荡运动瞬时幅值达4.71 m，艏摇达13.72°，运动轨迹甚至达5 m圆的范围。

(4) 在主推进器No.2失效后，其推力变为0，为弥补推力损失，其他推进器的推力均相应增大以保持船舶位置。其中，No.1和No.5推进器推力输出增加明显。

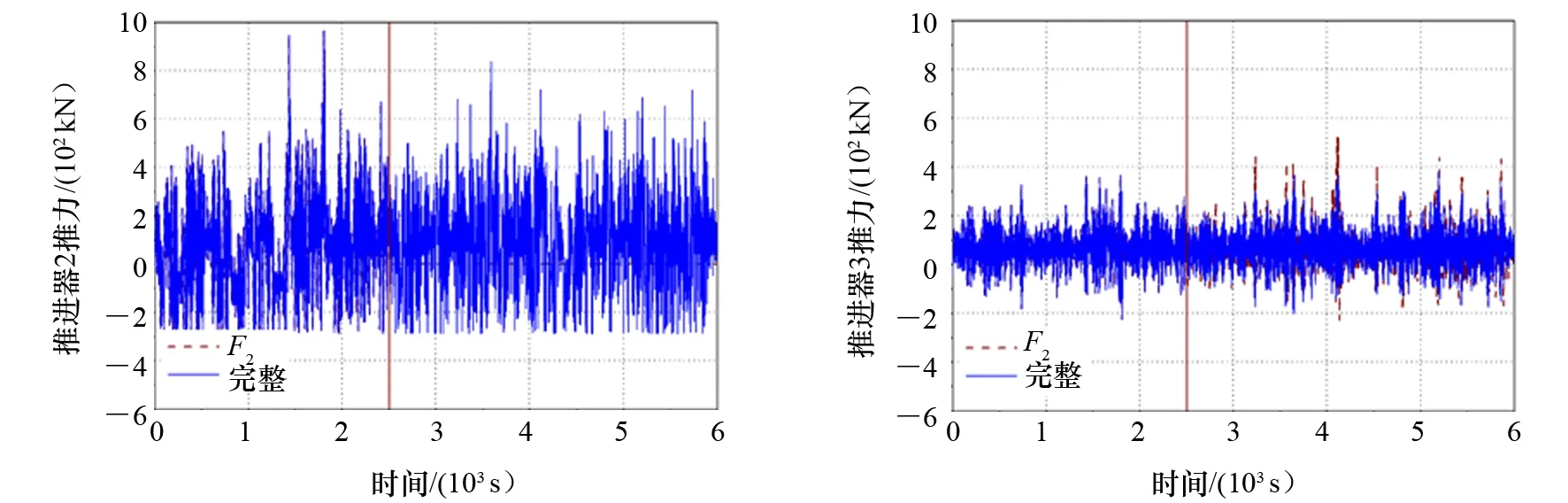
图21 No.2推进器推力输出时域曲线 图22 No.3推进器推力输出时域曲线

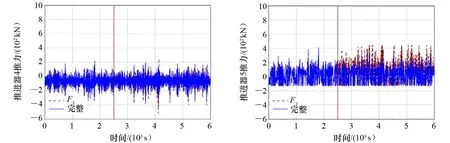
图23 No.4推进器推力输出时域曲线 图24 No.5推进器推力输出时域曲线

3.3 船舶运动频谱分析

对船舶平面运动结果做频谱分析，可以得到运动谱，该谱有两个峰值，分别表示船舶的二阶低频运动和一阶波频响应，经过滤波分析可以得到高频和低频运动统计结果。推进器完整时运动响应的频谱分析结果如图25所示。推进器完整以及主推进器No.2失效时运动谱的滤波分析结果如图26所示。

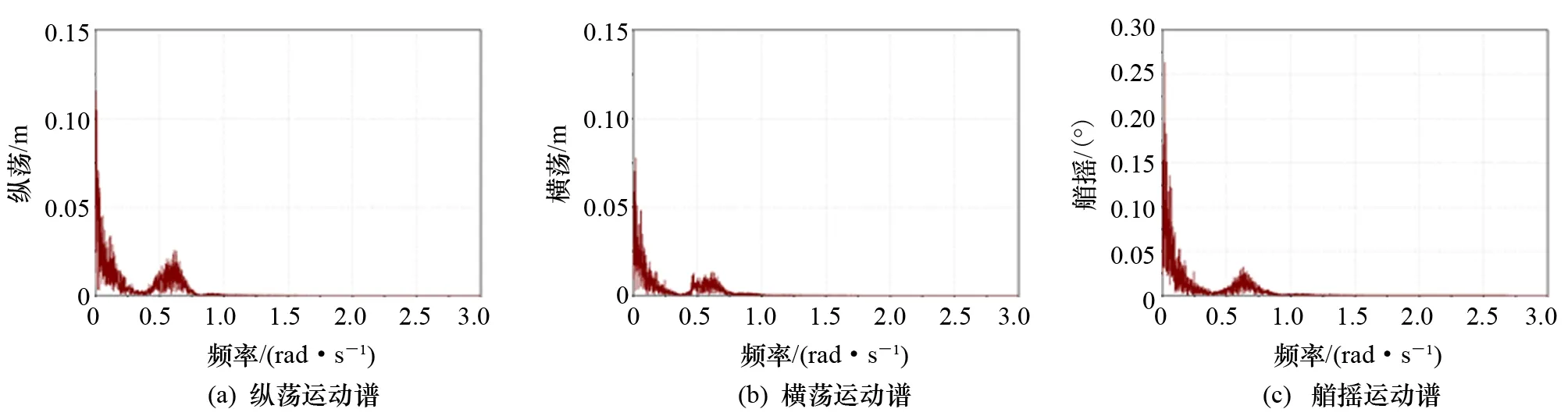
图25 推进器完整时运动谱

图26 主推进器No.2失效和推进器完整时运动统计结果

可以看出，在主推进器No.2失效时，波频响应基本没有变化，而低频响应有所增加，表明主推进器No.2失效对低频运动的控制能力和定位精度有所下降，此时船舶平面运动响应也比推进器完整时大，这是因为动力定位控制的主要是船舶水平运动的低频部分，而对波频部分的影响可以忽略。

4 结 论

研究基于PID控制算法的动力定位数值模拟方法，开发PID控制参数整定程序，采用非线性最优化推力分配策略，利用SIMO求解船舶运动方程，实现对动力定位系统的模拟。采用HydroD预报船舶波浪力，也可采用其他软件预报的水动力结果，适用性好；采用OCIMF推荐的方法计算风和流载荷；考虑推进器角度限制以及推进器失效工况，更接近实际工程情况。针对某深海工程船舶，在风、浪、流组合海况下开展动力定位数值模拟工作。对典型海况下的船舶平面运动进行时域和频域分析，讨论推进器完整以及某一推进器失效对船舶平面运动响应及其定位能力的影响。研究结果表明，该方法可有效地预报动力定位船舶在推进器完整工况和某一推进器失效工况下的动力定位性能，可为船舶动力定位系统的开发和设计提供技术参考。