基于滑模变结构的六相永磁同步电机容错控制

沈雪 朱建光

摘要：該文针对PI控制器有超调问题，将六相永磁同步电机容错控制系统与滑模策略（SMC）相结合，引入新型趋近律，重新设计速度控制器，仿真结果表明SMC控制器优于PI控制器。

关键词：六相PMSM;容错控制;PI控制;SMC

中图分类号：TP273        文献标识码：A

文章编号：1009-3044（2019）22-0254-02

开放科学（资源服务）标识码（OSID）：

Fault Tolerant Control of Six-Phase Permanent Magnet Synchronous Motor Based on SMC

SHEN Xue，ZHU Jian-guang

（Shenyang University of Technology， Shenyang 110870， China）

Abstract：In this paper， the PI controller has an overshoot problem. The six-phase permanent magnet synchronous motor fault-tolerant control system is combined with the sliding mode strategy （SMC） to introduce a new approach law and redesign the speed controller. The simulation results show that the SMC controller is better than the PI controller.

Key words：Six-phase PMSM; fault-tolerant control; PI control; SMC

多相电机的容错控制技术逐渐变得成熟，容错的目的是为故障提供解决方案，最大程度上削减由于故障所造成的损失。工业控制中广泛使用传统的PI控制器，但外部干扰和系统参数的变化会对其造成极大影响。滑模控制（SMC）的快速性和鲁棒性，使与其他众多的智能控制算法相比，具有一定的优越性。

本文在采用一种新型趋近律设计了滑模速度控制器，将滑模变结构控制应用于六相PMSM容错控制系统中，以进一步提高六相永磁同步电机容错系统的鲁棒性。

1 六相PMSM故障后的容错补偿控制原理

六相PMSM容错控制策略是保持故障前定子绕组合成的磁动势与故障后剩余相合成的磁动势相等，经调整剩余各相电流的幅值和相位的大小，以弥补因为缺相所造成的磁动势损失[1][2]。因此，在六相PMSM发生缺相故障后补偿剩余相电流的幅值和相位，使电机在故障后仍然能够形成圆形磁动势，以此来达到电机在缺相后持续运行的目的。

假设六相永磁同步电机的非正交两相定子绕组出现开路故障，本文以C、F两相绕组为例，记剩余定子绕组A、D、B、E四相绕组电流分别为[i′A、i′D、i′B、i′E]，容错电流表达式为[3]：

[i′A=3.46imcosωt-90°i′D=3.46imcosωt+60°i′B=3.46imcosωt+90°i′E=3.46imcosωt-240°iC=0iF=0]                   （1）

2 趋近律的引入

在容错控制基础上，采用一种新型趋近律[4]，如（2）式：

[s=-εf（s）sign（s）-ksf（s）=11-δe-asb+δ]其中[0<δ<1a>0，b>0b∈N]           （2）

式中：[s]表示切换函数，[-εsign（s）]表示等速趋近项，[-ks]表示纯指数趋近项。

采用新型趋近律后可根据系统状态点距离滑模面的远近去调节趋近速度。系统状态点距滑模面远则提高趋近速度，反之则降低趋近速度。

3 滑模速度控制器的设计

在id=0的矢量控制下，六相PMSM的运动方程和转矩方程简化如下：

[Te-TL-Bω=Jdωdt＼Te=3npiqψf]                 （4）

式中：[ψf]为永磁体磁链，[TL]为负载转矩，[B]为阻尼系数，[J]为转动惯量，[ω]为机械角速度。

将系统反馈回来的转速与设定的转速的差即转速误差为系统的输入变量。定义六相电机系统的状态变量：

[x1=ω*-ωx2=x1=-ω]              （5）

式中[ω*]为设定转速值，[ω]为反馈回来的实际转速值。

将式（4）和式（5）联立有（阻尼系数近似为0）：

[x1=-ω=-1J3npψfiq-TLx2=-ω=-3npψfiqJ]            （6）

令[A=3npψfiqJ]   [U=diqdt]，则系统的空间状态方程为：

[x1x2=0100x1x2+0-AU]        （7）

为使系统动态品质良好，无超调的进入滑模面，故选择一阶线性滑模面[s=cx1+x2]，对其求导则有[s=cx1+x2=cx2-AU]，采用前面所述的新型趋近律则有：

[U=1Acx2-siq=1Acx2+εfssigns+ksdt]            （8）

上式中积分器主要对控制量起到滤波作用，进而十分有效地消除了容错控制系统的稳态误差，有效地抑制了抖振，进一步提高了六相PMSM容错系统的动态品质。

4 仿真验证及分析

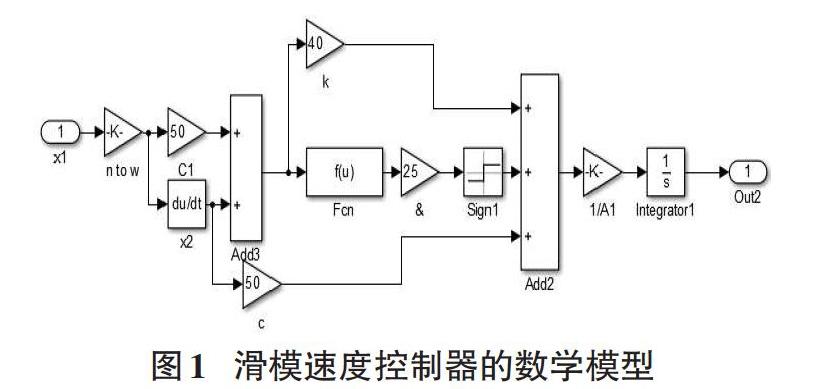
在MATLAB中建立了滑模速度控制器的数学模型如图1所示。当电机正常运行时采取PWM调制;当电机缺相故障时，采取滞环PWM控制。

与双PI调节的六相永磁电机容错控制系统，进行对比，仿真条件：额定转速值设定为270[rad/s]，仿真时间为0.8s，在0.3s时给电机加入20[N]的负载。在0.4s时将C、F两相人为断开，0.5s采用电流滞环进行补偿。双Y形6相PMSM容错控制系统的仿真结果如图2～图3。

PI速度控制器和滑模速度控制器下的容错系统的转速波形对比如图2所示，基于SMC的容错系统与PI调节下的容错控制系统相比，无超调量，能更平稳的达到目标转速，动态品质得以改善。SMC与PI控制策略下的电磁转矩波形对比如图3所示。

可知，在电机空载启动和容错后再次达到稳定的过程中，滑模速度控制器下的电磁转矩比PI控制更快地达到稳定且转矩波动小。因此从仿真结果对比可知，在动态性能和抗干扰能力上应用新型趋近律的滑模控制器使容错系统有较强的鲁棒性。

5 结论

采用基于新型趋近律的滑模速度控制器与六相永磁同步电机容错控制系统相结合。在MATLAB/simulink中分别搭建了PI控制和滑模控制的两种不同策略下的六相永磁同步电机容错控制系统，实验结果表明滑模控制器针对有负载干扰的电机模型，它的鲁棒性较强，动态性能更好，使六相永磁电机的容错控制系统得到了更大的提升。

参考文献：

[1] Jen-Ren F，Lipo T A. Disturbance-free operation of a multiphase current-regulated motor drive with an opened phase[J]. IEEE Transactions on Industry Applications， 1994，30（5）：1267-1274.

[2] 周馬山. 基于DSP的多相永磁同步电机矢量控制系统[D].湖南大学，2004.

[3] 欧阳红林.多相永磁同步电动机调速系统控制方法的研究[D].湖南：湖南大学，2005.

[4] 郭小定，柏达，周少武，等. 一种新型趋近律的永磁同步电机滑模控制[J].控制工程，2018，25（10）：1865-1870.

【通联编辑：唐一东】