基于地基激光雷达的植被聚集指数反演方法

耿志伟，薛 伟，王海滨，张华超，，郭德禹

（1.东北林业大学 工程技术学院，黑龙江 哈尔滨 150040；2.白河林业局，吉林省 延边朝鲜族自治州 133000）

植被聚集指数是表征植被冠层元素空间分布特征的重要参数，描述了真实叶片空间分布与理想状态下随机分布的偏离程度[1]。精确估计植被聚集指数，对研究植被生物量、陆地生态系统碳循环等具有重要意义[2]。此外，聚集指数还可以将有效叶面积指数转化为真实叶面积指数，因此也被定义为植被有效叶面积指数与真实叶面积指数之比[3-5]。当叶片随机分布时，聚集指数为1；当叶片聚集分布时，聚集指数小于1；当叶片规则分布时，聚集指数大于1。自然界中大多数叶片呈现聚集分布状态。

目前，获取植被聚集指数的方法主要有仪器实地测量和遥感技术反演。实地测量一般采用TRAC 仪器（Tracing radiation and architecture of canopies，TRAC）和数字半球摄影（Digital hemispheric photography，DHP）。但两者都需在光照条件下工作，TRAC 设备应在阳光直射下进行手动操作[6]，DHP 需设置最佳曝光时间并在漫射光下获取影像[7]。传统光学遥感反演植被聚集指数的方法多采用中高空间分辨率遥感影像（MODIS、TM 影像）和多角度多光谱数据（POLDER、MISR 数据）[8-9]。然而由于影像热点和冷点易受植被各向异性、太阳角度等因素影响，聚集指数估算具有较大不确定性，因此该技术常用于全球或区域尺度的聚集指数粗略计算[10]。

相比之下，激光雷达（Light detection and ranging,LiDAR）受天气影响小，可快速精准获取植被三维结构信息，已广泛应用于植被结构参数反演[11]。针对星载激光雷达，Yang 等[12]联合中分辨率遥感影像提出了植被冠间聚集指数物理反演方法。针对机载激光雷达，Thomas 等[13]利用地面实测聚集指数和机载点云数据提取的几何参量建立经验模型；Hu 等[14]引入路径长度分布函数表征树冠形状，建立了基于机载激光雷达的聚集指数反演模型。然而，星载激光雷达全波形数据无法直接提供大光斑内地物的精细分布，机载激光雷达聚集指数提取精度极易受点云密度影响。

与星载、机载激光雷达相比，地基激光雷达（Terrestrial laser scanning,TLS）具有空间分辨率高、光斑尺寸小等特点，能够精确刻画植被三维结构，已成为提取植被聚集指数的重要手段[15-22]。现有地基激光雷达反演植被聚集指数的方法可分为三类：一是基于二维图像的强度法。如Zhao 等[16]将激光雷达强度数据通过半球投影生成强度图像，并应用于植被聚集指数提取。二是基于三维体素的几何法。通常将激光点云按照一定规则划分为规则体素获取其间隙率，并假设体素内的点云均匀分布[17-20]。然而，聚集指数反演精度和效率与规则体素的划分方法有关，如何依据叶片特征、点云密度等来选取最优体素仍是该方法的一大难点。如Zheng 等[19]提出径向半球面切片法进行体素划分，较好地实现了冠层间隙率的提取；在此基础上，Ma 等[20]分别探讨了径向半球面切片法、定向切片法等体素划分方法在聚集指数反演中的优劣，并结合间隙大小分布理论实现样方尺度聚集指数反演。三是基于点的几何法，常见于单木聚集指数估算研究[21-23]。如Yun 等[21]基于地基点云数据建立三角网模型，通过识别叶片点来计算冠层真实叶面积指数；Li 等[22]结合激光点云的多回波信息与领域连通法提取冠层间隙，利用间隙大小分步法实现了针对单站地基扫描的植被聚集指数快速提取。

相较而言，基于点的几何法对点云信息的利用较为充足，减少了资源浪费。然而，现阶段基于点的地基激光雷达聚集指数反演研究相对较少。因此，本研究提出了一种利用多站地TLS 数据反演植被聚集指数的方法——基于三维间隙的聚集指数提取方法。该方法利用TLS 获得的点云数据构建Delaunay 四面体格网模型，通过计算四面体体积统计得到三维间隙累积分布函数，最后采用间隙大小分布法反演得到植被冠层聚集指数。该方法相比基于二维间隙的方法更能反映植被的空间聚集特征。同时多站TLS 数据保证了植被聚集指数的高精度提取，为地基激光雷达提取样方尺度植被聚集指数提供一种新思路。

1 数据获取

本研究收集了位于内蒙古根河林区（38°29′N～38°59′ N，100°12′ E～100°20′ E）和甘肃张掖林区（50°01′ N～50°51′ N，121°20′ E～121°38′ E）的20 块30 m×30 m 植被样方的地基激光雷达数据和野外实测验证数据（图1）。2 个林区的地面实验分别在2016年8月和2012年7月展开。各样方内植被茂密，死树较少，地势相对平坦。

1.1 地基激光雷达数据

2 个林区使用的地面激光扫描仪都为RIEGL VZ-1000。最大脉冲频率和射程分别为300 kHz 和1 400 m，测距精度为2 mm@50 m 处。仪器架设高度约为1.8 m，扫描视野为360°×100°。为减少枝叶遮挡效应、精确获取冠层完整结构，本研究对每个样地均进行5 个测站的扫描（图2）。同时在每个样方中布设6 个固定黑白标靶，方便在后续操作中将各测站数据统一在一个坐标系下。样方中心测站能够看到所有标靶，其余测站至少扫描3 个标靶。地基激光扫描在清空无风的条件下进行。

1.2 野外实测数据

图1 研究区域 Fig.1 The position of the study area

地面实测在地基扫描样方中同步开展，测量方式为TRAC 仪器。测量在晴朗无云条件下开展，且太阳光较为稳定。操作人员手持仪器以约0.3 m/s速度匀速前进，行走方向垂直于太阳入射方向，每个样地进行150～200 m 样线采集（图2）。

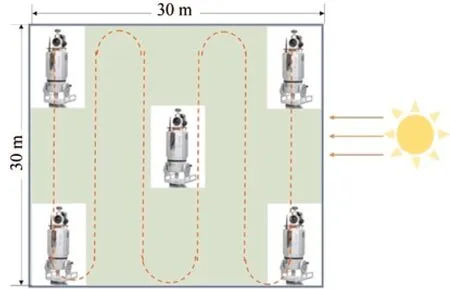
图2 样方扫描基站分布及TRAC 测量样线（红色虚线）Fig.2 The distribution of scan positions and TRAC sampling line (red dotted line)

2 植被聚集指数提取方法

本研究通过地基激光扫描数据预处理、植被点云提取、四面体格网模型建立、间隙累积分布函数计算、间隙大小分布法等过程实现植被冠层聚集指数的反演，具体流程如图3所示。

2.1 点云数据预处理

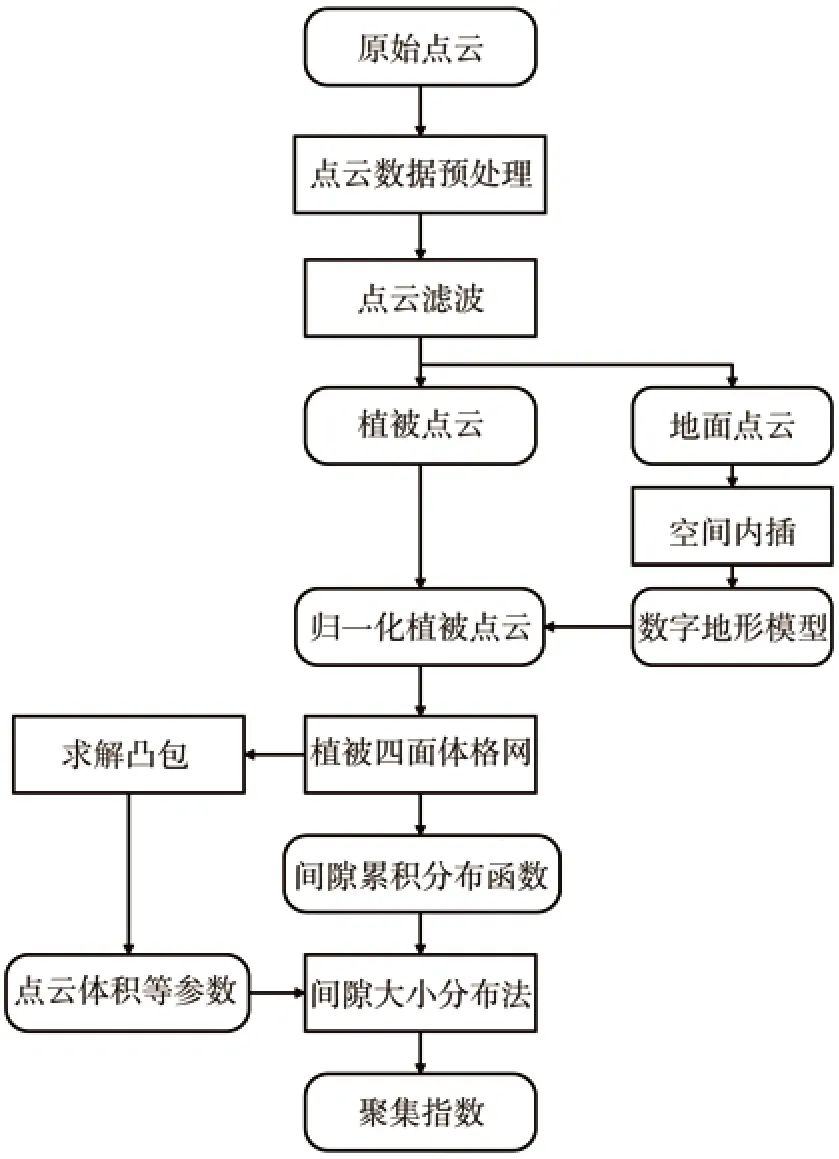
图3 植被聚集指数反演技术流程Fig.3 Workflow diagram for clumping index retrieval

TLS 点云数据预处理工作主要包括点云配准和点云去噪。点云配准的目的是将多站地基数据转换到同一坐标系下，得到目标整体数据集。本研究选用基于公共标靶的配准方法，将标靶中心作为两个测站数据的公共点，通过自动添加约束条件实现基于标靶的配准。该方法与手工选取同名特征点的拼接方法相比，精度高且效率快。最终20 个样地的配准误差均不超过3 mm，满足后续实验精度要求。然而，受系统误差、环境干扰等影响，配准后的点云数据中仍存在明显噪声。因此，本文采用基于局部空间统计的去噪算法对配准后点云进行处理。该方法将局部点密度与整体点密度相差较大的点标记为噪声点，实现噪声去除，在保留目标有效细节特征的同时，保证了点云数据密度相对均匀。

2.2 植被点云提取

由于研究对象为植被点云，因此采用Zhang等[24]提出的布料模拟滤波算法实现地面信号与植被信号的快速精确分离。具体实现过程为：首先将整体点云进行反置，随后将一块刚性布料覆盖在翻转后的表面上；模拟布料在重力作用下的下落过程，确定布料节点的位置，即地形表面位置；最终对比地形表面和原始点云，分离地面点云与植被点云。

基于滤波获得的地面点云，使用一次样条有限元法进行空间内插[25]，建立空间分辨率为0.2 m 的数字地形模型（Digital elevation model,DEM）。之后，将点云滤波后得到的植被点云以X、Y坐标为依据，根据生成的DEM 影像分辨率尺寸划分到不同格网。将落在格网内的植被点高程减去对应的DEM 格网值，即得到归一化植被点云。此时植被点云中的点高度全部转换为其相对地面的高程，即植被高度。

2.3 四面体格网模型构建

为获取植被冠层的间隙累计分布函数，本文提出通过构建Delaunay 四面体格网模型来对植被点云进行处理。四面体格网模型能够保留原始点云数据，同时精确表达植被与间隙的空间分布。但常用的构网方法普遍存在效率低、速度慢等缺点，极其不适用于密度高、数据量大的地基点云数据。因此本研究采用分而治之算法进行四面体格网模型构建。

首先，将所有的植被点云进行虚拟三维规则格网划分，保证每个格网中至少包含一个数据点；并设定格网点云密度阈值判定各格网是否为密集格网。接着，在格网内选取种子点，采用局部优化算法（Local optimization procedure,LOP）[26-27]，即选择最小角最大法连接种子点，建立得到初始四面体。在此基础上依次加入非密集格网内的点，直至所有非密集格网内的点都连接完成（图4）。然后处理数据密集三维格网，先在密集格网内部构建Delaunay 四面体，保证密集格网内部点均被连接，再将新生成的内部Delaunay 四面体与其外部四面体格网进行合并。直至遍历所有密集格网点云数据，形成一个完整四面体网络。最终，构建的四面体格网模型形成了大量小四面体，所有小四面体一起构成植被点云凸包。

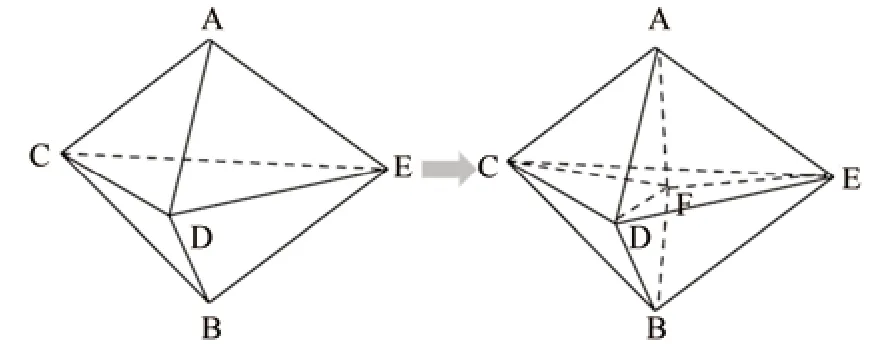
图4 Delaunay 四面体格网生成Fig.4 Delaunay tetrahedral network generation

该四面体格网模型满足：1）网格模型中的每个面均为平面凸三角形；2）网格中每条边有且只有2 个三角形共有；3）三角形组成的四面体之间不存在重叠或遗漏，且不包含植被点云以外的体积。对于任意一个四面体，设点O、A、B、C为其4 个顶点，其三维空间坐标分别为（XO，YO，ZO）、（XA，YA，ZA）、（XB，YB，ZB）、（XC，YC，ZC），则四面体TOABC的体积可计算得到（式（1））。

所有小四面体的体积累加起来即为整个植被点云凸包的体积。将小四面体体积除以凸包体积，统计不同体积的四面体出现的概率，即得到间隙累积分布函数Fm(λ)。该函数定义为体积大于λ的所有间隙所占的比例。

2.4 聚集指数计算

将基于四面体格网模型计算得到的间隙累积分布函数，输入到Chen 和Chair 提出的间隙大小分布法（CC 算法）中[6]，计算得到聚集指数。该方法将叶片随机分布下的间隙累积分布函数与实际分布函数进行对比，经过逐步迭代移除大间隙的方式定量衡量植被聚集效应。对于叶片随机分布的冠层，其间隙累积分布函数为：

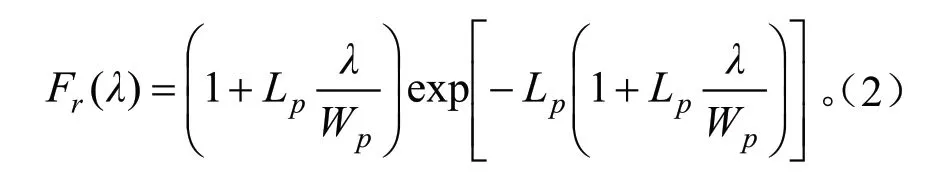
式中：Fr(λ)是随机分布冠层的间隙累积分布函数。Lp是投影叶面积指数，其初值为-ln[Fmr(0)]，其中Fm(0)是实际总间隙率。Wp是叶片投影后的平均宽度，其计算方式为：

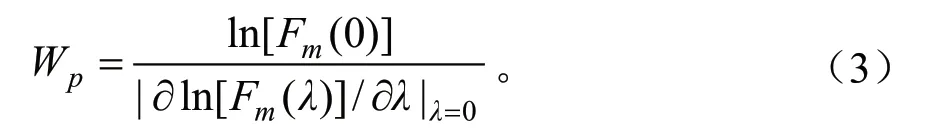
当实际间隙出现概率超过Fr(λ)时，则被认为是非随机大间隙，将其移除。每删除一轮大间隙，重新计算间隙累积分布函数Fmr(λ)，并通过新的-ln[Fmr(0)]计算新的Lp。经多次迭代后，间隙累积分布函数Fmr(λ)将接近随机状态下的间隙累积分布函数。迭代终止条件为Lp增长幅度小于规定阈值，或Fmr(λ)的一部分落到Fr(λ)曲线下面。最终该算法计算得到的聚集指数表达式[28]为：

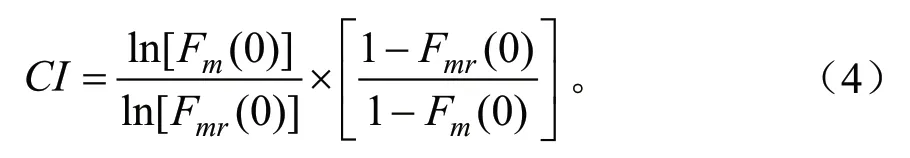
式中：Fm(0)是原始冠层总间隙率，Fmr(0)是大间隙被移除后的冠层总间隙率。

结合四面体格网模型和间隙大小分布法的植被聚集指数反演方法，以三维分布的冠层间隙形式消除了二维间隙样线内部的不均匀性，并通过对比聚集分布和随机分布下三维间隙累积分布函数，最终达到高精度反演植被聚集指数的目的。

3 结果与分析

3.1 点云数据处理

以根河某一样地数据为例，使用布料滤波算法对预处理后点云数据（图5a）进行地面和植被的分离，结果如图5b 所示，红色表示地面点云，绿色代表植被点云。经地面点内插与植被点云相对高程计算，最终得到归一化植被点云，如图5c所示。可以看出，布料滤波实现了复杂地形下地面点和非地面点的精确分离。然而对于植被下层存在的杂乱点，滤波结果仍存在一些误差，这与样方中的低矮植被有关。低矮植被通常生长浓密且分布均一，导致激光脉冲到达地表概率降低。滤波处理时，低矮植被点云可能被判别为地面点，可选择人工修正来进一步处理。此外，由于本文主要研究对象为森林冠层，低矮植被在样方植被中占比较小，且野外TRAC 仪器实测时测量高度一般高于低矮植被高度，因此低矮植被对样方内聚集指数反演精度影响不大。

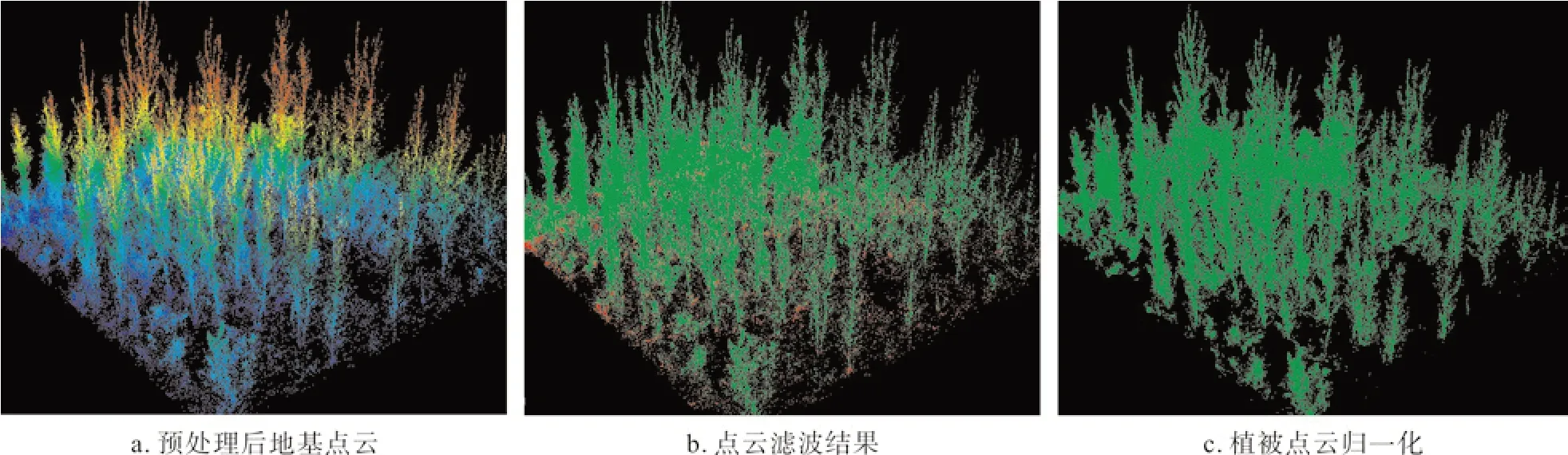
图5 点云数据处理结果Fig.5 TLS point cloud data processing

3.2 植被聚集指数反演

3.2.1 植被点云四面体格网模型

将归一化植被点云划分为三维规则格网（图6a），遍历所有格网内植被点云，构建Delaunay四面体格网模型（图6b）。可明显看出，树冠内的植被点云密集，生成的三角面片极多，四面体体积也相对较小。同时，叶片的聚集分布导致了大间隙的出现，表现为四面体格网模型中较大体积四面体出现的概率增加。利用顶点点云三维坐标计算获得所有小四面体体积，将其累加即为植被点云凸包体积（图6c）。统计不同体积的四面体出现的概率，得到该植被冠层的间隙累积分布函数，如图7所示。

图6 植被点云四面体模型Fig.6 Delaunay tetrahedral network model of vegetation point cloud

本研究采用四面体模型来获取植被三维间隙累积分布函数。传统方法的间隙累计分布函数多基于间隙尺寸，即二维间隙。然而离散激光点云的二维间隙尺寸很难给出明确定义，且计算二维间隙会忽略第三维的聚集特征。因此，本研究得到的间隙累积分布函数更符合三维空间实际情况，为后续聚集指数反演提供了准确的间隙分布参量。

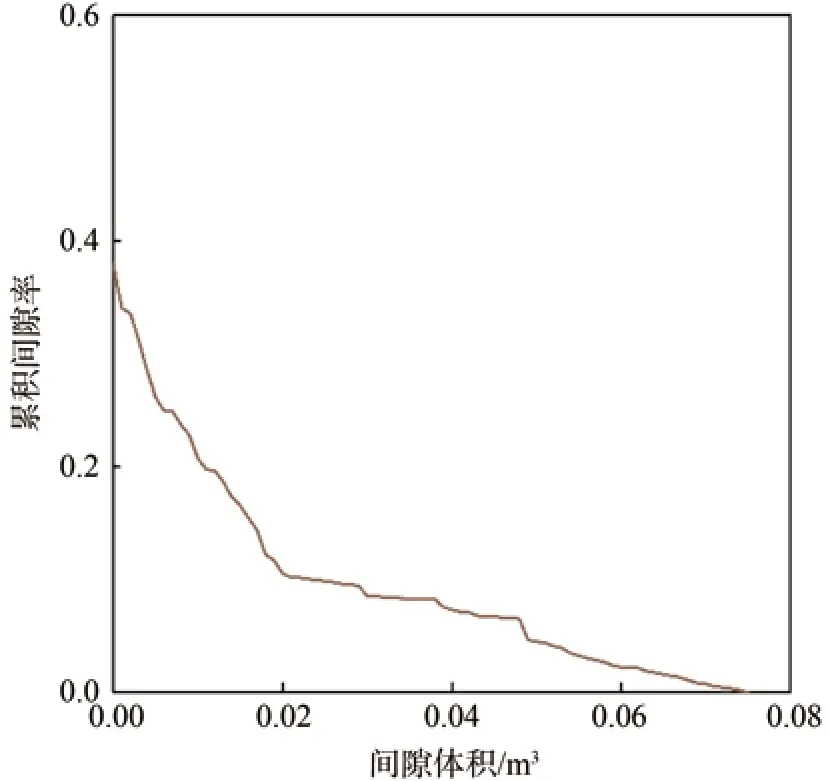
图7 间隙累积分布函数Fig.7 Gap cumulative distribution function

3.2.2 聚集指数反演结果

通过多次迭代移除大间隙的方式，从三维间隙累积分布函数中计算得到植被聚集指数，间隙累积分布函数迭代前后的结果如图8所示。可以看出，与理想随机分布状态相比，实际聚集分布下的植被冠层内大间隙频数明显较多，小间隙频数较少。经多次迭代后，实际间隙累积分布函数与理想场景中几乎吻合，但仍存在一定程度的抖动。这是因为理想随机分布场景下的Fr(λ)是一个光滑曲线，而Fm(λ)是存在锯齿状的实测曲线。即使Fmr(λ)满足迭代终止条件，也不可能与Fr(λ)完全重合。

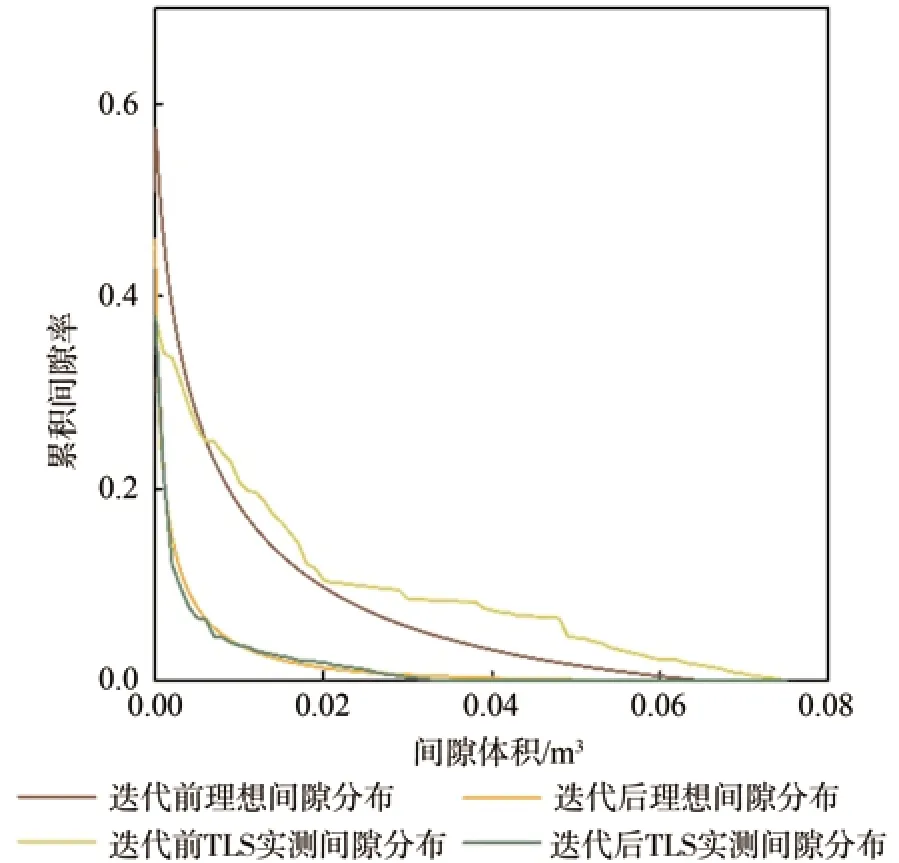
图8 间隙累积分布函数迭代结果Fig.8 Gap cumulative distribution functions before and after iteration

为验证该方法提取植被聚集指数的精度，选取决定系数R2、相对均方根误差rRMSE作为指标，对20 个样方内TLS 数据提取的聚集指数结果进行评价。图9为实测聚集指数与TLS 反演的聚集指数的相关关系图。由图9可得，该方法反演的聚集指数与实测聚集指数表现出较好的正相关性（R2=0.74，rRMSE=8.94%）。然而，由三维间隙计算得到的聚集指数与TRAC 仪器测量值相比，存在略微低估。其原因除了受间隙阈值设置的部分影响外，更主要在于两者原理不同。TRAC 仪器基于观测样线采集的是二维间隙，而多站地基激光雷达通过大量脉冲覆盖整个三维空间。基于四面体模型的三维间隙比二维间隙更能反映出植被的真实聚集情况。由此可推论，目前植被聚集指数实地测量方法得到的测量值仍偏低，与Ryu 等[29]的结论一致。

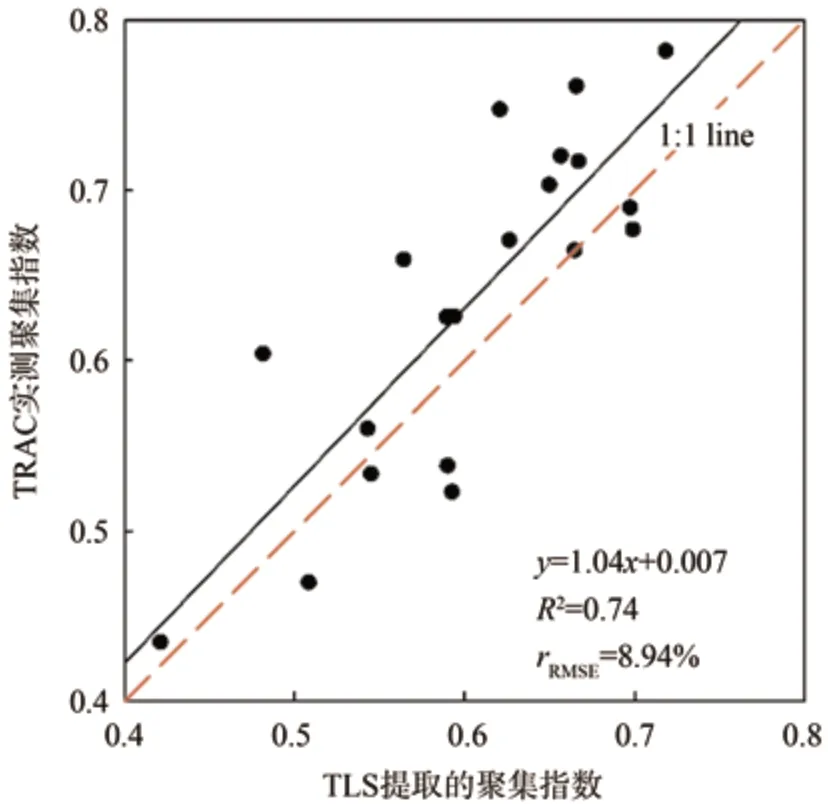
图9 TLS 提取的聚集指数与实测聚集指数相关关系Fig.9 Relationship between the TLS-derived CIs and the TRAC-measured CIs

4 结论与讨论

本研究经多站地基激光雷达扫描，获取了内蒙古根河林区和甘肃张掖林区多个样地点云数据，然后通过数据预处理、植被点云提取、四面体格网模型构建和间隙大小分布法，实现了样方内植被聚集指数反演。主要结论如下：

1）首次提出利用四面体格网模型来获取植被三维间隙，并计算得到植被间隙累积分布函数。该模型充分利用了激光雷达精确获取目标三维信息的能力，得到的间隙累积分布函数也更能体现植被三维结构信息。

2）将四面体格网模型与经典的间隙大小分布法相结合，通过逐步移除大间隙的方式，使得聚集分布的森林冠层逐渐接近随机分布。

3）经TRAC 仪器测量的聚集指数验证，该算法能够较好地提取植被冠层聚集指数（R2=0.74，rRMSE=8.94%，n=20），但存在略微低估，其原因主要为计算原理不同。二者采用的虽然都是间隙大小分步法，但TRAC 仪器利用样线采集得到二维间隙，本文方法采用TLS 点云获取得到三维间隙。

总体而言，本文基于高密度地基激光雷达数据，提出了利用三维间隙反演植被聚集指数的方法，能够更加真实地反映出植被冠层的聚集情况。然而，该方法对数据质量要求较高，要求点云密度相对均匀，且尽量避免目标的前后遮挡。若点云密度相差较大，由低密度处的植被点云生成的四面体极大可能会被标记为三维间隙，导致聚集指数估算不准。因此如何将该方法迁移到存在明显遮挡的单站地基激光雷达或机载激光雷达数据，克服该方法在点云密度不均情况下的局限性，是下一步的研究方向。此外，探讨基于二维间隙与三维间隙提取的聚集指数间的根本差异，也是本研究未来需重点开展的工作。