矿产勘查特高品位样品的识别、剔除和处置方法探讨
2019-10-30张立明魏士书郭帅
张立明,魏士书,郭帅
(安徽省地质矿产勘查局312地质队,安徽蚌埠 233040)
1 关于特高品位
在贵金属和有色金属矿体中,有时出现单样或多样品位大于同一矿体、块段或临近地段平均品位数倍或数十倍的很高的品位,称特高品位或风暴品位。(原国家矿产储量管理局曾对70份有色和贵金属勘探报告统计,有近56%的特高品位下限值,相当于矿体平均品位的10~15 倍之间,其余的为4~9 倍间不同矿种、不同矿床特高品位下限值是不同的,特高品位下限值随品位变化均匀程度而变动,品位变化越均匀,特高品位下限值越小,反之则大。变化幅值为平均品位2~3倍至15倍以上[2]。
从数理统计学角度讲,特高品位是相对于“该数据集”的一些高品位“离群值”,它是混入数据集的另一统计母体的数据。特高品位下限值大小反映了其在数据集中的“离群”程度。要准确描述本数据集的特征,计算其特征参数,就要将这些“离群值”剥离剔除。
特高品位下限值大小,主要决定于样品的品位变化均匀程度,即品位变化系数的大小。品位变化系数越大,特高品位下限值越高,反之则小。而品位变化系数的大小决定于数据集的均方差(标准离差)大小,均方差越大,变化系数越大,反之则小。均方差是刻划数据集离散程度的一个核心特征参数。
矿产勘查对于品位变化的均匀程度,用变化系数表述,因矿种的不同,衡量变化系数数值尺度标准也不一样。现行的部分单矿种地质勘查规范对不同矿种变化系数档次给出了不同的数值尺度(见表1)。
矿产勘查时,要正确、合理的计算平均品位、品位变化系数等。它深刻影响到矿床勘查类型确定、矿体平均品位计算,进而影响矿产资源/储量计算。而正确识别和合理剔除特高品位,是计算平均品位的基础。相关的矿产勘查规范,要求计算平均品位时剔除特高品位,以减少因特高品位对平均品位的影响,减少给矿山开发带来的风险。
从矿床品位变化的实际出发,对特高品位进行合理的判别和技术处理(剔除),是矿产勘查重要环节之一。
2 确定特高品位下限的方法
传统方法主要有:类比法、规范法、计算法(和)、统计法和品位累计频率法等。
2.1 类比法
类比法是根据已勘探矿床的经验数字进行比较,确定特高品位下限。
2.2 规范法
不同矿种勘查规范对各类矿床特高品位最低界限有相应规定,执行规范的规定即规范法。
《岩金矿地质勘查规范》DZ/T0205-2002、《铜、铅、锌、银、镍、钼矿地质勘查规范》DZ/T0214-2002、《钨、锡、汞、锑矿地质勘查规范》DZ/T0201-2002、《砂矿(金属矿产)地质勘查规范》DZ/T0208-2002、《固体矿产勘查地质资料综合整理综合研究技术要求》DZ/T 0079-2015 及《固体矿产勘查工作规范》GB/T 33444-2016等。
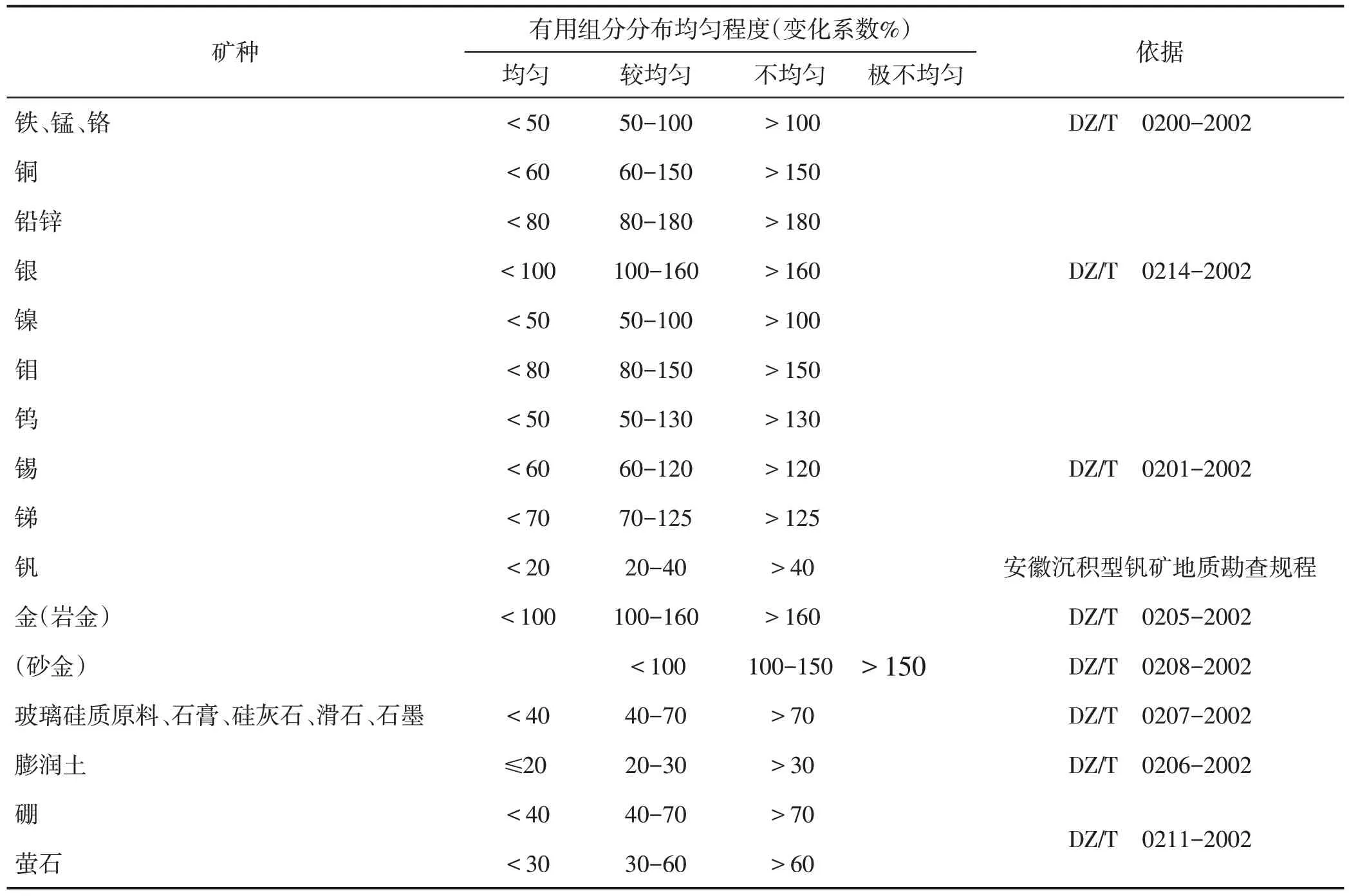
表1 部分地质勘查规范对有用组分分布均匀程度划分表Table 1.Division of distribution uniformity of useful components in some geological exploration specifications
2.3 计算法(影响系数法)
教科书(如《固体矿产勘查技术》杨云保等地质出版社,2007.7)及有关文献介绍了沃洛多莫诺夫提出的下列公式计算特高品位下限:

式中:
Ct-特高品位下限(正常样品品位的上限);
-包括特高品位在内的平均品位;
N-包括特高品位在内的样品数目;
M-特高品位使平均品位增高的百分数。
其中:

用沃洛多莫诺夫公式(1)计算特高品位下限,其实质是包括特高品位在内的平均品位+修正系数。公式(1)中N与特高品位下限Ct成正比,即样品数愈多,特高品位的下限数值愈高。其结果是当样品数很大时,特高品位下限值会很高,公式(1)存在明显的不合理。
2.4 统计法
传统的确定特高品位的方法是建立在经验总结的基础上,所谓平均值的6~8 倍,它没有充分地考虑到各个矿区样品数据集的数理统计特征之差异。如果确定特高品位与矿石组分品位的分布函数关系,那这个函数就能较完整地说明组分(品位)数值的总体性质。知道了样品数据集分布函数的形式之后,可以利用该函数的统计参数、确定小于或大于任一给定值样品品位所出现的概率,并以此概率来确定特高品位的临界值。
一般矿床的品位参数分布形式是正态分布或对数正态分布。它们由品位的平均值和标准差来确定(或品位的对数平均值、对数方差)。在实际工作中,常用正态函数表来计算大于或小于给定值的正态随机变量数值所出现的概率:
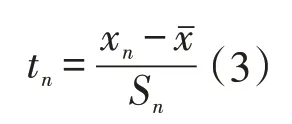
式中:tn——正态分布函数的自变量数;xn——待检测的特高品位值;——样本的算术平均值;Sn——标准差(均方差)。
对数正态分布情况下,tn按下式计算:
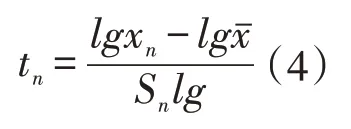
式中:lgxn——待检测的特高品位值的对数;lg——对数的算术平均值;Snlg——品位对数均方差的估值。
计算出tn后,利用正态分布积分函数表查出φ(t)值。按1-φ(t)公式算出大于或等于待检测的特高品位值的出现概率Pn。然后把样品数n×Pn即为特高品位样品个数。
具体操作是首先检查这些高品位值中最小的一个,如果发现这一数值属于特高品位,那么其它的(大的)数值也应属于特高级。
2.5 品位累积频率法
品位累积频率分布曲线97.5%分位数所对应的品位值,即=a+1.96σ(xi=+1.96s)所对应的品位值作为特高品位的下限。
3 讨论
上述确定特高品位下限值的各方法,研讨如下:
(1)类比法和规范法都是经验性的、参考性的,它不能精确的满足各矿床品位变化千差万别的实际情况。因此实际工作中应立足于研究勘查矿床的品位变化实际情况,对特高品位下限予以论证、判别和处置,不能机械地套用。
较多的规范规定了用平均值(含特高品位)6~8倍作为特高品位下限,进行特高品位剔除。它存在不足是:用平均值(含特高品位)6~8倍作为特高品位下限,没有区别特高品位的识别标准和剔除标准。据《数据的统计检验和解释正态样本离群值的判断和处理(GB/T4883-2008)》相关规则,在数据集中,不是所有被检出的离群值都该剔除,部分离群值或是“歧离值”,它是属于本数据集的数据,对它不能剔除;用6~8倍平均值(含特高品位)作为特高品位下限,没有充分顾及勘查矿区实际的矿石品位变化数据分布特征;用6~8倍平均值(含特高品位)作为特高品位下限缺乏现代数理统计方法基础理论支撑,数理统计对数据分布特征的描述,是用平均值(xˉ)刻划数据的集中程度,用标准差(σ)描述数据的离散性。集中性与离散性是两个概念,用集中性来表述离散性显然不妥。因而“平均值的倍数”,不能精确描述品位数据离散特征(特高品位的离群特征)。“平均值的6~8 倍”,只能是一些矿区特高品位的统计结果,是经验性的、浅表性的指标,缺乏精确的数理统计理论指导意义。
(2)计算法中沃洛多莫诺夫公式法给出的公式(公式1),N与特高品位下限Ct成正比,即样品的数目愈多,特高品位的下限数值愈高。当样品数很大时,特高品位的下限值会很高,这时特高品位下限值就失去其意义了。从经验可知,自然界成矿地质作用多期性及成矿背景复杂性,元素的地球化学行为千差万别,使某些矿产的品位变化很大,从而形成一些离群的高品位值(特高品位)。矿体中的特高品位的存在是客观现实,不会因采样数量增加而消失。“特高品位下限值随样品数加大而增高”这个关系式不够合理,因此公式(1)不适用特高品位下限的判别。
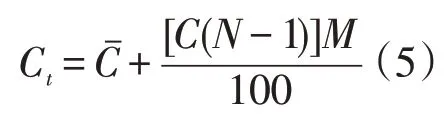
修正后的公式相对合理。
但此公式(式5)是平均值加影响系数作为特高品位下限值,并没有揭示特高品位的离散特征,其内在的函数关系尚待进一步研讨。
(3)特高品位的识别水平和剔除标准应予区分。地质统计学常用品位累积频率97.5%,即x=a+1.96σ(用实验数据时表述为)所对应的品位作为特高品位的下限值即剔除标准。据《数据的统计检验和解释正态样本离群值的判断和处理(GB/T 4883-2008)》相关规则:品位累积频率97.5%这个尺度所认定的品位高值,只能作为离群值的识别水平而不能作为剔除标准。剔除标准要用F(x)=99%,相当于x=a+2.33σ相对应的品位值,即99%水平或2.33σ水平。地球化学勘查中数据的高含量值剔除标准(DZ/T0145-2017)是x=a+3σ相对应的元素含量。见表4。
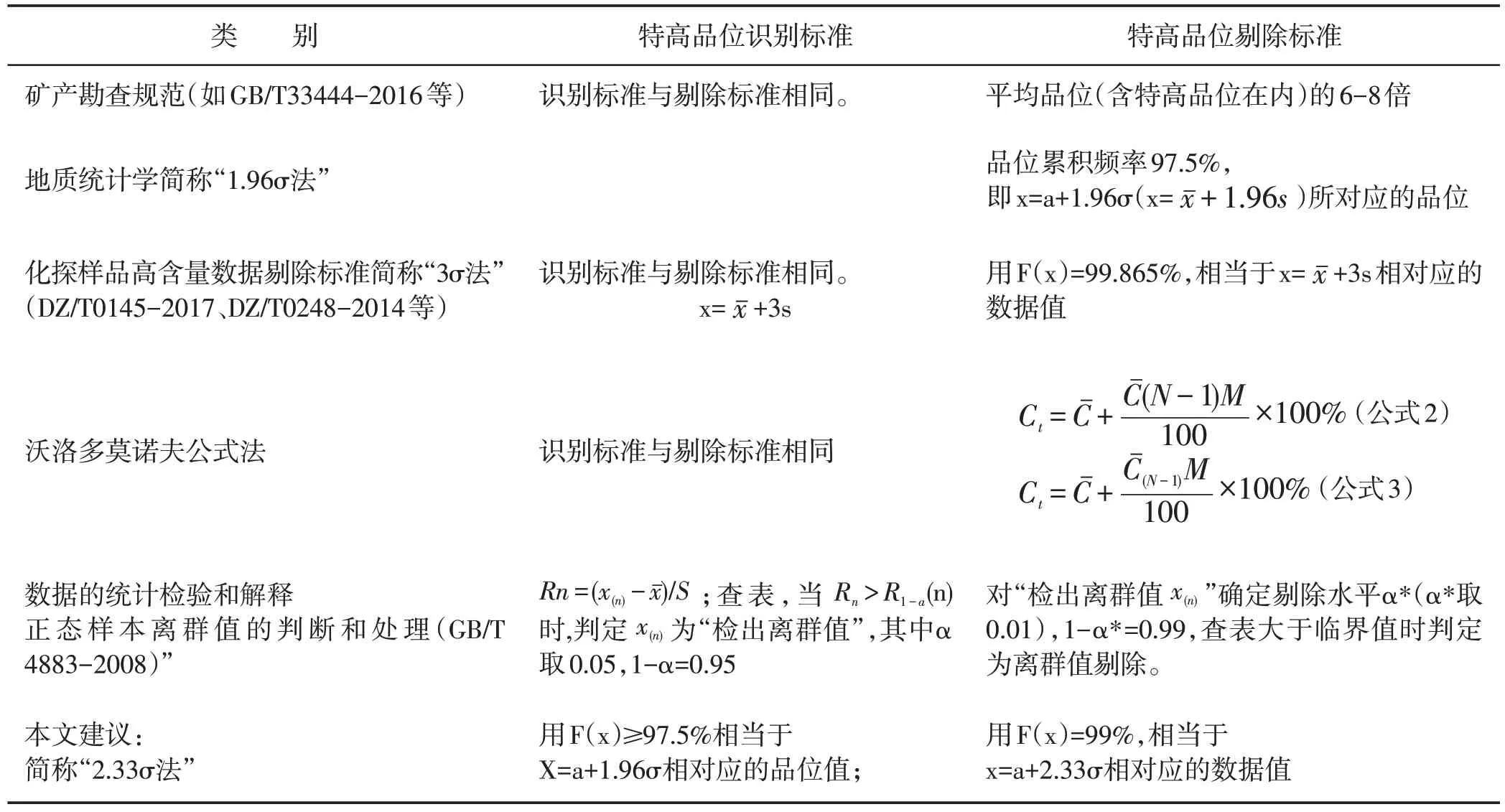
表2 特高品位下限标准Table 2.Lower limit standard of erratic high grade
4 特高品位识别、剔除标准的建议
笔者建议:一般情况下,从本矿床的矿石品位变化实际出发,运用GB/T4883-2008识别标准和剔除标准的理念,修正、补充地质统计学品位累积频率97.5%剔除标准的内容,用下述标准来识别、剔除特高品位:
识别标准:品位累积频率“F(x)≥97.5%”或“X=a+1.96σ”相对应的品位值;
剔除标准:品位累积频率“F(x)≥99%”或“X=a+2.33σ”相对应的品位值。
这样做,满足了如下要求:特高品位的识别、剔除,紧密结合勘查矿床品位分布的实际,避免了因用平均值6~8倍一刀切,造成脱离矿床品位变化的实际而产生的缺陷;补充、修正了地质统计学品位累积频率97.5%法则,提高了对特高品位识别、剔除的精度;满足了GB/T4883-2008 关于区分离群值的识别标准和剔除水平要求。
5 特高品位的处理方法
在实际工作中,特高品位是客观存在,由于主观因素对特高品位处理不当,在矿床开采过程中会造成很大困难。如果在富矿的分布范围,位置、品位、产状、变化规律等在开采前均未掌握,对合理安排生产会有很大影响。因此,特高品位的引起原因,要认真检查和研究。对特高品位的识别和剔除,要慎之又慎,须从本矿区品位变化的实际出发。
处理特高品位的方法是:首先要安排特高品位样品副样二次内检重分析,若分析无错误,再到取样地点进行检查。如果因取样原因造成错误,则该样品要作废重新补取,重新分析。通过上述方法,证明确系特高品位,按下述方法处理特高品位:
(1)确认特高品位存在:通过确定特高品位下限确认高品位值系特高品位;
(2)当重分析结果误差在允许误差范围内确定为特高品位时,用第一次结果作为待处理的特高品位。
(3)特高品位的剔除,不能多个样品一次性剔除。要逐个样进行,即剔除一个特高品位后,要对剩余的n-1 个样重新计算平均值、标准差和剔除水平,寻找第二个特高品位样剔除,……,顺序进行,第三个、第四个待剔除的特高品位,一步一步的计算、剔除,直到没有能剔除的样为止。
(4)用平均品位替代特高品位参加资源/储量平均品位计算,目前的做法是:用整个矿体、或整个块段、或特高品位工程影响范围的数个工程范围内的平均品位来替代特高品位样品的品位,重新计算得出单工程或块段平均品位。这个品位可以包括、也可以不包括特高品位;用本工程(坑道、钻孔)的平均品位替代特高品位;以特高品位下限值替代特高品位样品的品位,参加平均品位的计算。在工程素描图中,仍按分析结果进行计算、表示其实际平均品位。在采样平面图、中段地质平面图、勘探线剖面图、资源/储量估算垂直纵投影图中,工程平均品位、块段平均品位则按处理后的结果表示。
(5)若特高品位样品呈有规律分布,如某块段各工程相应地段均出现特高品位样,且可圈出高品位样带时,则单独圈定富矿带并计算资源/储量,这些样品不作为特高品位样品处理。
6 示例
某金矿区共取样151 个,一般品位为0.8~1.5g/t,少量为3~5g/t,其中有一个样为50.10g/t 高品位,经复检证实确系高品位。请进行特高品位的识别和剔除处理。
经计算,其算术平均品位、均方差及变化系数为:
=1.92g/t(包含一个高品位)s=6.20g/tv=321%
=1.21g/t(不包含一个高品位)s1=0.79g/tv=65%

如果用(5)式计算,则:
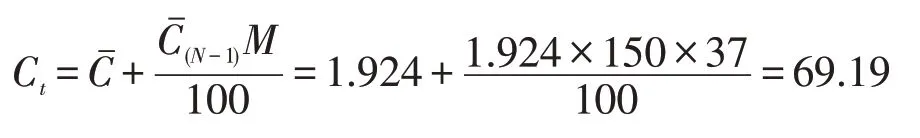
计算的结果:用(1)式计算的特高品位下限是108.7g/t,为平均品位1.92g/t的56.6倍,相当于f(c)=a+17.22σ所对应的品位值,出现的概率大约在百万分之一以下,对于金矿,从经验判断,所定的特高品位下限值过高,其结论不合理;用(5)式计算特高品位下限值是69.19g/t,为平均值1.92g/t的36倍,特高品位下限值相当于f(c)=a+10.85σ对应的品位值,出现的概率大约在十万分之一以下,下限值数据显然偏高。
如果用规范规定的方法,定位特高品位下限值是算术平均值8 倍:1.92g/t×8=15.37g/t;则其结论可以接受。
如果用累积曲线97.5%(1.96σ)法,特高品位下限值为:1.92+1.96×6.20=14.08g/t,为平均品位1.92g/t 的7.32倍,则其结论可以接受。
如果用累积曲线99%法(2.33σ)法则,特高品位下限值为:1.92+2.33×6.20=16.37g/t。它紧密结合本矿区品位数据分布(集中、离散)特征,剔除指标符合GB/T4883-2008离群值剔除规则,且为平均品位1.92g/t的8.52倍,其结论相对满意。
本案用各种方法计算的特高品位下限结果对比,如表3。
上述观点和建议,是笔者工作中的体会,系一家之说,抛砖引玉,片面和不妥之处,热忱期望读者批评指教。
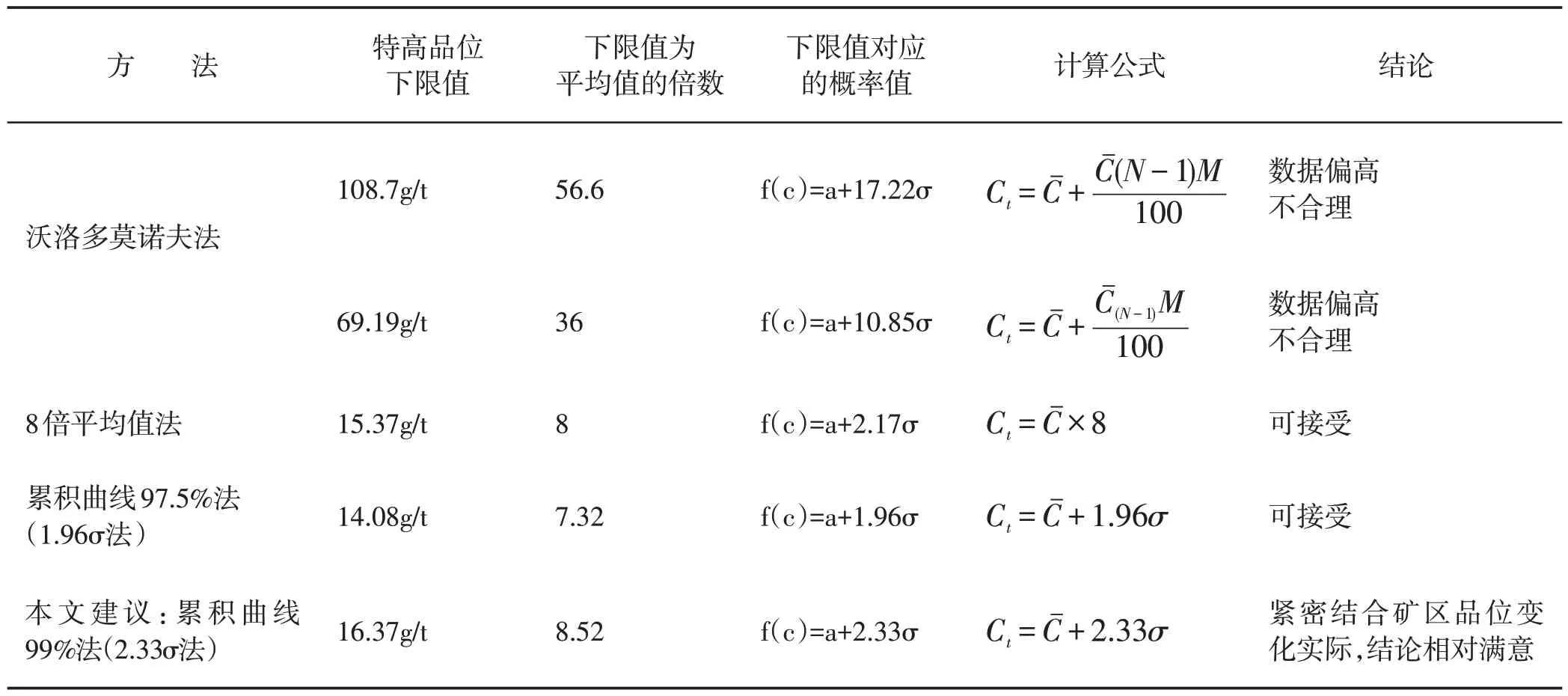
表3 某金矿区不同方法计算特高品位下限对比表Table 3.Comparison of lower limits of erratic high grades calculated by different methods for a gold field
