融合遗传算法和关联规则的数据挖掘方法改进

孙 红 李存进

（1.上海理工大学光电信息与计算机工程学院，上海，200093；2.上海现代光学系统重点实验室，上海，200093）

引 言

数据挖掘技术通过对数据对象进行定性处理，从而分析并得出一些潜在的有用的信息。利用数据挖掘分析方法对交通数据进行实时可靠的分析能够有效缓解交通压力改善交通服务[1]。遗传算法(Genetic algorithm,GA)作为一种基于自然选择和基于遗传学原理的随机并行搜索算法，在很多领域中都有成功的应用[2]，然而传统GA[3]存在早熟与搜索效率低的缺陷。自适应GA可以通过对其中2个重要参数，即交叉算子与变异算子，进行适当的自适应调整以达到全局最优与收敛速度之间的最佳平衡[4]。基于模糊GA的挖掘通过关联规则和模糊GA的合理融合有着更好的挖掘性能[5]，但依旧存在收敛性较差问题；有学者提出了基于聚类和基于专家经验相结合的自动筛选方法，实现了关联规则的数据挖掘在交通数据中的实际应用[6]；数据挖掘结合贝叶斯算法在气象数据中的应用也具有良好的预测效果[7]；模糊集和模糊关联规则的自动挖掘中，基于GA的自动聚类方法有显著的成效[8]。作为影响GA的2个重要参数：交叉和变异概率，很多学者对其加以改进以提高可用性与适用性，加快收敛速度，有学者通过非线性排序减少近亲遗传取得了不错的效果[9]，改进后的自适应GA算法的收敛性还可以通过采取最优保存策略得以保障[10]，而其交叉与变异算子也有着各种各样的改进以保障其全局最优的优势[11-12]。

本文提出一种将自适应GA和关联规则相融合的方法，对传统算法Apriori和FP-Growth[13]的优劣进行分析，最终选择GA用于交通数据关联规则的挖掘[14]，并根据其具体需求对GA进行适当的自适应改进。与此同时，通过引入亲密度的参数来适当调整其客观性。以Hadoop集群的搭建，将关联规则部署到大数据分析技术的流行开源平台——Hadoop上以提升挖掘海量数据的效率。

1 关联规则和遗传算法

Apriori算法[15]作为最经典的算法，其基础是频繁项集先验知识。Apriori算法的主要问题在于:为了搜索全部频繁模式，就要对事务库进行重复扫描，而且为了获得较长频繁模式，其过程中有着大量的候选短频繁模式产生，所以这就导致Apriori有着较大的时间以及空间复杂度。FP-Growth算法是Han在2000年提出的一个新的算法模型，用于解决这一瓶颈问题。算法主要分为2个过程：构造FP-Tree和挖掘频繁模式。研究表明，FP-Growth适应挖掘不同长度的频繁模式，其在效率上要比Apriori快出一个数量级[16]。当FP-growth搜索频繁项集时，它生成大量条件模式库并构造条件频繁模式树，这不仅影响频繁项集的挖掘效率，增加了数据库服务器的负担，对于海量数据而言，它的时间和空间复杂度依旧很大。

GA作为一种模拟自然进化过程搜索最优解的方法，因其在算法过程中无需产生大量的频繁模式，是Apriori和FP-Growth的有效补充。GA通过将实际研究对象的值按某种方式进行编码后转化为染色体，编码不仅简单易于实现，而且便于遗传算子的操作，这里选择实数编码方式，如表1所示。

表1 事务数据库Tab.1 Transaction database

事务数据库中的个体编码就是一个元素个数为n的实数数列，A[i]为字段i，i=1,2,3,…,n；用数值0～M[r]表示字段A[i]属性值，比如天气状况，可用“1”表示“晴天”，“2”表示“小雪”，这里，“天气”就是字段，而“晴天”和“小雪”就是“天气”这个字段的其中2个属性值。此外，“0”值被用来表示此属性与其他属性无关联。

染色体结构编码结构如表2所示。支持度和置信度在关联规则中有着很重要的作用，两者一高一低或者一低一高都说明规则是无效的。适应度函数在GA中用于评估群体中的每个个体的利与弊，起着关键性的作用，这里采用结合支持度作为适应度函数如下

表2 事务数据库中个体编码方式Tab.2 The individual encoding of transaction database

式中：X，Y分别为关联规则的先导(Antecedent/left-hand-side,LHS)和 后 继 (Consequent/right-hand-side,RHS)，min_sup为最小支持度阈值，Count(X⇒Y)为绝对支持度，关联规则X⇒Y相对支持度为sup(X⇒Y)=Count(X⇒Y)/|D|。X⇒Y为所需规则时，fitness(X⇒Y)＞1，而fitness(X⇒Y)＜1的规则于下一代的遗传操作中淘汰。故只有高支持度的个体才可以存活下来。

因为数据中记录量不同，字段数不同，字段属性不同，所对应的min_sup也是应该不同的，1000条20字段属性范围[1,10]的min_sup应该比100条10字段属性范围[1,3]的min_sup要大，所以min_sup必须和实际情况相符合，这里取min_conf=40%，而min_sup的动态变化如下

选择是一个选择较优个体的操作。由于传统的选择算子没有考虑到关联规则的支持度和置信度，因此，本文选择将相对支持度大于min_sup的个体都将被保留进入到下一代。交叉操作作为GA的关键步骤是将2个父代个体的染色体进行部分基因的交换从而得出新的子代个体，本文选用单点交叉方式。本文采取的染色体编码方式是实数编码，结合单点交叉，再在此基础上融入均匀交叉的思想，设定好交叉点后，任意选择进行互换的部分无论是交叉点前面的还是后面的基因，都能避免无关基因过早收敛。变异在GA中能够维持群体的多样性[17]。

2 改进GA和关联规则的数据挖掘方法

对于GA而言，有一个不可避免的问题就是容易早熟问题，而交叉概率Pc和变异概率Pm可以对这一问题有一定的避免作用。对于传统GA而言，Pc和Pm都是常数，一般取值为Pc∊ [0.4,0.9]，Pm∊ [0.01,0.1]。在 GA 进化的早期阶段，如果使用固定的Pm值，当Pm较小时不会对群体产生什么影响，利于新基因的产生，较大会破坏群体的优秀基因。也就是说虽然交叉概率越大，算法的搜索区域越大，但是却会导致遗传模式很容易被破坏，过小又会使得搜索时间过长，过程缓慢，算法显得很迟钝。对于变异概率而言，过大会使其成为一般性的随机搜索算法，反之难以产生新个体[18]。自适应GA对这2个参数进行动态变化，这种动态变化是根据其进化的代数以及适应度进行的合理调整。适当对Pc和Pm变化使得产生出的个体能够作为相对优良个体从而保护其优良性。反之，比平均值小则需增大Pc，减小Pm。在这种调节方法下的GA无需过大的进化代数就更容易减弱全局搜索能力，慢慢增加其局部搜索能力，提高算法效率与适用性。

在解决实际问题时，一般希望算法可以在一开始快速搜索，当获取的遗传模式越来越好时，放慢脚步，保护遗传模式。因此，文献[11]对交叉、变异概率进行了自适应改进，有

文献[12]对文献[11]的Pc和Pm进一步改进如下

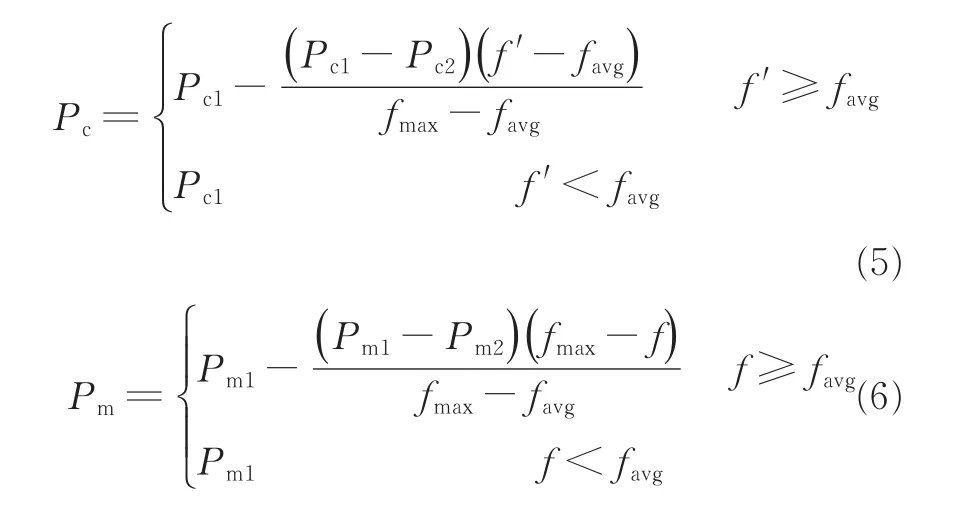
式中：fmax为整个的最大适应度值，favg为每代的平均值，f'为2个要交叉的个体中较大值，f为要变异个体的值，Pc1和Pc2均为交叉概率，取值Pc1=0.9，Pc2=0.6，Pm1和Pm2均为变异概率，取值Pm1=0.1，Pm2=0.01。该自适应改进在求解类似旅行商（Traveling salesman problem，TSP）等问题时有不错表现，但是应用在关联规则当中，当f'≥favg时Pc值只在(Pc1-Pc2)的小范围内变动，其主要原因是个体支持度与最小支持度的比值波动范围不是很大，所以导致没有明显的自适应效果。

本文对Pc和Pm值进行如下改进

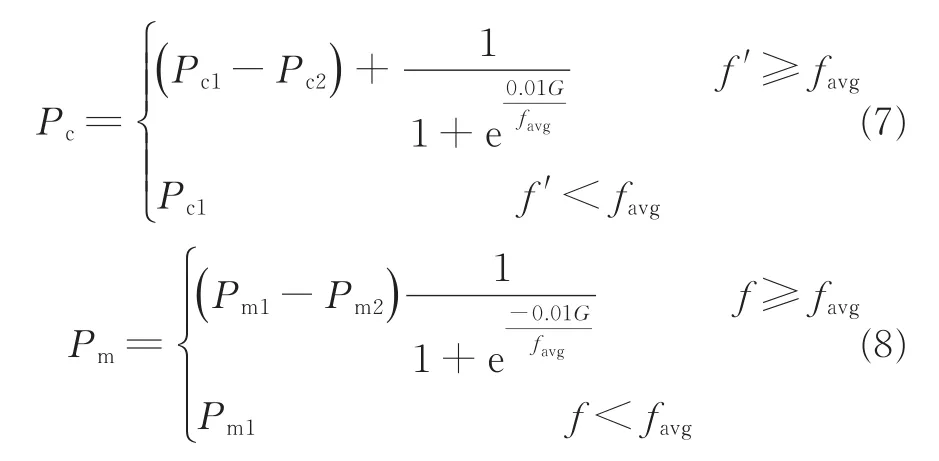
式中:Pc1取值为 0.9，Pc2取值为 0.6，Pm1取值为0.1，Pm2取值为0.01，终止条件为最大进化代数MaxGen=1000。

为解决一般关联规则中出现的不相关的无用规则问题，本文引入了一种新的方法——亲密度，以避免实际问题中出现的负相关关系，从而规避无用规则，提高实用性和可靠性。亲密度的定义如下

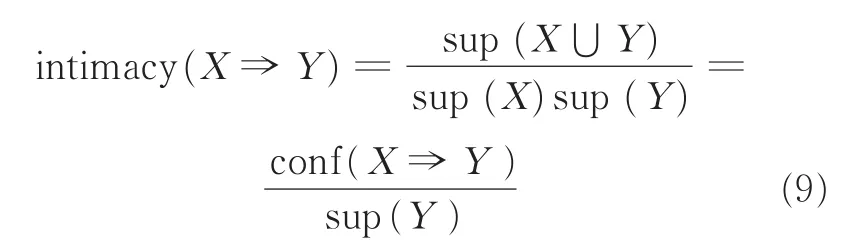
式中：置信度为conf(X⇒Y)=Count(X⇒Y)/Count(X)，最小置信度表示为min_conf。当intimacy(X⇒Y)=1时，称为不相关规则，即两者是相互独立的；intimacy(X⇒Y)＜1称为负相关，即项目集合Y会因项目集合X的发生而减小其发生的可能性；intimacy(X⇒Y)＞1称为正相关，即Y会因X而增加发生的可能性。

基于式（9）亲密度的挖掘模型如图1所示。

图1 引入亲密度的关联规则模型Fig.1 Association rule model framework with intimacy

算法流程如下。

步骤1初始化Pc,Pm,n等参数，随机生成初始种群Porigin={A1,A2,A3,…,An}。

步骤2计算min_sup和种群Porigin中每个个体的适应度fitness(X⇒Y)。

步骤3个体是通过基于适应度比例选择从群体中选出，如果fitness(X⇒Y)≥min_sup则复制到下一代个体，否则保留并计算m。

步骤4如果m＜n，随机生成n-m个个体，并根据式（7，8）进行自适应遗传操作和变异操作。

步骤5对规则集中的个体进行判断，分别计算每个规则(X⇒Y)的sup(X⇒Y)，conf(X⇒Y)和 intimacy(X⇒Y)。

步骤6如果满足sup(X⇒Y)＞ min_sup， conf(X⇒Y)＞min_conf和intimacy(X⇒Y)＞1的条件，那么取Best_Rules=Best_Rules U{(X⇒Y)}。

步骤7获取相关性并提取强关联规则。

3 实验结果及分析

3.1 实验数据与环境

本实验先后采用了气象数据集和某城市交通事故数据集进行改进算法的验证，因气象数据集涉及卫星云图的安全问题，不能获取即时的准确信息，存在一定误差，所以本文主要以交通事故数据集进行了实验分析。该交通事故数据集包含了丰富的信息，有45个字段，包括发生事故时候道路的等级、位置特征、当时的天气情况等，特定事故数据情况的字段，每个要素及其编码值如表3、4所示。

表3 字段编码值对应数据表Tab.3 Field encoding value data table

表4 编码与各要素对应表Tab.4 The corresponding table of codes and element

“云计算”技术即为通过网络访问非本地资源的计算服务（包括数据处理、存储和信息服务等），这些资源能够方便且高效地部署，并不用过多的人为操作[19]。Hadoop是Apache Foundation开发的开源分布式计算平台，Hadoop MapReduce是在硬件集群上并行处理大量数据的软件框架。MapReduce将大型作业划分为较小的作业，然后并行处理这些作业，最后将其结果存储在分布式文件系统中。MapReduce将数据的处理分为Map和Reduce这2个主要阶段进行[20]。Map阶段的任务执行过程为：Map:Reduce的执行过程为pReduce流程图如图2所示。Hadoop的框架最核心的基础架构就是其分布式文件系统（Hadoop distributed file system,HDFS）和并行计算框架MapReduce（Google MapReduce的开源实现）。HDFS为大量数据提供存储，而MapReduce为其提供计算[21]。HDFS架构如图3所示，HDFS的主控节点为NameNode，HDFS从节点为DataNode，用于存储大规模数据。MapReduce的主控节点为JobTracker，MapReduce的从节点为TaskTracker，用于管理每个节点上计算任务的执行。数据存储主节点NameNode和并行计算主节点JobTracker可以设置在同一主节点上或2个不同节点上[22]。

图2 MapReduce处理过程流程图Fig.2 MapReduce process flow chart

由于需要处理大量数据，本文使用具有完全分发模式的Hadoop平台。实验搭建4节点集群，其中1个节点作为Namenode和JobTracker的服务节点，其他3个节点作为Datanode和Task-Tracker节点。节点IP分配以及每个节点的功能如图4所示。

图3 HDFS架构Fig.3 HDFS architecture

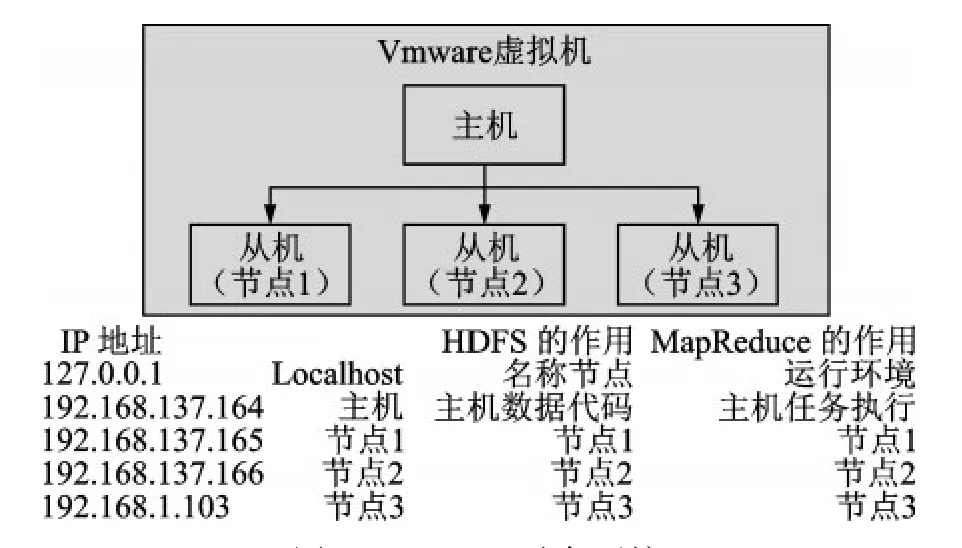
图4 Hadoop平台环境Fig.4 Hadoop platform environment

首先在一台计算机上随机产生n个群体，然后用MapReduce将群体分而治之，将群体分为m个部分，对每一部分单独进行计算与遗传操作。流程图如图5所示。

图5 融合GA算法的关联规则挖掘MapReduce化Fig.5 Association rule mining based on GA and MapReduce

3.2 改进自适应GA算法结果分析

交叉概率Pc和变异概率Pm的曲线如图6,7所示。由图6可知，Pc随着进化代数的增加而减小，最后趋于0.3。由图7可知，Pm随着进化代数的增加而增大，且最后趋于0.09。改进后的算法在进化刚开始阶段新个体的生成主要受到交叉算子的影响，但是随后由于交叉概率趋于一定值，从而使优良基因得以保护。同样地，初期变大的Pm又可以帮助其脱离局部最优从而产生新个体。

图6 改进自适应Pc线图Fig.6 Improved adaptivePccurve

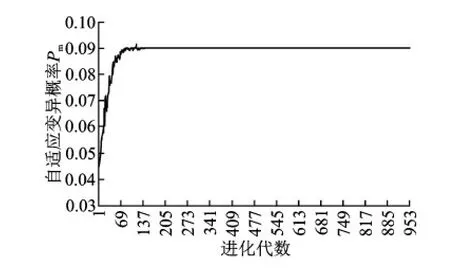
图7 改进自适应Pm曲线图Fig.7 Improved adaptivePmcurve

3.3 不同优化的遗传算法对比实验及结果分析

将经典GA、文献[12]算法（改进1）和本文的改进算法（改进2）应用于关联规则挖掘后的实验结果如图8所示。

由图8可知，本文改进算法在解的质量方面与经典算法和改进1算法相比均有一定的提升。

图8 改进自适应GA算法与经典GA算法对比Fig.8 Comparison between improved adaptive GA and traditional GA

3.4 FP-Growth算法效率和自适应遗传算法效率在交通数据的实验对比分析

算法效率由于会受到数据中的要素个数、属性的取值范围以及数据量的影响，据此将FP-Growth算法效率和改进后的融合GA与关联规则的算法效率在这三方面进行比较，得出时间比（优化自适应GA/FP-Growth）的曲线图如图9,10,11所示。

从结果可得GA挖掘多字段多属性值时优势显著，虽然随数据量递增，GA的计算效率较FP-Growth算法较低，但其加速比在可接受范围之内，如果字段数，也就是数据库中交通事故的属性越多，则改进GA的效率相比较FP-Growth越好；同样，若每个属性的取值范围越大，改进GA的效率也更好；但是，改进GA对于递增的数据库数据量没有FP-Growth表现好。综上，改进自适应GA较FP-Growth算法更适用于结构复杂的交通事故数据挖掘，虽然GA比FP-Growth对于数据量递增时效率较低，但二者差距不大，当数据量在10000条记录以下时比值都在4以下，而当数据量超过10000条时，二者算法效率都比较低，所以进一步并行化可解决算法对大数据的处理。综合来看自适应GA更适合挖掘结构复杂的交通数据。

图9 交通数据要素个数下的时间比(数据量：1000，属性取值范围：[1，10])Fig.9 The time ratio under the number of traffic data elements

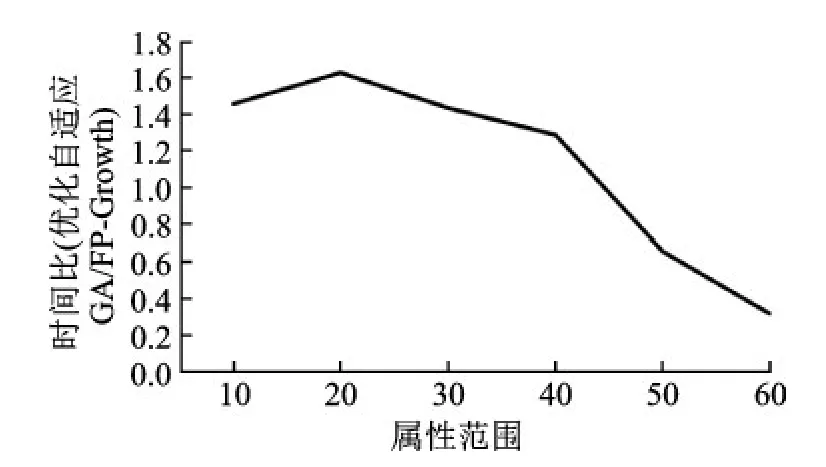
图10 属性范围下的时间比(属性范围(数据量：1000，字段数：20))Fig.10 Time ratio under property range

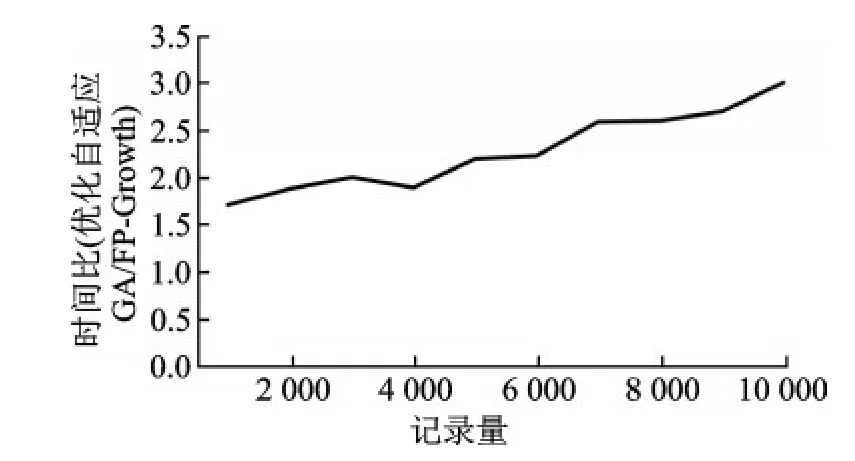
图11 记录量下的时间比（交通要素个数：20，属性值取值范围：[1，10]）Fig.11 Record the time ratio under the quantity

当挖掘好频繁模式后，对频繁模式进行置信度计算，挖掘强关联规则，提取后的结果以1000条记录、20个字段、属性取值范围[1,10]为例有：

(1)酒后驾驶和疲劳驾驶引发的交通事故较多（支持度很高）；

(2)发生事故地点附近写字楼密集，即交通流量大，则人员死亡数相对较低；

(3)恶劣天气，包括雪天、雾天在快速路上发生交通事故较多；

(4)违反交通规则的驾驶员容易造成交通事故。

4 结束语

本文针对交通数据未被充分利用、潜在价值未被充分挖掘的问题，提出了关联规则在智能交通中的应用，利用自适应GA的全局优化能力将其融合到关联规则中，最后在提取规则前引入了亲密度的度量方法提高了可靠性。通过Hadoop平台进行实验验证，实验表明改进后的方法在算法的收敛性以及解的质量上均有一定优势，且挖掘效率较传统方法有一定的提升，也进一步证明了大数据分析技术在智能交通挖掘上的优势。然而对于更为复杂的实际数据所生成的复杂离散属性，可能会显得有所不足，接下来的研究工作可通过引入神经网络对数据中的特征进行细化分析以提高方法的精度。