多镜头组合式相机的全景SLAM

季顺平，秦梓杰

武汉大学遥感信息工程学院，湖北 武汉 430079

随着传感器、自动化和平台技术的发展，利用平台上安置的光学或距离传感器，同时实现自我定位与环境感知的智能系统成为摄影测量、计算机视觉和机器人学的新型研究方向[1]；并在移动测图系统、无人驾驶汽车、火星和月球的深空探测、无人机侦察、室内导航等领域发挥着关键的作用[2-3]。若以光学传感器为主要信息获取源，这种系统通常称为基于视觉的自动定位与地图构建(simultaneous localization and mapping,SLAM)[4]。主流的视觉SLAM系统有两种分类模式。一类按照所采用的传感器划分。包括单目SLAM(mono-SLAM)、双目SLAM(stereo-SLAM)和4D相机SLAM(RGBD-SLAM)。另一类按照所采用的方法划分，主流是基于点特征的SLAM(feature-based SLAM)和基于图像自身的SLAM(direct SLAM)。成熟的、具代表性的SLAM系统如：基于特征点的ORB-SLAM[5]，直接法的LSD-SLAM[6]，将特征点法与直接法混用的SVO[7]、SVO2.0[8]，以及RBG-D SLAM的代表作RTAB-MAP[9]，等。

这些主流SLAM架构采用传统框幅式的相机或摄像机作为视觉信息获取装备。单目SLAM视场狭窄，尺度估计受累积误差的影响，较依赖于闭环条件[10]。双目SLAM虽然克服了尺度漂移，但是视差狭窄依然没有改变。若局部成像区域信息较少(即提取的ORB[11]或其他特征较少)，或者出现较大的视角变化，则会引起跟踪频繁丢失。这也是SLAM技术尚未广泛应用于测绘行业的地面移动测图系统(mobile mapping system,MMS)的关键因素。

大视场成像设备，如鱼眼镜头和全景镜头，理论上能够克服视场狭窄的问题。全景视觉成像具有360°全视角成像的优势，已经在测绘、机器人、计算机视觉等相关领域中逐步得到应用[12-13]，如用于城市测图、视频监控、交通监督、虚拟现实、机器人导航、场景重建等。装载于移动测图系统或普通汽车上的全景成像装置通常只被用于街景收集，如谷歌和百度的街景图像，无法实现量测功能；基于全景视觉的检校，几何定位或完整的SLAM系统也有较多的研究[12-22]。文献[18—19]采用超广角单目鱼眼相机，使用卡尔曼滤波作为优化方法；文献[17]与SVO2.0[8]研究了多镜头组合系统的SLAM算法，前者采用了球面模型的粒子滤波作为优化方法，而SVO2.0采用了多个平面相机模型，以光束法平差进行优化；文献[16]使用直接法光流跟踪作为前端的视觉里程计，光束法平差作为后端优化方法；因此也继承了直接法的优点与缺点。本文尝试将多镜头组合式全景相机与基于特征的SLAM方法(ORB-SLAM2[23])相结合，发展一套基于特征的三线程单目全景SLAM系统。

生产完美的球形镜头受到当前制造工艺的限制。移动全景视觉成像主要采用3种替代模式：多镜头组合式、旋转式、折反射式[19]。其中，多镜头组合式是目前最流行的移动全景成像技术，它借助一系列的鱼眼相机分别成像，再拼接为无缝全景图像。目前已经实现了商业化生产，如PointGrey公司的Ladybug系列，中国测绘科学研究院也有相关产品。旋转式成像借助一根CCD的高速旋转，实现360°的连续成像。文献[14]曾研究过旋转式全景相机的传感器成像模型和自检校方法。然而，只有2000年前后德国的Noblex公司生产过少量的相关产品。折反射全景相机包括两个组分：镜子和透镜。镜子首先折射周围的光至透镜，透镜再实现成像。由于复杂的成像机理和制造工艺，折反射全景相机应用相对较少，也没有商业上的推广[24]。本文的全景SLAM以多镜头组合式全景相机作为视觉信息的获取装备。

目前，视觉SLAM已经得到了蓬勃的发展，基于单目、双目和RGB-D相机的SLAM技术日臻成熟，能应用于全景相机的SLAM系统也有较多的研究。多镜头组合式全景相机的原理已经由[25—27]等文献建立，鉴于全景视觉的独特优势，发展一套高度自动化的、基于特征的多镜头组合式全景相机的SLAM系统并实现高精度的量测功能，无论在测绘行业还是机器人与计算机视觉都具有积极的意义。本文从全景构像方程、鱼眼相机检校、初始化、局部地图构建、关键帧选择、全图优化等各个步骤探讨基于全景相机的完整的SLAM方法，并在每个步骤中都做出了大量创新性的工作。

1 全景相机的成像、检校与优化模型

1.1 多镜头组合式全景相机模型

多镜头组合式全景相机由一系列独立、固定的鱼眼镜头组成，多个镜头独立成像，再拼接为全景图。如图1(b)所示，每个镜头具有各自的投影中心C，在实际制造过程中尚难以保证与球心S完全重合。可见，物理上的三点共线是C、uc和P′。这是独立镜头的成像方程。为了实现统一的全景坐标系统，需要将实际像素坐标uc投影到某个指定半径的球面上，得到u。此时，所有的鱼眼图像坐标就可投影至统一的球面坐标。

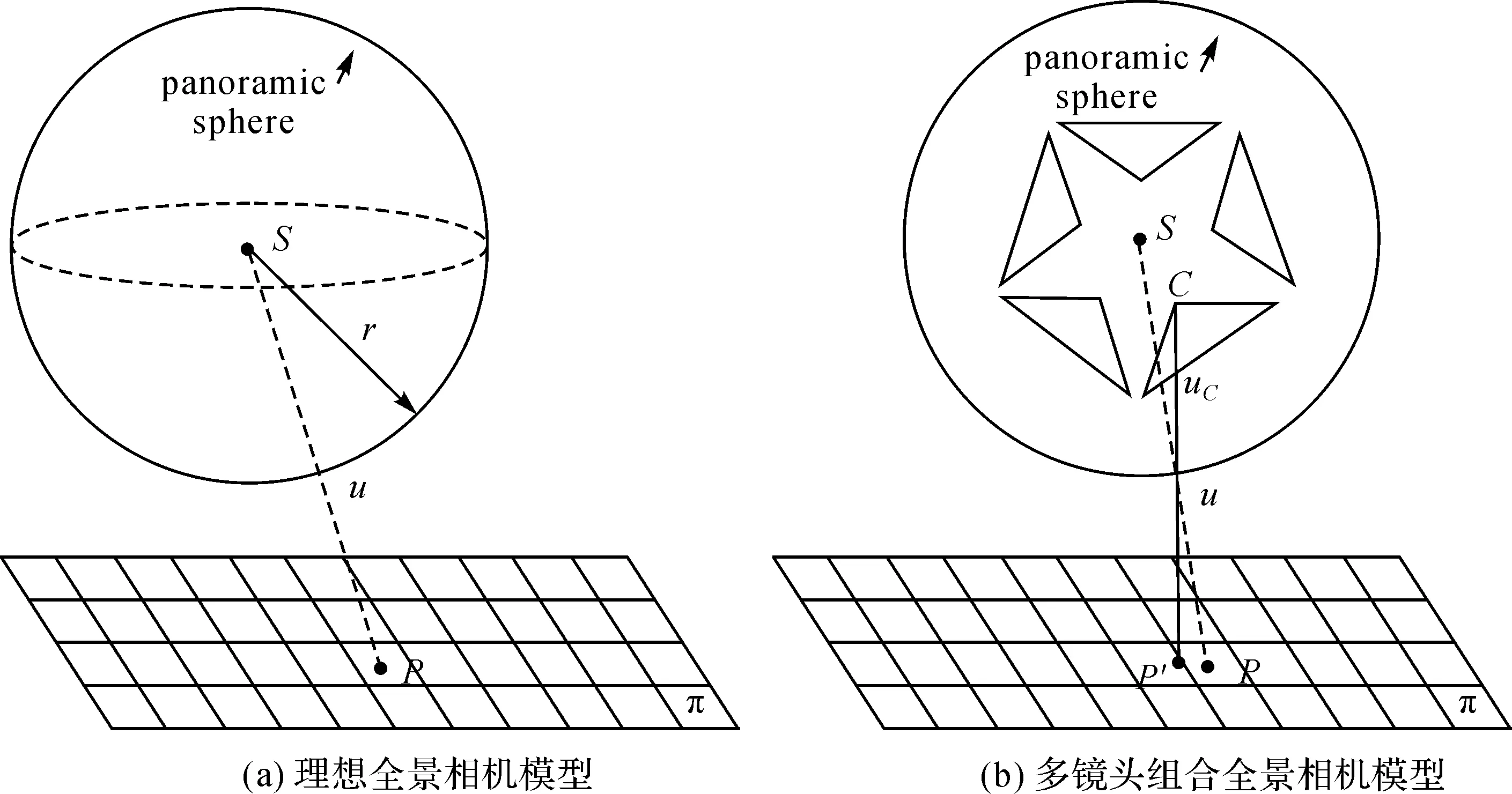
图1 全景成像模型Fig.1 Panoramic imaging model

因此，第1步需要将独立相机的图像坐标转换为统一的全景球面坐标。描述单相机像点uc(其坐标用x表示)计算全景球面像点u(其坐标用x′表示)的过程如式(1)所示

x′=mRiKi(x)+Ti

(1)

x′2+y′2+z′2=r2

(2)

式中，Ki是第i个鱼眼镜头的内参函数，参量包含镜头畸变差、CCD畸变差、焦距、主点等；Ri和Ti分别表示第i个鱼眼镜头投影中心在全景坐标系中的旋转矩阵和偏移矢量；Ki、Ri、Ti通过严格标定之后即为固定值；m为球面半径r所确定的比例系数，联合如式(2)所示的球面方程可同时解得m和x′。

从图1可见，用于表述共线条件方程的光束是CuP′而非SuP。首先表达真实的射线(x′-Ti)，并将其平移至统一的球面坐标(加上平移量Ti)，得到共线条件方程

Ti+λ(x′-Ti)=[R|T]Xw

(3)

当Ti取值为0时，式(3)就表达一个完美的球面成像模型(图1(a))，许多文献都采用近似的理想成像模型[15，22]。本文将成像模型用于SLAM系统，需要像点、世界点之间的精确的正反算，因此保留参数Ti。

1.2 鱼眼相机的检校

内参函数Ki可采用不同的相机检校模型。鱼眼镜头的内参数同样需要精确的检校才能保证在一系列坐标转换中保持高精度。文献[28]提出了一种通用鱼眼相机检校方法并得到广泛的应用。如式(4)所示

Xd=(k1θ+k2θ3)ur(φ)+Δr(θ,φ)ur(φ)+

Δt(θ,φ)μφ(φ)

(4)

式中

Δr(θ,φ)=(l1θ+l2θ3+l3θ5)(i1cosφ+i2sinφ+

i3cos 2φ+i4sin 2φ)

Δt(θ,φ)=(m1θ+m2θ3+m3θ5)(j1cosφ+

j2sinφ+j3cos 2φ+j4sin 2φ)

Xd=(xdyd)T是鱼眼相机坐标；θ和φ分别是天顶角和水平角。lk、mk、ik、jk为多项式系数。试验表明，基于该方法检校鱼眼相机并生成核线立体像对，其核线误差约1～1.5像素。为使得核线误差降低到1像素以下，本文对改模型加以改进，提出一种更为精确的鱼眼相机检校方法。如式(5)所示

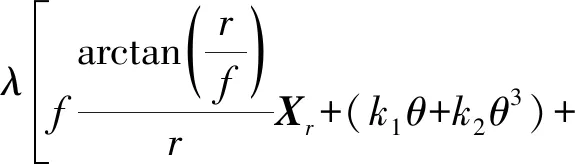
Δr(θ,φ)+Δt(θ,φ)+(A1r2+

(5)

式中，θ与φ可以由像素坐标计算得出。此模型共23个参数，因此需要12个或以上原始图像与纠正后图像的同名点坐标，以求解模型参数。本文显式地加入了鱼眼相机的成像过程(等式右边的第1项)，并将式(4)作为其系统误差的附加参数项。这样就减轻了通用多项式模型的拟合负担(即拟合微小的系统误差而不是将鱼眼投影模型都看作系统误差)。本文选取全图像均匀分布的72个点进行最小二乘求解，相机检校精度均在1个像素以内。

1.3 全景相机单像解析和前方交会

全景相机的定位全部在统一的全景球面坐标系下，即在原始鱼眼相机提取的特征点先根据式(3)转换到球面坐标系下。两个全景球上的同名特征点同样满足对极几何关系[18]，也即共面条件方程，如式(6)所示

(6)

从鱼眼相机坐标计算得到的球面坐标点已经包含了相机内参信息。直接解算式(6)可得到两个全景球之间的本质矩阵E。使用SVD分解获取旋转矩阵R与平移分量t，分解得到4个解。通过局部坐标系下球面特征点及其地图点在同一个方向作为判别依据，可选出正确的R与t。平移量t具有尺度不确定性，本文将当前场景的平均深度归一化从而确定t的尺度，并使用李代数SE(3)的形式表示相机位姿。

获取相机位姿的同时，需要根据匹配的特征点计算其地图点。球面坐标的前方交会公式如式(7)所示

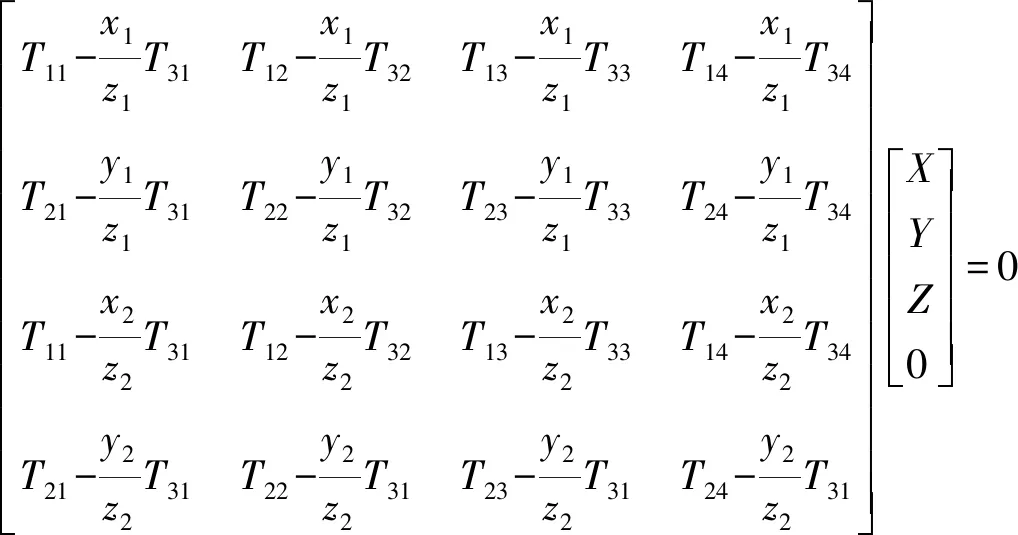
(7)

将同名点代入式(7)可解算得到地图点坐标。式(7)中，T=[R|t]为变换矩阵，x1与x2为同名球面特征点。

当已知相机位姿的初始值以及全景球面上的特征点所对应的地图点时，采用最小二乘法构建目标函数使球面重投影误差最小

(8)

式中，ξ∈SE(3)为当前位姿的李代数表示；Xw为地图点的世界坐标，两者为未知参数；Xs为特征点的球面坐标观测值；r为全景球半径。

获取有效初值是最小二乘法的关键步骤。若已知图像特征点与地图点的对应关系，文献[29]所提出Efficient Perspective-n-Point(EPnP)算法可用于解算位姿的初始值。EPnP在跟踪失败后的重定位过程发挥着重要的作用，本文提出并建立了球面模型上的EPnP方法，用以求解位姿初始值。根据球面投影关系

(9)

式中，t为比例因子；(xj,yj,zj)为控制点坐标；αj为坐标权重；(u,v,w)为球面点坐标。消元可得到球面坐标系下控制点坐标的齐次方程

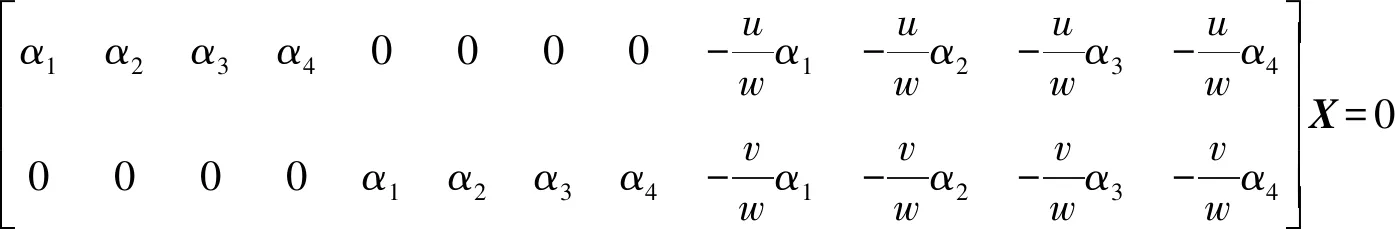
(10)

式中，向量X具有12维，设有n个地图点参与计算，则M矩阵具有3n维，M矩阵的核空间变为向量X的解。至此，4个控制点在全景球坐标系下的坐标及其在世界坐标系下的坐标已求出。再根据式(9)可得出所有正确的3D-2D匹配点在全景球坐标系及对应世界坐标系下的坐标。根据文献[29]所述的坐标对齐方法即可解除位姿估值[R|t]。

1.4 全景相机的非线性优化方法

本文的非线性优化方法基于g2o库[30]。而g2o中的所有优化方法只针对普通平面相机模型。本文对相关的优化算法进行改进，使其能够处理全景成像模型。借助于图论，待优化变量，即位姿、地图点设定为图的顶点，重投影误差(如式(8))设定为边，得到优化图(图2)。结合g2o并给出误差函数式(8)的解析导数形式，即误差函数对于位姿及地图点的雅克比矩阵，即可进行优化求解。假定球面位姿表达为ξ∈SE(3)，PC=exp(ξ^)，地图点为PW=(XYZ)T且L=X2+Y2+Z2，e是代价函数。则e对于位姿的雅克比矩阵为

(11)

式中

(12)

(13)

e对于地图点的雅克比矩阵为

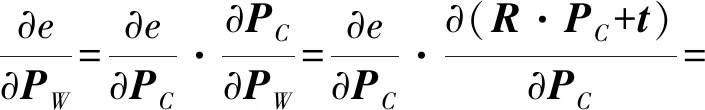
(14)

式中，[R|t]=exp(ξ^)。

本文实现的优化算法包含4类：单帧位姿优化(仅根据匹配的地图点计算当前帧精确的位姿，图2(a))、局部地图优化和平差(根据局部共视关键帧优化位姿与局部地图点，图2(b))、图优化(即essential graph优化，用于检测到闭环后，对全局关键帧的位姿进行调整，图2(c))、全局光束法平差(优化所有位姿和地图点，图2(d))。

鱼眼图像上不同位置投射到球面上的变形不同，例如，在本文试验中相机中心位置x0处一个像素的宽度，投影到球面上为0.037 6 m，图像边缘处一个像素宽度投射到球面上表现为0.014 45 m，因此，不同的点x采用不同的误差域值，阈值s设定为

(15)

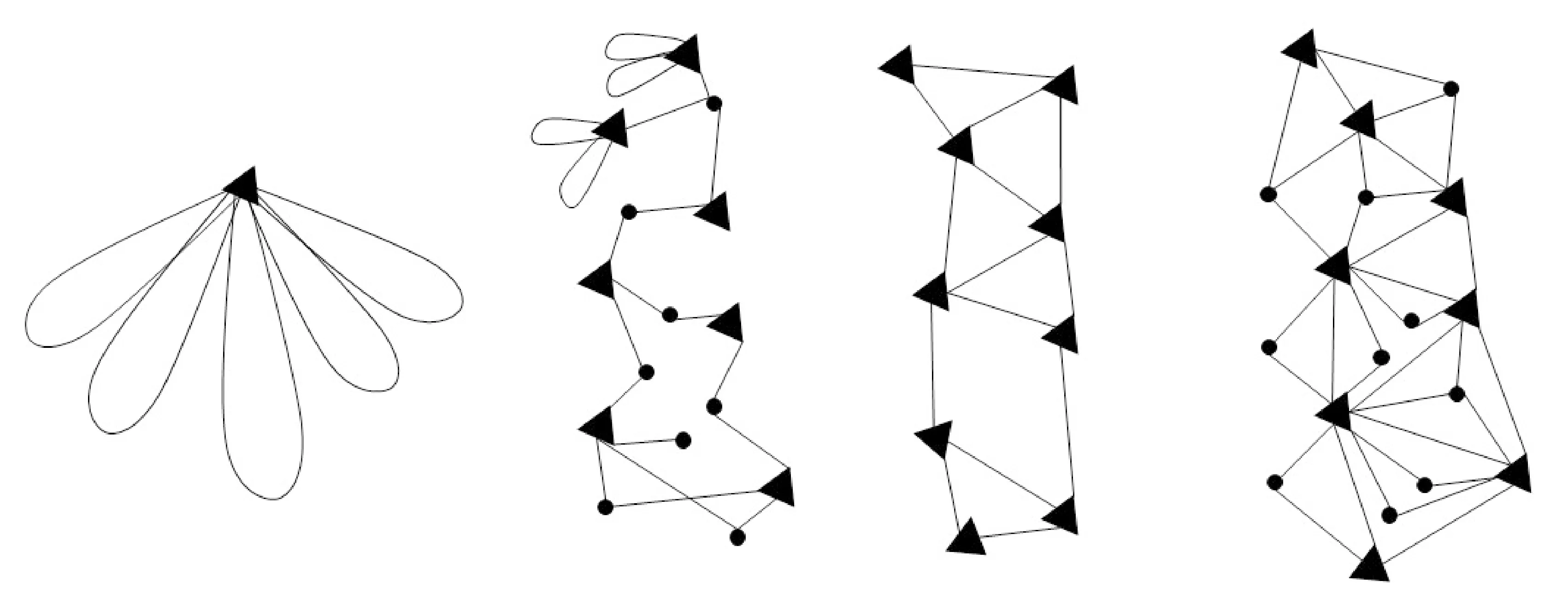
图2 构建的优化图(三角形节点代表位姿，圆形节点代表地图点，边代表误差项)Fig.2 Constructed optimization graph (in which the triangle node represents the pose, the circular node represents the map point, and the edge represents the error term)

2 全景SLAM流程

系统将分为3个线程并行工作，分别为跟踪(tracking)，局部地图构建(local mapping)与闭环(loop closing)。跟踪线程主要负责系统初始化，地图点跟踪，关键帧选取与位姿优化等功能，局部地图构建线程主要负责特征点三角化，误匹配点与冗余关键帧剔除，局部地图优化等功能，闭环线程主要负责闭环探测，闭环关键帧位姿改正与全局地图优化等功能。以下将逐一介绍各模块的算法策略。

2.1 初始化

本文将ORB(oriented FAST and rotated BRIEF)特征[11]用于SLAM系统的特征提取。本文针对全景相机做了系统初始化的优化工作。首先，鱼眼相机变形较大，匹配难度高，误匹配数量大。因此采用三帧而非两帧进行初始化。确定第1帧为参考帧，提取ORB特征点，等待系统连续传入两帧，进行第1帧与第2帧，第2帧与第3帧的特征匹配。然后结合RANSAC剔除误匹配点，保留3帧共视点，计算1-2帧和2-3帧的基础矩阵F。1-2、2-3、1-3组合分别进行三角化，得到3组3D地图点坐标值，设定3个地图点之间的空间距离阈值为0.08 m若有任意两个地图点坐标值的空间距离大于0.08 m，则认为此地图点不稳定，将其剔除。若成功三角化的点数量大于正确匹配点数量的75%，则调用优化模块进行平差并剔除误匹配点。若平差后正确匹配点数量大于30个则视为初始化成功，否则判定为失败，将第2帧作为参考帧，等待系统传入第4帧，使用2、3、4三帧进行初始化，依次迭代，直到初始化成功。

2.2 地图点跟踪

地图点的跟踪是SLAM自动化的关键环节。在算法1中，列出了全景相机地图跟踪的算法。

算法1 跟踪地图点

(1) 采用恒速模型实现3D地图点到当前2D图像的匹配定位。若成功，则结束，否则进入(2)。

(2) 采用2D图像到2D图像的立体匹配定位。若成功，则结束，否则进入(3)。

(3) 采用多视图像匹配，作为初值，再进行3D地图点到2D当前图像的匹配。若成功，则结束，否则进入(4)。

(4) 重定位。采用视觉词袋和PnP解法，实现匹配并定位。

(5) 只要(1)—(4)有一步成功，调用位姿优化模块进行位姿优化。

步骤1：采用恒速模型(速度和角度不变)跟踪下一帧地图点。首先，利用恒速模型估计当前相机位姿的初始值，将上一帧观察到的地图点投影到当前帧的全景球面上。然后，根据球面特征点坐标与鱼眼相机的外方位元素，判断该点所在的鱼眼相机编号。最后根据模型(3)反投影到鱼眼图像上设定搜索窗口进行特征匹配。同时计算地图点到全景球面的距离。本文假定当前恒速模型的水平旋转角度绝对值为θ，地图点到相机中心距离为d，则窗口大小W自适应地设为

(16)

确定搜索窗口后，在窗口内搜索同名特征点。这里的匹配阈值设置为：最邻近次临近之比大于0.7且描述子距离小于70。对所有地图点进行逐个匹配，若匹配数大于20则认为匹配成功并结束跟踪步骤。否则进入第2步。

步骤2：在步骤1，即3D地图点到2D图像的匹配失败时执行。采用图像到图像匹配策略，方法是视觉词袋(bag-of-words,BoW)技术。在当前帧与上一帧的特征点间进行匹配，若匹配点数小于10则进入第3步。若匹配点数在10～25之间，则扩大搜索范围，匹配从当前帧直到上一个关键帧所观察到的所有地图特征点。若匹配点数大于等于25，设上一帧的位姿为当前帧的位姿，执行位姿优化同时剔除误匹配粗差点(图2(a))，统计优化后的正确匹配点个数。若小于15，进入第3步；否则判定为匹配成功，返回位姿并结束。

步骤3：采用多视匹配获取当前帧位姿初值并用于匹配。使用当前帧与前两帧的所有特征点进行匹配，并提取三度重叠点。计算当前帧与前一帧的本质矩阵E，SVD分解后得到位姿初值，使用该初值将前一帧地图点投影到当前帧，并进行匹配。搜索窗口大小设置方式同式(16)。若匹配点数小于30则判定失败，进入第4步。若匹配点数大于30，则执行位姿优化模块。剔除粗差后若匹配点数再次小于30，则采用第2步BoW的匹配点执行位姿优化模块同时剔除误匹配点。若正确匹配点数大于15则判定成功，返回位姿；否则进入第4步。

步骤4：在以上匹配都失败时，进行重定位(re-localization)。使用BoW搜索上一帧到上一个关键帧的所有匹配点，调用PnP配合RANSAC进行重定位。

步骤5：以上步骤任意一步成功即可得到当前帧的位姿的初始值。利用该值，将局部地图点全部投影至当前帧进行匹配，匹配完成后进行局部优化同时剔除误匹配点(图2(b))。统计正确匹配点数，若大于20则判定为成功，若小于20判定为失败，传入下一帧，执行步骤4。

2.3 关键帧选取

正确跟踪当前帧之后，判断当前帧是否作为关键帧。本文的全景影像框幅高达8000×4000像素，由于车辆高速行驶，存在内存读写的限制，因此采用较大的采样间隔(1～3 m)。判别当前全景影像为关键帧的条件为满足算法2列表中的任意一点。

算法2 关键帧选取的判别规则

(1) 超过8帧未插入关键帧，则确定当前帧为关键帧。

(2) 当前帧新插入的地图点大于其跟踪到的地图点的1.7倍。

(3) 当前帧跟踪到的地图点数小于上一帧跟踪到的点数的85%且局部地图构建线程空闲。

(4) 当前帧跟踪到的地图点数小于上一帧跟踪到的50%，中断局部地图构建并插入关键帧。

(5) 局部地图构建(local mapping)线程空闲。

2.4 局部地图构建

当局部地图线程检测到新插入的关键帧后，首先应更新当前关键帧的连接关系，找出与其具有一定共视点数的关键帧作为共视关键帧。根据全景相机的特殊情形，本文设定共视关键帧必须同时满足：① 与当前关键帧的共视点数≥50个；② 与当前关键帧在图像序列中的间隔关键帧不超过40个；③ 其与当前关键帧的共视点在两帧所在金字塔层数差异>2的特征点数不超过总共视点数的85%。

2.5 闭环探测与全局优化

使用词袋模型进行闭环探测的技术较为成熟，本文使用文献[28，31]提出的闭环探测方法，利用ORB特征点结合DBoW2库进行闭环探测，流程如算法3所示。

算法3 闭环探测流程

检测到新关键帧插入：

(1) 计算当前关键帧的BoW向量，用于表示当前帧的场景信息。

(2) 通过相邻关键帧计算相似性阈值。

(3) 通过关键帧相连关系计算相似性累计得分，结合2的阈值选取闭环候选帧。

(4) 连续性检验：认为孤立的候选组具有很强的不确定性。

(5) 通过连续性检验的候选关键帧均认为与当前帧构成闭环。

闭环关键帧选取完毕后，依次与当前关键帧使用BoW搜索匹配特征点，若匹配点数小于30，则剔除此闭环关键帧，继续下一帧的匹配。匹配成功后，按照文献[32]的方法计算闭环帧到当前帧的相似变换群，即sim(3)变换，此时便得到了闭环关键帧与当前帧的转换关系S，通过转化关系再次搜索匹配点并使用局部光束法平差优化S。最后，调整当前帧及其相连关键帧的位姿与地图点，更新关键帧链接关系并传递调整位姿，构建Essential Graph进行全局位姿优化(图2(c))并调整相应地图点。

3 试验结果和分析

3.1 试验设计

本文试验选取了两组数据均采集自车载Ladybug3相机，分别称为Kashiwa和Omiya图像序列。Ladybug拍摄鱼眼影像大小为1616×1232像素，像元分辨率为0.009 mm，颜色分辨率为8 bit量化的RGB色彩空间。鱼眼相机的焦距为3.3 mm，投影中心相互距离约40 mm；共有6个鱼眼相机，5个相机用于360°水平成像，1个相机指向天空。全景影像球面成像于距离球心20 m处。拼接后的全景影像大小为4000×2000像素。

Kashiwa图像序列包含498张全景影像，摄影间隔约2 m；Omiya图像序列包含7464张全景影像，拍摄间隔约为1 m。由于天空上没有特征点，匹配在独立的水平鱼眼相机中执行，而F矩阵计算、光束法平差都是在统一的全景坐标系中进行。参考值由高精度的GPS/IMU组合导航系统获得，且GPS经过CORS站的事后改正，其绝对定位精度高于10 cm。GPS/IMU数据不参与SLAM流程。本文同时采用两种精度评价方法进行评价，首先按照经典的SLAM算法，给定初始位置，姿态与尺度信息将相对位姿统一到给定的坐标系下，之后不再给出任何控制信息，并计算绝对定位均方误差以衡量SLAM系统的实时动态定位精度。考虑到在测绘中的应用，全局定位精度更受关注，因此本文选取均匀分布的少量GPS点作为控制点，根据7参数相似变换将所有的SLAM后得到的外方位元素转换到绝对坐标系中，并计算所有相片外方位元素与参考值间的绝对值，作为精度评定指标。本文的SLAM系统运行在Ubantu16.04环境下,使用Qt5.8作为集成开发环境。CPU为Intel Core i7-7700HQ@2.8 GHz，内存为8 GB，执行效率约每秒1帧。

3.2 试验结果和分析

3.2.1 相机检校结果

表1比较了全景相机中鱼眼镜头的检校结果。采用63个均匀分布的校准点，根据不同的检校模型，解算对应的模型参数，并评估了检校中误差。本文方法的精度为0.56像素，明显高于文献[33]提出的通用相机检校模型，并后继保证了优于一个像素的核线精度。

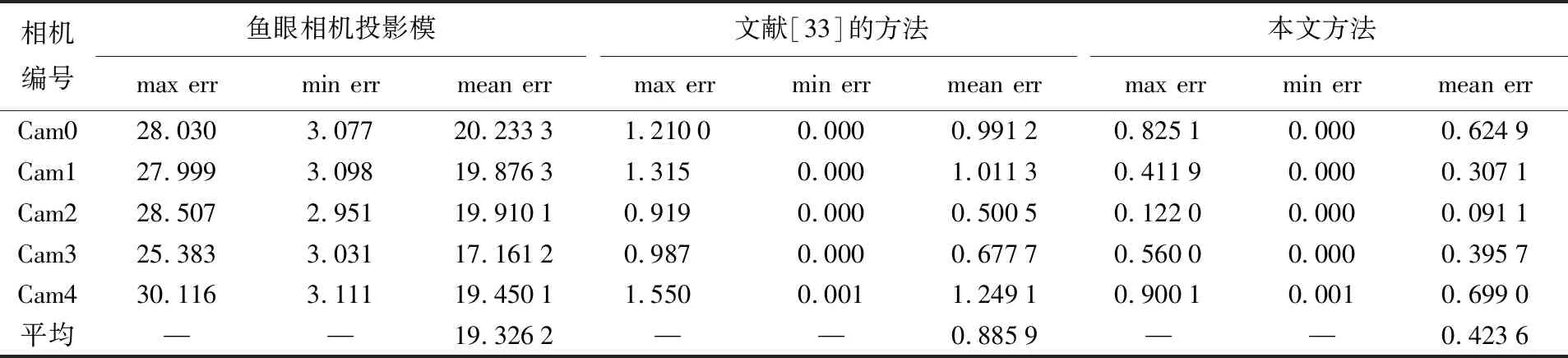
表1 本文使用的鱼眼相机检校方法检校结果与文献[33]对比

3.2.2 特征提取与匹配结果

图3所示为Ladybug数据集使用三帧同时匹配的结果，由于鱼眼相机变形较大，距离相机越近的地物变形越大，可以看出，特征点基本分布于距相机相对较远的地物上。图中3号相机只匹配出了极少的特征点。这表明基于单相机SLAM容易受到匹配条件的困扰而追踪失败。而本文使用的多镜头组合式全景相机可依赖其余镜头捕捉到的足够的特征点完成跟踪和后继平差。此外，由于本文根据几何关系设定了恰当的搜索区间(算法1)，0号相机和4号相机的同名点也能够进行正确匹配。

图3 连续三帧图像所匹配的ORB特征点Fig.3 Matched ORB features on three adjacent frames

3.2.3 闭环探测结果

如图4所示，蓝色连线表示所探测的闭环，Kashiwa数据集共探测出52个闭环，Omiya数据集共探测出203个闭环。在SLAM系统中，一旦成功探测出闭环，将进行相似变换关系的计算，传播位姿并更新连接关系，连接关系更新后，便可避免重复的路径中对于冗余的闭环探测过程(蓝线所示)，重复路径中的关键帧将更新与先前帧的相连关系，并统一参与位姿图的优化。

3.2.4 定位结果

表2为Kashiwa和Omiya图像序列使用全景SLAM跟踪所得位姿精度。仅用前两帧的GPS、IMU数据作为SLAM轨迹的对齐，其他所有的GPS/IMU数据作为参考和精度评价。Kashiwa序列(1 km，498张全景影像)定位平均精度达到30 cm。Kashiwa序列具有很好的共视条件，不使用闭环纠正其精度依旧能达到46 cm。Omiya序列(9 km，7492张影像)仅在图4所示处存在闭环，且运行里程较长，因此闭环约束的范围有限，无闭环纠正精度为42.7 m，加入闭环后精度为19 m。

事实上，在测绘中更加关注静态的全局定位精度，而非机器人领域的动态当前定位精度。因此本文分别在Kashiwa与Omiya图像序列上分别加入3个与15个均匀分布的GPS控制点进行7参数转换与整体平差，将SLAM轨迹纳入到绝对坐标系下，并统计更符合实际应用的定位精度。如表3所示，两套数据集的定位精度分别达到13 cm与16 cm。在角度上，车辆的姿态基本仅在水平方向上有旋转，误差主要集中在水平旋转角Rz上。

表2 Kashiwa图像序列与Omiya图像序列数据集使用全景SLAM跟踪所得结果，仅用前两帧GPS/IMU数据对齐SLAM轨迹

Tab.2 Pose and map point location accuracy of the trajectories of Kashiwa and Omiya sequences, aligned by the given initial pose and scale

数据定位中误差/m地图点残差/m位置/m姿态/(°)DxDyDzRxRyRzKashiwa加闭环0.30340.77200.14000.23220.01000.620.743.75无闭环0.46420.85430.47220.49110.01050.650.854.77Omiya加闭环19.529625.138414.231412.72644.11221.252.143.85无闭环33.058640.240620.990124.05798.57333.912.463.21

表3 Kashiwa图像序列与Omiya图像序列使用全景SLAM跟踪所得结果，用最小数量均匀分布的GPS点7参数变换对齐SLAM轨迹

Tab.3 Pose and map point location accuracy of the trajectories of Kashiwa and Omiya sequences, minimum number of even distributed GPS points are used to align SLAM trajectories

数据定位中误差/m地图点残差/m位置/m姿态/(°)DxDyDzRxRyRzKashiwa加闭环0.13400.30050.07860.108 0.01020.610.743.23 无闭环0.15680.32780.10570.11540.01020.620.813.01 Omiya加闭环0.16380.69690.11210.09990.00010.120.332.85 无闭环0.16810.73500.13540.09970.00010.910.461.991

特征法SLAM可得到稀疏地图点云，如图5所示。由于没有实际的控制点评价物方定位精度，本文采用误差传播的方式，利用摄站定位误差估计物方点误差。表2中的地图点残差是与GPS/IMU作为真值前方交会出的地图点坐标进行比较的结果。

图5给出了Kashiwa与Omiya序列的使用全景SLAM系统得到的全局地图全览(包括关键帧的位姿及其连接关系与地图点分布情况示意图)，图中Kashiwa序列(图5(a))当前帧为接近终点的第492帧，在无闭环纠正的情况下，尺度的漂移非常小。这归功于全景相机的360°成像。图5中绿色的线条显示了关键帧的连接关系，同时也是位姿优化中重要的图连接关系。

图6表示通过给定初始位姿态与方向，将SLAM的轨迹通过7参数转换到地理参考坐标系下与GPS的轨迹对比。其中，蓝色曲线为GPS参考位置，红色曲线为全景SLAM所跟踪出的位姿结果。可以看出，Kahiswa序列由于极好的共视关系，跟踪定位位置与GPS参考位置近乎完全重合，Omiya序列由于运行里程较长、共视关系较差且无较好的闭环约束，出现了一定程度的尺度漂移。然而，在加入极少量(15个)控制点后，定位精度变具有明显的改善，与GPS参考轨迹一致(图6(d))。

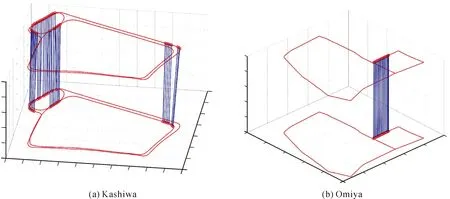
图4 两套数据集上所探测出的闭环Fig.4 Detected loops on two datasets

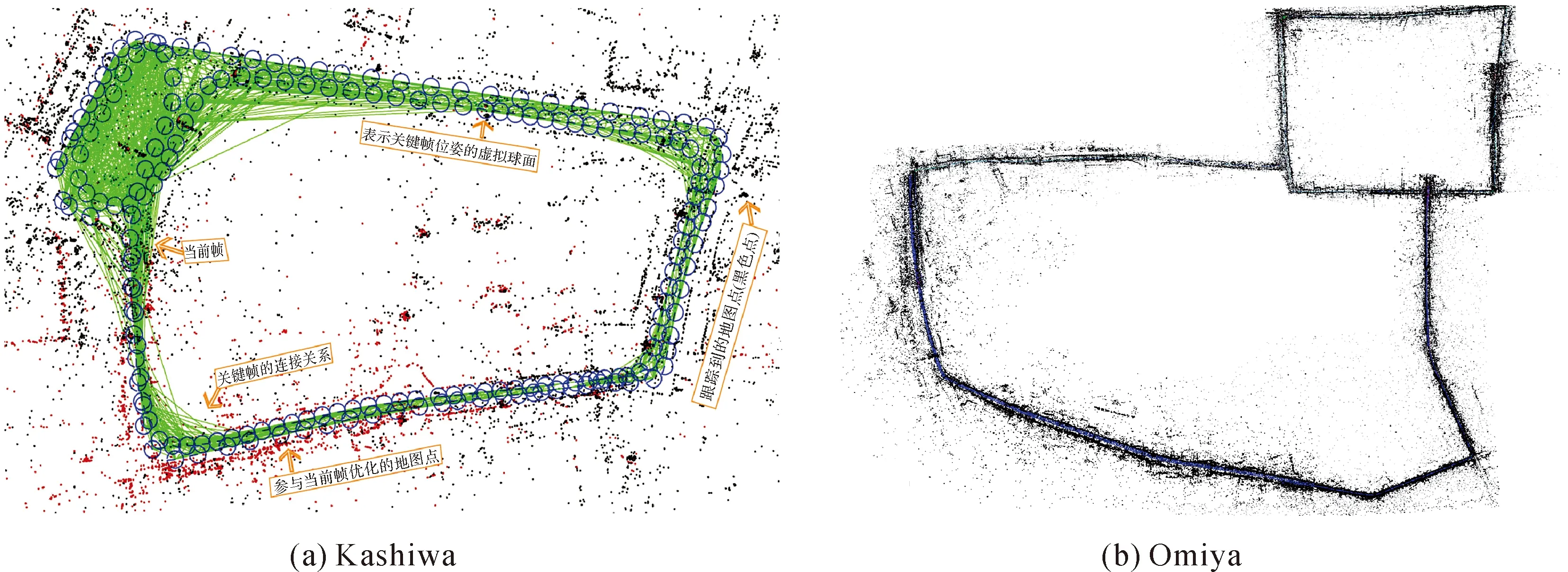
图5 Kashiwa与Omiya序列使用全景SLAM系统跟踪后得到的全局地图总览(关键帧及其连接关系，地图点分布情况)Fig.5 Overall of global map of Kashiwa and Omiya sequences by panoramic SLAM system (status of current frame, tracked map points, tracked key frames and their connections)

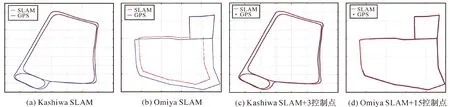
图6 两个区域的SLAM结果以及加入3/15个控制点后的定位结果分别与GPS参考的对比Fig. 6 The comparison between GPS reference and SLAM results before and after GCP alignment

3.3 待改进之处

本文采用BoW词袋模型并参考ORB-SLAM闭环探测的方法对全景图像序列进行闭环探测。文献[34]指出在复杂场景中闭环探测具有相当的难度，ORB-SLAM使用的闭环探测方法具有很大的局限性。这在全景SLAM中问题更加突出。如图7所示，除了球面投影形变，地面物体的分布也发生了剧烈的变化。不过，归功于全景相机的大范围视场，未加入闭环约束的位姿跟踪已可达到较为满意的效果。

图7 反向行驶拍摄的全景图像Fig.7 Two panoramic images shot in the reverse directions

4 结束语

本文提出了基于多镜头组合式全景相机的全自动SLAM系统。该系统能够实现全景图像系列的定位和稀疏地图重建，其定位精度接近GPS参考精度。相对于国际上主流的基于传统平面相机的各类SLAM系统，如Mono-SLAM、Stereo-SLAM以及RGB-D SLAM，本文提出的全景SLAM可作为良好的补充，辅助或取代昂贵的GPS/IMU导航系统，特别是在GPS信号失锁时。后期的工作将集中于全景相机影像的闭合探测，以增强几何约束，得到更好的定位精度。