基于多元逐步回归模型的物质浓度测定方法
2019-10-29童强
童强
(兰州石化职业技术学院信息处理与控制工程学院,甘肃 兰州 730060)
1 原始数据
表1为二氧化硫在不同浓度下的R、G、B、S、H颜色值。
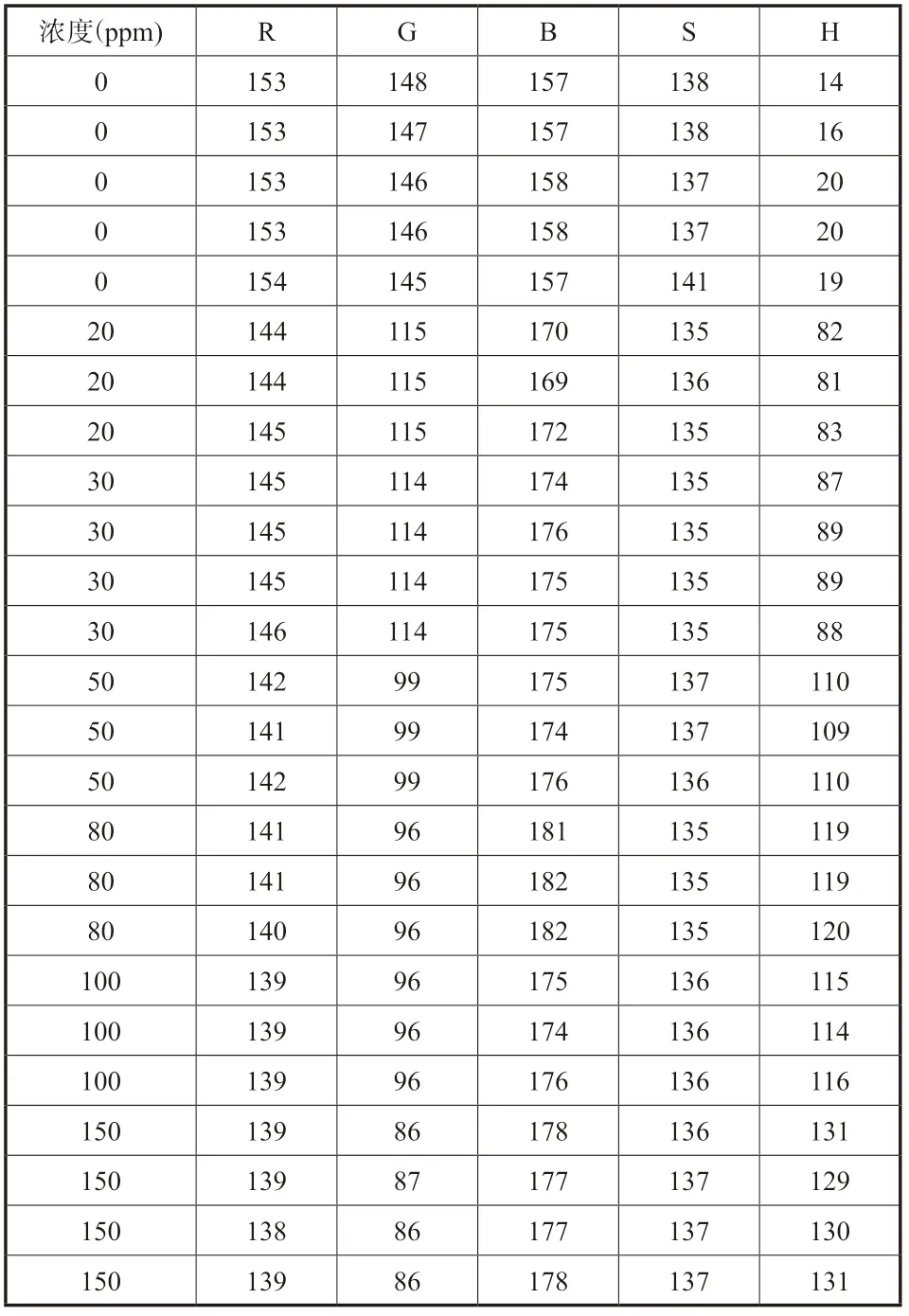
表1 二氧化硫-各浓度下的颜色值
2 基于多元逐步回归的浓度测定模型
进行多元回归时,有些变量是可以剔除的,为此采用matlab进行逐步回归[1]。MATLAB代码如下:
clear;clc
C=[153 148 157 138 14
153 147 157 138 16
153 146 158 137 20
153 146 158 137 20
154 145 157 141 19
144 115 170 135 82
144 115 169 136 81
145 115 172 135 83
145 114 174 135 87
145 114 176 135 89
145 114 175 135 89
146 114 175 135 88
142 99 175 137 110
141 99 174 137 109
142 99 176 136 110
141 96 181 135 119
141 96 182 135 119
140 96 182 135 120
139 96 175 136 115
139 96 174 136 114
139 96 176 136 116
139 86 178 136 131
139 87 177 137 129
138 86 177 137 130
139 86 178 137 131
];Y=[0 0 0 0 0 20 20 20 30 30 30
30 50 50 50 80 80 80 100 100 100
150 150 150 150]’;stepwise(C,Y)
程序执行后,显示如图1的逐步回归初始界面,可以看到当前的回归情况、R2值、F_检验值和p值等。
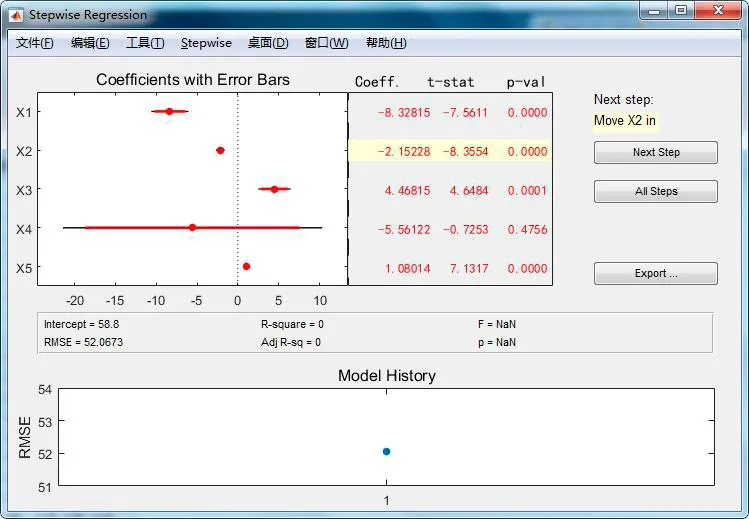
图1 逐步回归初始界面
点击“Next step”按钮后,加入X2(即G颜色维度值)进行拟合,显示如图2。

图2 提示加入X4变量
再次点击“Next step”按钮后,自动加入X4(即S颜色维度)进行拟合,显示如图3。

图3 提示逐步回归结束
此时,提示“Move no terms”,即:没有要移除的或要加入的变量了,此时蓝色显示的是被保留的有效行(有效变量维度),红色显示的是被剔除的行(变量维度)。由此得到逐步回归模型:
y=-11.735g-5.04823s+1802.64
而且可以看出,R2=0.882855,说明模型拟合得很好,F_检验值=82.9004>0.000,且与显著性概率相关的p值=5.70133e-11<0.05,从图中可以看出RMSE(标准误差)也不太大,这说明逐步回归效果很好[8]。
鼠标点击蓝色的两行后,相应行变红,此时实际上是所有行(变量维度)都未加入,点击第一行(第一个维度)使其加入,显示如图4。
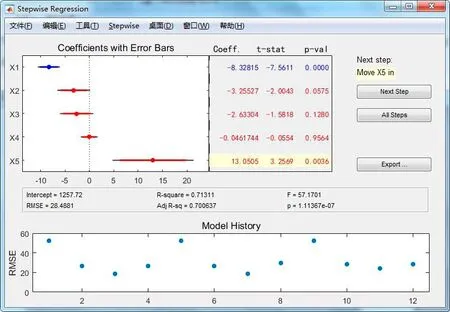
图4 提示加入变量X5
点击“Nextstep”按钮后,自动加入X5(即H颜色维度)进行拟合,显示如图5。
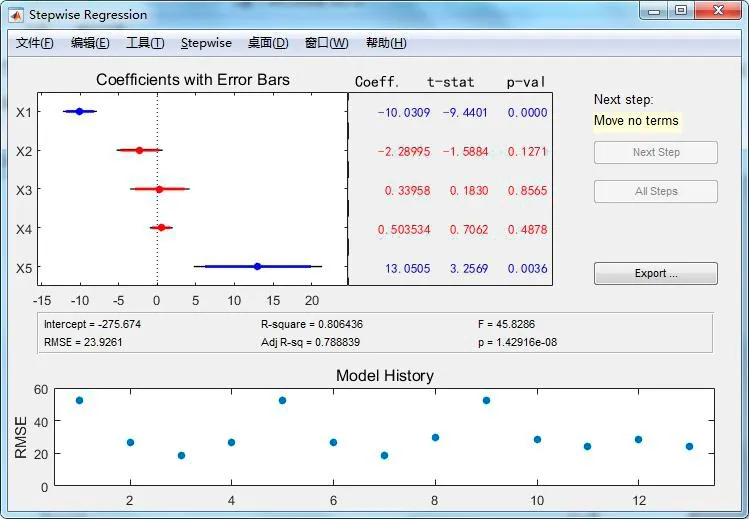
图5 提示逐步回归结束
此时,逐步回归执行结束,由此得到另一个逐步回归模型:
y=-10.0309r+13.0505s-275.674
而且可以看出,R2=0.806436,说明模型拟合得很好,F_检验值=45.8286>0.000,且与显著性概率相关的p值=1.42916e-08<0.05,从图中可以看出RMSE(标准误差)也不太大,这说明逐步回归效果也很好,但不如上一个逐步回归模型好。
3 结语
本文基于多元逐步回归模型得到了较好的颜色读数与物质浓度关系模型,可用于物质浓度的快速测定。
