江海直达船深浅水绕流场数值模拟方法研究*
2019-10-29张元浩秦江涛李子如
张元浩 秦江涛 李子如 贺 伟
(武汉理工大学交通学院 武汉 430063) (高性能舰船技术教育部重点试验室 武汉 430063)
0 引 言
在船舶大型化发展趋势下,部分内河航运船舶面临的限制水深问题更为突出[1].船舶航行于浅水航道会导致浅水效应[2],其中浅水效应对船舶阻力方面的影响包括: ①由于水域受限,船体底部与河床之间形成狭窄的流道,导致船底的流速增大,从而增加了船舶阻力;②流速的增加引起船底压力降低,导致船体发生明显的下蹲,除增大湿表面积增加阻力、改变航态影响阻力外,在剩余水深较小时更易发生触底的安全事故[3].因此,浅水效应问题是内河航运需研究的重要课题[4].
近年来计算流体力学(CFD)方法越来越多的应用于船舶水动力性能研究[5].其中在考虑船舶航态的绕流场数值模拟中,由于航态未知从而是数值模拟的待求解变量.对于静水航行船舶的航态求解,通常基于船体受力/力矩平衡根据刚体运动方程调整船体升沉与纵倾[6],在调整后的航态下再次进行流场的数值模拟至收敛,并重复以上步骤直至航态稳定.
由于船舶航态的改变,导致船体与水面、航道底部的相对位置随之变化也即影响到了计算域的形状,对于计算域形状改变的实现在数值模拟中通常采用两类解决方法.
1) 动网格方法 采用动网格处理船舶航态问题的方法包括网格变形、重叠网格以及动域方法.
网格变形方法中,由于船体姿态改变,船体运动导致与之相连的体网格变形,数值模拟中通常结合弹簧光顺、扩散光顺模型等动网格技术实现计算域离散网格的变形,该方法在网格质量较差的位置会辅以网格重构技术以避免变形后的网格质量较差.孙树政[7]采用网格变形方法进行了某深V型船型典型横剖面的水动力导数数值预报;倪崇本[8]采用网格变形方法实现了计及航行姿态变化的三体船阻力数值预报.
重叠网格方法将计算域划分为不同的子域,各子域的网格独立生成,彼此嵌套重叠,不同区域的网格通过插值实现流场信息的交换[9].吴明等[10]采用重叠网格方法,数值模拟了S60船舶浅水绕流场,其研究中数值结果与试验结果吻合良好;骆婉珍等[11]采用了动态响应运动模型结合重叠网格技术对某内河巡逻艇的航态与阻力进行数值预报,认为该方法可准确预报船体在浅水中的阻力与波形.
采用流体域运动的方式则将整个计算域作为刚体,计算域随船体运动而运动,由于该方法中的计算域仅发生位置的改变而形状维持不变,因此整个计算域的离散网格形状以及相对位置也不发生改变.易文彬等[12]针对DTMB5415船,采用STAR CCM+的DFBI刚体运动模型通过控制域运动的方式实现了计及航态的船模阻力及绕流场数值预报.
2) 重新建模方法 重新建模方法中航态求解与动网格方法一致,根据所求解的船舶姿态,调整船舶在计算域中的位置并对新计算域重新进行网格离散,随后通过上述方法的不断迭代获得船舶的最终航态以及流场.董文才等[13]运用重新建模法计算某深V型船中高速航行时的航态与阻力,阻力与航态的计算结果与试验结果相差在5%以内.
在前述四种网格方法中,网格变形方法通过引入网格光顺模型实现船体运动后的网格变形与运动,在船体航态变化较大时易导致部分区域动网格质量变差甚至导致数值模拟发散;控制域运动的方法则需施加合理的边界条件,通常船体前方与侧面、上下表面均采用给定来流速度的边界条件,但该方法不适用于浅水航道底部边界—由于航道底部为固壁,而该方法的边界随同计算域运动导致与来流呈一定夹角,从而违反了壁面不可穿透条件.采用重叠网格与重新建模的方法既能避免了计算域运动方法中浅水航道底部与来流的非物理夹角,也可避免船体运动对网格结构的影响.
文中借助CFD软件STAR CCM+对一江海直达船的深、浅水绕流场进行了数值模拟,对比了重新建模法与重叠网格法两种网格方法在低速肥大船深浅水绕流场数值模拟的特点.
1 数值模拟方法与验证
对江海直达船深浅水绕流场进行数值模拟前需保证数值方法的有效性,以KVLCC2船模(具体船型参数与试验参数见文献[14])无限水深绕流场为对象.通过数值模拟预报了船模阻力、航态等流场信息,并结合试验结果分析了数值方法的有效性.
1.1 数值方法
1) 控制方程 黏性绕流场的流体遵循流体力学的质量守恒定律与动量守恒定律,文中通过数值求解不可压连续方程与RANS方程组的方法进行船舶绕流场数值模拟.控制方程的表达见文献[15].
2) 湍流模型 由于对NS方程取时均所得的RANS方程中出现雷诺应力项导致方程组不封闭.采用标准k-ε湍流模型进行雷诺应力的模拟.
3) 近壁面处理与壁面函数 由于黏性作用,近壁面流动的切向速度等流动参数沿边界层法向变化较快,同时近壁面的流动通常是重点关注的研究对象,因此近壁面流动的准确捕捉对有物面边界限制的湍流模拟至关重要.对近壁流动的处理采用壁面函数方法[15],该方法减少了近壁区域对网格密度的要求,从而减少网格数量并提高数值模拟的效率.
4) 自由面处理 数值模拟中对自由面的处理采用VOF捕捉方法,同时采用HRIC(high-resolution interface capturing)格式[16-17]来处理不混合组分的对流输运方程.
5) 航态预报与调整 基于船体垂向受力与纵倾力矩平衡求解船舶运动方程,其中运动方程的求解采用一阶欧拉显式方程,并引入亚松弛因子α(0>α>1)来调节航态的改变量:

在航态求解基础上,分别采用重叠网格法(overset mesh)和重新建模法(rezone & remesh)实现数值计算中航态的调整[18].文中借助二次开发脚本程序完成重新建模法的计算域建立与网格离散,解决了人工介入工作量较大和多次网格划分的布置与尺度的一致性问题.
6) 计算域与边界条件 假定船舶绕流场关于中纵剖面对称,因此数值模拟以半个流场为对象,水深取为25倍船舶吃水并假定此水深无浅水影响.边界条件设定与位置见表1.

表1 计算域的设置
7) 离散网格 船体近域采用棱柱层网格,其他区域采用Cutcell网格.为精确捕捉自由表面以及船体附近的流场,采用六面体密度盒在自由面与船体附近进行局部加密,计算域内网格见图1.在采用重叠网格法时,将计算域划分为图2的两个子域,两个子域的网格单独生成.
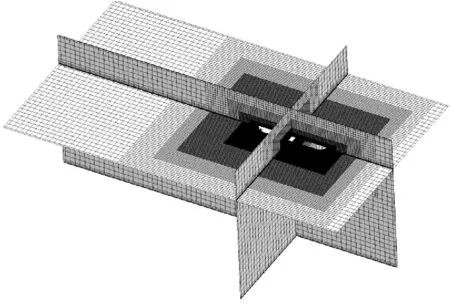
图1 计算域典型剖面网格分布图

图2 重叠网格方法区域划分示意图
1.2 阻力数值结果不确定度分析


表2 网格数量
不同网格密度的数值模拟结果与MOERI水池船模试验结果[14]见表3.
总阻力系数数值结果不确定度分析的各项参数如表4所示.
从表4可见,收敛因子0 表4 阻力系数不确定度分析 采用中密度模型的网格尺度对KVLCC2船不同傅氏数的绕流场进行了数值模拟,数值结果与MOERI水池船模试验结果见图3. 图3 数值及试验结果 KVLCC2船模深水绕流场数值结果与试验结果基本吻合,其中阻力数值结果的相对误差在3%以内,数值方法具有较高的准确性. 数值模拟对象为双机双桨的江海直达低速肥大型船,船模试验与数值模拟对象为缩尺比21.111的模型,江海船的主要船型参数见表5. 表5 江海直达船实船的主要参数 江海直达船的三维模型图见图4. 图4 江海直达船三维模型图 船模试验和数值计算的水深包括无限水深(H/T=25)与浅水(H/T=3,H/T=2),Fr分别为0.126,0.133,0.140,0.147,0.154和0.161. 本节数值模型与数值方法与第1节一致,仅在浅水绕流场数值模拟中计算域底部边界与船体的距离根据水深调整. 江海船计算域的离散网格采用与KVLCC2数值模拟相同形式的密度盒进行加密.计算域内离散网格数量见表6. 表6 深浅水计算域离散网格数量 2.3.1阻力与航态 江海直达船深浅水绕流场数值模拟阻力和航态的数值结果及模型试验结果见图5. 图5 数值与试验结果 由图5可见,总阻力系数,下沉量与纵倾角随水深变浅与Fr增加而增大.整体而言,总阻力系数的计算结果与试验结果吻合较好,最大误差在4%左右;航态的计算结果受水深的影响较大,其中在最浅水深(H/T=2)重新建模与重叠网格升沉数值结果的最大相对误差分别为11.48%与12.23%;纵倾数值结果的最大相对误差分别为11.19%与8.69%. 采用来比较两种方法与数值结果与试验结果的吻合程度: 表7 不同网格方法数值结果 % 2.3.2兴波波形与压力分布 图6 船底压力分布图 数值结果显示,两种方法捕捉到的船体表面压力分布较为相似:前肩部与双尾鳍之间形成低压区,且船体压力降低首尾低压区幅值与面积随着水深变浅呈现增大的趋势. Fr=0.154的江海直达船深浅水绕流场自由面波形的数值结果见图7.其中:Z/Lpp为波高与船长的比值. 图7 自由面波形图 由图7可知,横波幅值随水深变浅而增大,以前肩部最为明显,横波长度随水深变浅逐渐变长.当H/T=2船舶航态变化剧烈,增加了重叠域与背景域之间插值传递信息的难度,受此影响,图7c)中重叠网格法的自由面波形图未能反映散波的波形细节. 2.3.3数值计算效率对比 数值方法收敛性是影响计算效率的重要因素,研究发现,计算同一工况时,重叠网格法达到收敛标准需要的物理时间与重新建法相差不大,图8为两种网格方法在计算同一工况的总阻力收敛时历曲线. 图8 江海船总阻力收敛时历曲线对比(H/T=2,Fr=0.154) 由于重叠网格方法在重叠区域采用两套网格,采用相同的网格加密方式时重叠网格法需多使用一半以上的网格(江海船离散网格数量见表6),所以每迭代一次需要更长时间,重叠网格法数值计算的效率较重新建模方法要低,表8为相同计算平台下两种网格方法模拟Fr=0.154工况绕流场达到收敛标准所需的墙钟时间. 表8 数值模拟墙钟时间 由表8可知,重新建模方法比重叠网格法节约30%以上的计算时间. 1) 浅水效应对江海直达船的影响如下:总阻力系数随着水深变浅显著增加,下沉量与艏倾增大;横波幅值与散波长度随水深变浅增加;船底受浅水回流影响,低压区明显增大. 2) 比较重新建模法与重叠网格法对阻力与航态的计算结果,两种方法的计算结果的平均误差未见明显差异,可认为具有相当的数值精度. 3) 重新建模法与重叠网格法对深浅水压力分布的模拟结果相差不大,但是重叠网格法波形捕捉能力更易受到水深变化的影响. 4) 在近似的网格尺度、密度与布置情况下,重新建模法的比重叠网格法具有更高的数值模拟效率.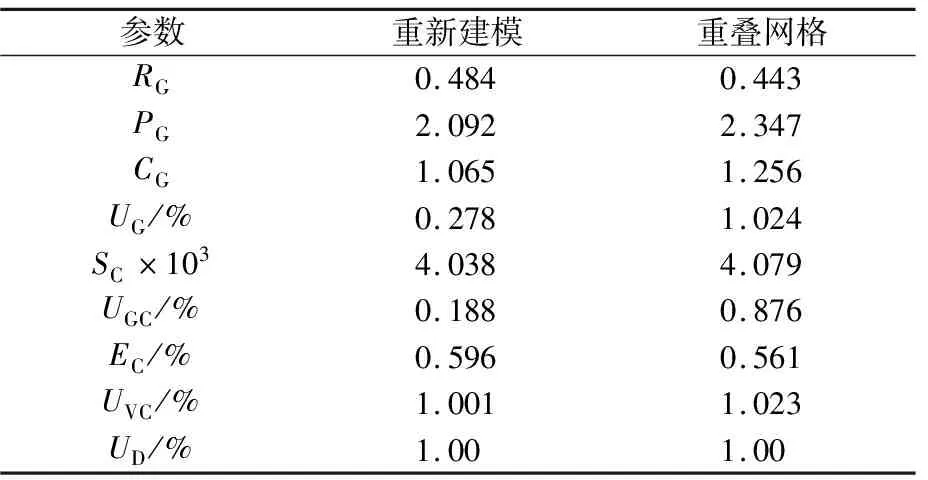
1.3 数值结果的准确性
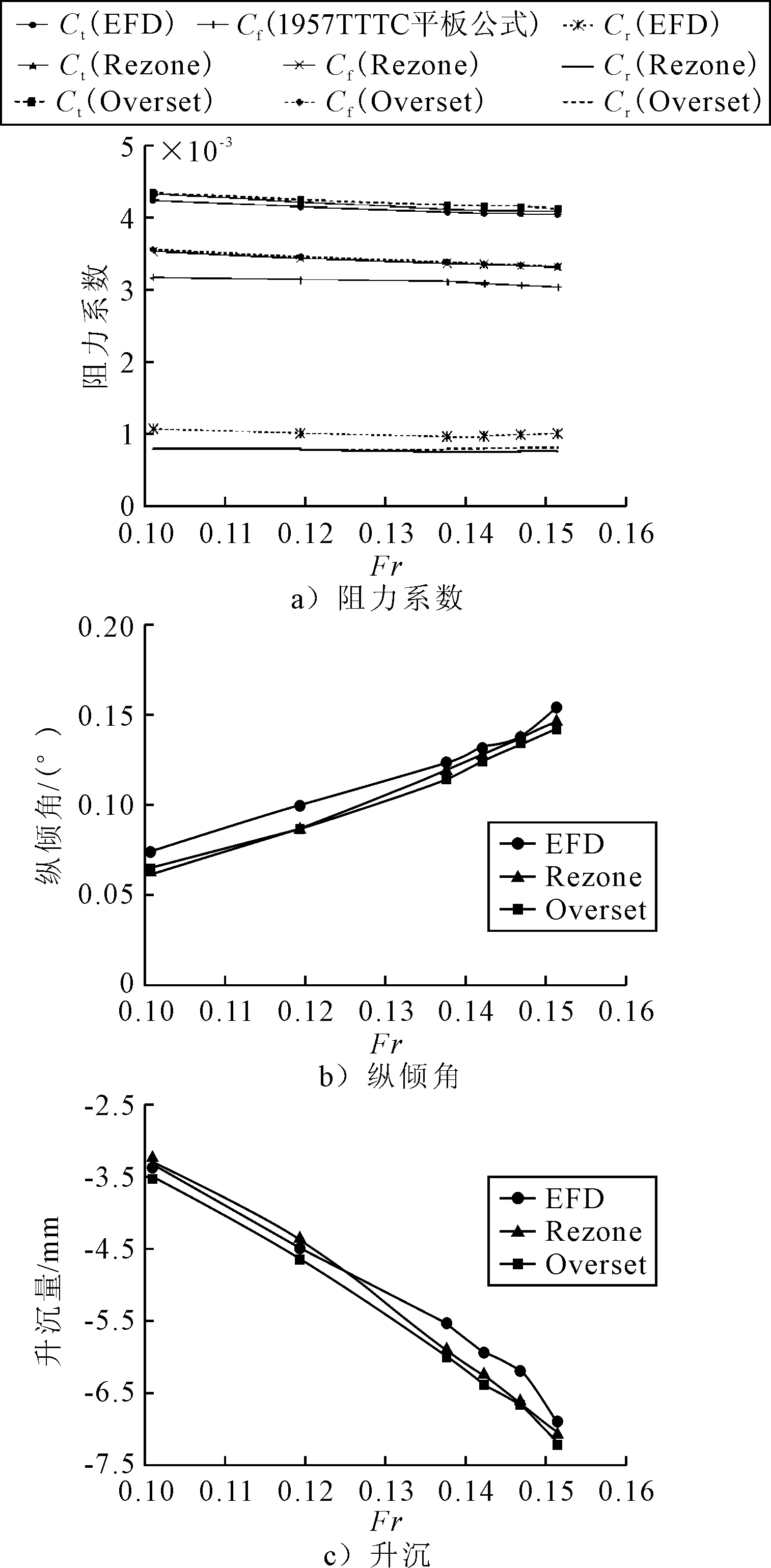
2 江海直达船深浅水绕流场数值模拟
2.1 船型对象


2.2 数值模型与工况

2.3 数值与试验结果






3 结 论
