模糊环境下基于双向流通的城乡物流配送研究

姚冠新　吴娟　朱晨俊　戴盼倩

内容摘要：本文构建了农产品进城、消费品下乡的城乡双向物流配送模式。在供需不确定的环境下，文章采用三角模糊数表示不确定环境，并综合考虑了配送总费用、客户时间满意度和车辆空载率，从而建立了双向流通的城乡共同配送的多目标优化模型，并通过遗传算法求解算例，最后比较分析结果。结果表明，文章所建立的模型是有效的，能够为城乡双向流通的配送优化决策提供理论依据和实践指导。

关键词：不确定环境   城乡双向流通   物流配送   遗传算法

随着城乡一体化的发展，我国城市和农村的经济联系更加紧密，城市和农村之间的交通条件得到极大改善，其带动了城乡之间物流的发展，实现了农产品进城、工业品与消费品下乡，从而促进了城乡经济发展。但是据相关研究表明，在城乡商品物流过程中，车辆往返途中同时实现两个流通过程的情况很少，其基本以单向运输为主，车辆空载率较高，这就造成了运输成本的极大浪费。王素仙（2017）、贺珺玮（2018）等对流通体系构建做了初步的战略框架;秦星红（2011）以重庆市为例提出以生产加工企业为中心和连锁经营方式为框架的城乡双向物流模式;而对于城乡配送优化问题上，彭永涛（2016）以变分不等式的方法和GAMS软件对城镇的配送网络进行优化求解;卢美丽（2012）用混合整数规划的方法对连锁超市配送问题进行研究。本文为降低车辆空载率，同时考虑到客户时间满意度和配送总费用，对双向流通的农产品的配送网络进行优化研究。

双向流通的城乡物流配送网络模型构建

（一）问题描述及假设

本文构建的是一个配送中心、多个农村节点、多个城市节点构成的物流网络。整个配送模式为配送中心车辆到达各农村需求点，在需求点完成消费品的卸货和农产品的装载，农产品全部装载完毕后，车辆将农产品分别配送至各城市需求点，最后返回配送中心。应该注意的是，在这种配送模式中车辆的装货和卸货是在同一地点完成;运输的消费品和农产品可以混合，也就是说所有商品都可由同一辆货车运送。

基于上述问题，本文提出以下假设：

农村需求点和城市需求点的需求量不确定，为模糊随机变量;农村点有足够的农产品供给能力;配送中心与各需求点的位置已知，各点之间的路径是直线，即两点之间的距离为 ;车辆的最长运输距离和最大负载能力是已知的，并且每条运送路线的总长度不超过车辆的最长运输距离，车辆离开每个需求点时的货物载荷不超过车辆的最大载荷能力，即在运输期间中不允许车辆过载;每条路线的开始和结束位置都是配送中心，每个需求点的服务都能够被满足，且只能访问一次，不允许分车分批配送和装载;如果车辆未在需求点要求的时间窗内完成服务，会产生相应的惩罚费用。

（二）模型構建

1.参数介绍。I={i|i=1，2，3，…，m} 表示m个农村需求点的集合;J={j|j=1，2，3，…，n}表示n 个城市需求点的集合;V={v|v=1，2，3，…，k} 表示k辆货车的集合;为了简化模型，农村和城市需求点统被视为客户节点，因此G={0，1，2，3，…，m，m+1，…，m+n}，表示所有点的集合，其中0表示配送中心，{m+1，…，m+n}表示城市需求点;dab表示点a 到点b 的距离，a，b∈G;Dv表示每辆货车行驶的最大距离;qi表示农村需求点i 对消费品的需求量，是模糊变量，i∈I ;q j表示城市需求点j 对农产品的需求量，是模糊变量，j∈J ;Pi表示农村节点的农产品供给能力，i∈I;pi表示各农村节点农产品取货量，i∈I;Qv表示货车的最大载货量;C1表示单位车辆单位距离运输成本;C0表示车辆启用的固定成本;1表示在时间窗之前到达而产生的单位时间等待成本;2表示在时间窗之后到达而产生的单位时间惩罚成本;ta表示车辆到达需求点a 时间，a=1，2，3，…，m，…，m+n ;[Ea，La]表示需求点a 要求的服务时间窗， a=1，2，3，…，m，…，m+n;Wo表示车辆离开配送中心的载货量;Wi表示车辆离开农村需求点i的载货量，i∈I;

2.目标函数。客户时间满意度。在时间窗最小值Ea 之前将货物送达某需求点，则满意度为1;在时间窗最大值La之后达到则满意度为0，若介于时间窗之间达到，那么客户满意度随送达该需求点时间的增加而递减。

式（6）表示农村节点的农产品供给能力能充分满足城市节点的需求;式（7）表示车辆离开配送中心时的载货量;式（8）-（10）表示每个客户节点只能有一辆车为其服务，每条运输路线只有一辆货车进行服务;式（11）车辆从配送中心出发，完成任务后返回配送中心;式（12）-（14）表示货车在整个运输路途中不存在超重;式（15）-（16）车辆运送顺序为配送中心，农村需求点，城市需求点，最后再返回配送中心;式（17）表示每辆货车运输路线的行驶距离不超过其最大行驶距离。

模型转化及求解

（一）约束条件的转化

设r和u分别为模糊数的下限和上线，s为可能性最大的值，那么模糊数用（r、s、u）来表示，Lai Y J和Hwang C L考虑三种模糊情况提出了多目标线性规划模型，用来求解具有模糊目标以及模糊约束系数的线性规划问题，对于本文中涉及的模糊情况即 其中ω1，ω2，ω3， 分别表示模糊数的下限、可能性最大值及上限的权重，β为最小可接受度，并分别给出 ω1=1/6，ω2=2/3，ω3=1/6，且β=0.5。因式（6）-（7），式（12）-（13）的约束可以分别转化为：

（二）多目标转化单目标

多目标转化单目标的方法主要为线性加权求和法，平方加权法，主要目标法等。本文采用线性加权求和法求解。但由于本文的三个目标量纲不一致，因此需要做无量钢化处理，本文用极值化方法对变量进行处理。客户满意度、配送总费用和空载率进行无量钢化处理之后分别为：

（三）模型求解

本文多目标优化求解的过程如下：第一，约束条件的清晰化，将带有模糊参数的约束条件通过文献9的方法转化为确定性的约束条件;第二，将量纲不同的三个目标式（1）（3）（5）进行归一化，采用最大值方法进行无量纲化处理分别转化为式（22）（23）（24），最后结合目标权重进行线性加权处理，将多目标问题转化为单目标模型;第三，用MATLAB遗传算法求解单目标优化的最优解。

算例分析

某城乡结合部的一个配送中心为3个农村节点和7个城市零售点提供日常消费品和农产品的运输服务，配送中心运用双向运输配送模式。将各节点的需求量和服务时间窗输入系统，通过系统计算得出适合的运输车辆和运输路径，从而保证车辆完成各节点的服务。各节点的地理位置、对产品的需求量和允许的服务时间窗如表1、表2所示，其中城市节点的农产品需求量根据历史数据与经验以一个三角模糊数表示。其他参数设置如下：货车最大载重Qv =3t，货车最大行驶距离Dv=700km，车辆启用固定成本C0=70元，单位车辆单位距离配送成本C1=3元/km，单位时间惩罚成本2=单位时间等待成本1=20元/h，车辆平均行驶速度V1=50km/h，装卸速度V2=30min/t，δ1=0.17，δ2 =0.68，δ3=0.15。

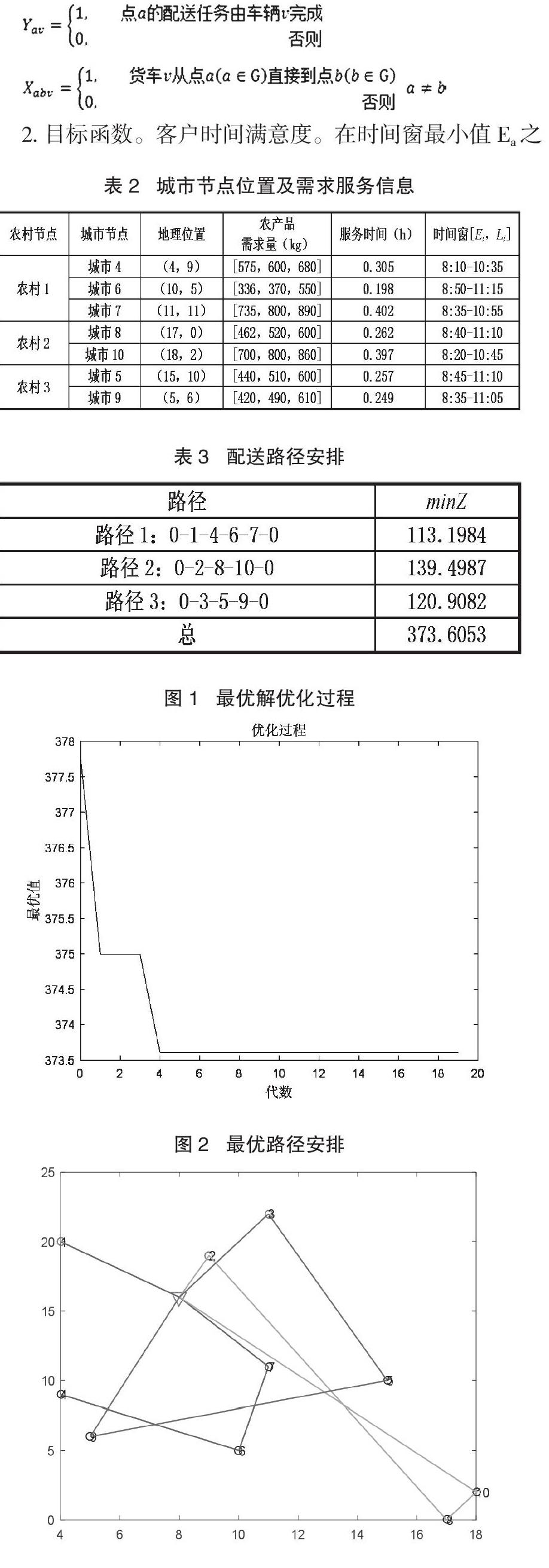
本文使用MATLAB R2016a遗传算法来解决该算例，将初始种群大小设置为10，并且最大迭代次数为20，交叉概率取值为0.9，变异概率取值为0.05，代沟取值为0.9，经过编程多次求解，配送路线有3条，路径1为0-1-6-10-8-4-0，路径2为0-2-4-9-7-0，路径3为0-3-7-5-0，结果如图1、图2所示。

如表3所示，配送路径的最小目标值为373.6053，这一路径各需求点均能够在服务时间内到达，且客户的满意度较高，从而实现了双向路程中的载货提供服务，其仅在城市点服務完毕之后返回配送中心的一段路程中有空载的情况，这提高了车辆的利用率，降低了车辆空载率。

参考文献：

1.王素仙，杨华玲，王力锋.建立城乡双向流通商贸流通体系的战略构想[J].改革与战略，2017，33（11）

2.贺玮，杨克岩.新常态下城乡双向商贸流通体系建设研究[J].商业经济研究，2018（08）

3.秦星红，魏光兴，周靖.城乡统筹双向物流体系构建：以重庆市为例[J].科技管理研究，2011，31（13）

4.彭永涛，李丫丫.基于变分不等式的城镇物流网络优化研究[J].数学的实践与认识，2018，48（09）

5.彭永涛，杜建国，罗建强.基于新型城镇化的城乡配送网络优化研究[J].软科学，2016，30（05）

6.卢美丽.基于城乡物流一体化的连锁经营配送网络优化研究[J].数学的实践与认识，2012，42（22）