基于变分模态分解的相关能量熵自适应阈值去噪
2019-10-28刘霞,李文
刘 霞, 李 文
(东北石油大学 a.电气信息工程学院;b.土木建筑工程学院, 黑龙江 大庆 163318)
0 引 言
在地震勘探中, 主要通过研究地震波在地层中的传播规律, 从而获取地下的岩性分类以及油气藏等信息。而检波器采集到的地震数据中包含的噪声会影响地震资料的反演与解释, 如何有效抑制噪声的影响, 一直是地质勘探领域的研究热点和难点问题之一。地震信号是一种非平稳信号, 由不同传播时间的具有不同振幅和频率的地震子波组成。正是基于地震信号的这一特性, 小波变换[1-3]、曲波变换[4-5]、经验模态分解(EMD: Empirical Mode Decomposition)[6-10]、时频峰值滤波算法[11]、局部均值分解[12]和变分模态分解(VMD: Variational Mode Decomposition)[13-16]等现代信号处理方法可以将地震信号进行频率分解, 通过去除高频分量实现信号去噪的目的。在各类算法中如何区分噪声和有效信号的频率分量是去噪算法的关键。小波变换阈值去噪算法是采用将高频小波系数与阈值进行比较, 由大于阈值的高频小波系数和低频小波系数重构信号。EMD方法能自适应的将信号分解为一组从高频到低频的固有模态分量, 去除高频分量, 重构低频分量可实现对信号去噪, 但可能损失高频中的有效信息[17-20]。杨凯等[17]将EMD方法与小波变换模极大值去噪方法相结合, 较好地抑制了地震信号中的随机噪声。张杏莉等[18]通过计算每个变分模态分量的能量熵, 通过能量熵的最小值确定噪声与信号分量的分界, 将信号分量进行重构进行去噪。陈辉等[19]通过不同频带上分量的梯度值和阈值将各IMF分量分区进行去噪处理。笔者在对地震信号进行VMD分解过程中发现, 各IMF分量中都会不同程度包含噪声的影响, 而高频分量中也会有有效信息。如何去除低频分量中的噪声和有效保留高频分量中的有效信息, 是高分辨率地质勘探中要解决的问题。笔者将VMD算法与相关性和能量熵相结合, 将地震信号通过VMD分解为若干IMF分量, 然后将各IMF分量进行相关处理, 区分出有效信号和噪声的数据点位置, 将去除有效信息的IMF分量分成若干子区间, 分别计算各子区间噪声的能量熵, 选取能量熵最大区间的IMF分量系数作为该分量的噪声方差带入阈值公式计算得到该分量的阈值, 再把经阈值处理后的IMF分量重构得到去噪信号。该方法能有效地保留信号中的高频分量, 从而保留了岩性油气藏的重要信息。
1 VMD去噪原理
1.1 变分模态分解原理
Dragomiretskiy等[20]在2014年提出了变分模态分解算法, 该方法将信号分解为具有一定带宽的K个模态分量(IMF), 每个模态分量的中心频率为ωk。将IMF分量中心频率和带宽的估计问题转化为具有约束的变分问题, 通过引入惩罚因子和Lagrange函数将有约束问题转化为无约束问题, 采用交替乘子算法求最优解, 将信号分解为具有一定带宽的IMF频率分量, 最后将各IMF频率分量进行傅里叶逆变换得到时域信号。可将VMD算法看作是维纳滤波器组的推广, 有效解决了EMD算法中的模态混叠现象。具体方法如下。
1)将信号x(t)分解为K个模态分量uk(t),k=1,2,…,K,uk(t)定义为一组调幅-调频信号
uk(t)=Ak(t)cos(φk(t))
(1)
(2)
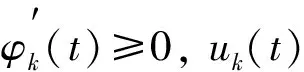
分解的核心问题为找到这K个IMF分量。
2)对每个IMF分量uk(t)进行Hilbert变换, 构造解析信号
3)将每个IMF分量的频谱调制到以ωk为中心频率的频带上,有
(3)
4)在满足式(2)的约束条件下, 按照式(3)信号的梯度平方和(L2范数)最小估算各IMF分量的带宽, 即
5)通过引入惩罚因子α和Lagrange算子λ(t), 将有约束的变分问题转化为无约束的变分问题
6)采用傅里叶变换, 求取二次优化问题的频域解更新公式为
(4)
(5)
(6)
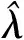
7)对式(4)IMF分量的频域结果进行傅里叶逆变换, 得各IMF分量的时域信号。
1.2 VMD去噪算法
VMD分解算法是将信号分解为具有一定带宽、频率由高到低的K个模态分量, 而信号中随机噪声的频率较高, 主要分布在高频部分, 因此将K个模态分量中的高频部分去除, 将剩余的低频IMF分量重构, 即可得到去噪后的信号
其中l+1,…,K个分量为噪声所引起的。
该去噪算法的关键是找到信号中的有效分量和噪声分量的分界点l。但去除的高频分量中可能包含了部分有用信号, 而保留的低频分量中也可能残留少量的噪声。针对该问题, 笔者提出了基于VMD的相关能量熵阈值去噪算法。
2 基于VMD的相关能量熵阈值去噪算法
2.1 算法思想
地震信号中的高频成分可能包含了岩性油气藏的重要信息, 因此, 在对地震信号进行去噪处理过程中应尽可能的保留这些高频有效信息。在VMD分解中, 地震信号的有效成分主要分布在低频分量中, 噪声主要分布在高频分量中, 但低频分量中也残留一些噪声, 高频分量中也含有有效信息。笔者依据有效信息和噪声对地震信号的相关性不同的特性, 对各IMF分量中的有效信息进行检测与定位, 将有效信息引起的系数剔除, 将噪声引起的系数保留, 得到新的分量系数;这些系数大部分是由噪声引起的, 找到这些系数中噪声影响最大的区域, 只要计算出该区域系数的能量, 再利用噪声的能量构造阈值, 对各原IMF分量系数进行阈值处理, 即可达到去除每个IMF分量中噪声的影响。根据信息熵理论, 系统越有序, 系统的信息熵就越低;系统越混乱, 系统的信息熵就越高。在一个信号中, 噪声是无序的, 因此噪声的信息熵最大, 笔者利用信息熵理论, 将保留的噪声IMF分量系数分成若干子区间, 分别计算各子区间的噪声能量熵, 能量熵最大的区域, 可以认为是全部由噪声引起的, 利用噪声能量熵构造阈值。该方法可根据信号的噪声能量自适应地确定各IMF分量的阈值, 剔除每个IMF分量中噪声的影响。下面给出改进算法的关键计算步骤。
2.2 相关性检测及定位
信号的IMF分量中的有效信息与信号具有较强的相关性, 而噪声与信号的相关性较弱, 根据上述特点, 通过相关处理可突出各IMF分量中的有效信息, 弱化噪声的影响, 实现有效信息的检测及定位。
定义rk(n)为第k个IMF分量uk(n)与x(n)的相关系数
(7)
其中x(n)、uk(n)为信号x(t)和IMF分量uk(t)的离散化表示,n=1,…,N,N为采样点数。
为使相关系数与IMF分量系数具有可比性, 定义规范化相关系数Rk(n)为
(8)
通过各IMF分量的规范化相关系数与各IMF分量系数的比较, 得到有效信号的IMF分量系数位置。
2.3 噪声能量熵计算
根据信号在时频域具有能量守恒特性, 定义第k个IMF分量的能量
将uk(n)分成l等份, 每个小区间的能量记为Eki, 采样点数为N/l, 则有
第k个IMF分量中第i个子区间的能量Eki在该分量的总能量Ek中的概率为
pki=Eki/Ek
则第i个子区间对应的能量熵为
Ski=-pkilnpki
(9)
得到第k个IMF分量的能量熵序列
Sk={Sk1,…,Skl}
2.4 阈值计算
搜索第k个IMF分量的熵值最大子区间, 记为
Skm=max{Sk1,…,Skl}
求第k个IMF分量第m个子区间的IMF分量系数的平均值
定义第k个IMF分量的阈值Tk为
(10)
其中σk为第k个IMF分量的熵值最大子区间的系数的平均值做为噪声方差。该阈值的确定方法可根据信号中噪声的能量特征自适应地确定各IMF分量的阈值。
2.5 笔者方法实现步骤
Step1 对信号进行VMD分解, 得到各IMF分量。

2)n=n+1;
3)按照式(4)k从1~K迭代更新uk;
4)按照式(5)k从1~K迭代更新ωk;
5)按照式(6)计算λ;
6)重复步骤2)~5), 直到满足停止条件
(11)
其中ε为分解精度,ε>0;
7)对K个IMF分量进行傅里叶逆变换得到IMF分量的时域分解信号。
Step2 相关检测及定位:按照式(7)计算各IMF分量与信号的相关系数, 按照式(8)计算规范化相关系数, 将规范化相关系数大于各IMF分量系数的位置记录下来, 这些位置对应了各IMF分量中的有效信号。
Step3 计算噪声方差:把Step2中确定出的含有有效信号的位置处对应的IMF分量系数置0, 得到新的系数, 这些新的系数的采样点数保持不变;将得到的新的系数分成l等份, 分别计算各区间的能量熵, 并进行比较, 选取能量熵最大的区间系数, 认为该区间系数是由噪声引起的, 计算该区间系数的平均值σk, 作为第k个IMF分量的噪声方差。
Step4 计算阈值, 按照式(10)计算第k个IMF分量的阈值Tk。
Step5 根据得到的阈值Tk, 利用软阈值函数分别对各IMF分量系数进行阈值处理, 得到新的IMF分量系数。
Step6 重构:利用新的IMF分量系数重构信号, 得到去噪后的信号。
3 数值仿真
3.1 Ricker子波模拟地震信号仿真
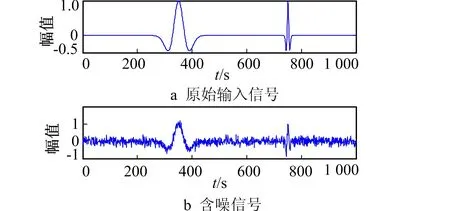
图1 Ricker子波及加噪信号
我国很多陆相油气田都属于薄储层油气藏, 为模拟薄储层油气藏, 构造由2个Ricker子波合成的加噪信号, 分析笔者改进VMD去噪算法的性能, 并与直接去除高频分量VMD去噪方法进行对比。Ricker子波及加噪信号(信噪比为2 dB)如图1所示, 对加噪信号进行3层VMD分解的IMF分量如图2所示, 2种方法的去噪效果对比如图3所示。不同噪声水平下的2种方法信噪比(SNR: Signal to Noise Ratio)和均方根误差(RMSE: Root Mean Squared Error)对比如表1所示。
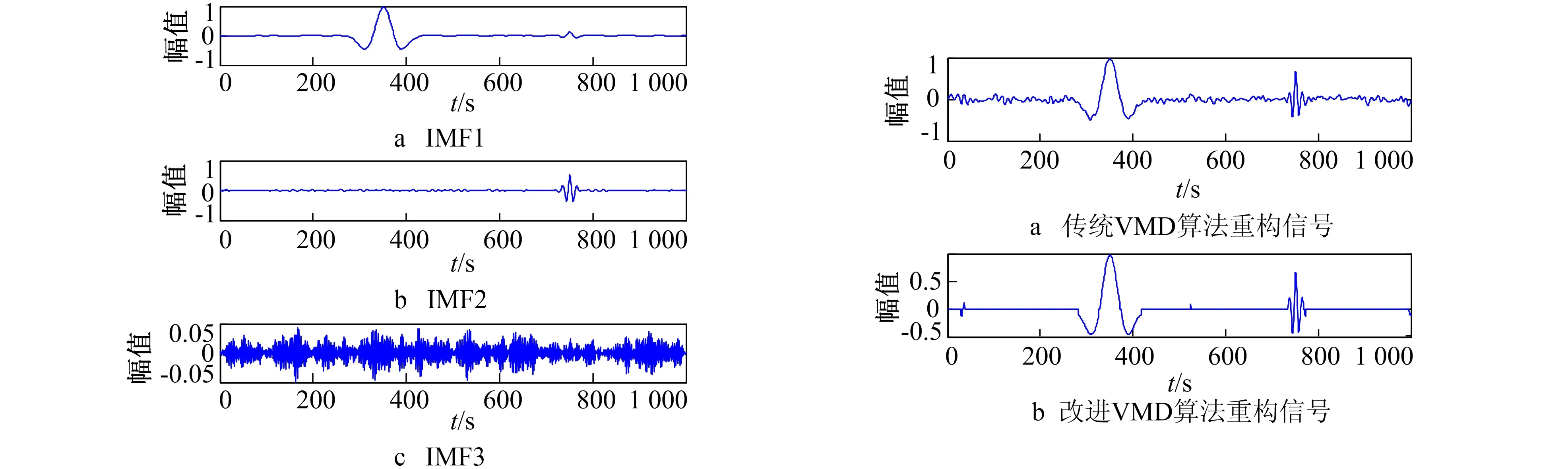
图2 Ricker子波3层VMD分解 图3 去噪效果对比

表1 不同噪声水平下的去噪效果对比
从图1原信号和加噪信号的波形可以看出, 第2个Ricker子波分量已大部分淹没在噪声中, 从图2的VMD3层分解的IMF分量中可以看出, 原信号的2个Ricker子波分量和噪声较好的分离出来, IMF3分量噪声含量较高, 但前2个IMF分量中也都有噪声的影响。采用笔者VMD改进算法, 对每层IMF分量都进行阈值处理, 从图3的2种方法的去噪效果可以看出, 笔者算法重构效果优于直接去除高频分量的VMD去噪效果, 去除了大部分噪声, 较好地保留了2个Ricker子波的形状;表1中给出了对不同信噪比的信号进行去噪处理的信噪比和均方误差, 可以看出, 笔者方法在2个指标上都优于直接去除高频分量的VMD去噪效果, 在低信噪比较低时, 具有更好的去噪效果。
3.2 合成地震信号去噪效果对比
由一个低频Ricker子波和一个高频Ricker子波叠加构造薄储层楔形地震模型, 如图4所示。反射层的上层速度为2 000 m/s, 下层速度为3 000 m/s, 深度为100 m, 最小偏移距离10 m, 记录时间长度512 ms, 密度1, 采集道数30。对图4模型加上信噪比为2 dB的高斯白噪声, 构造含噪地震模型如图5所示。
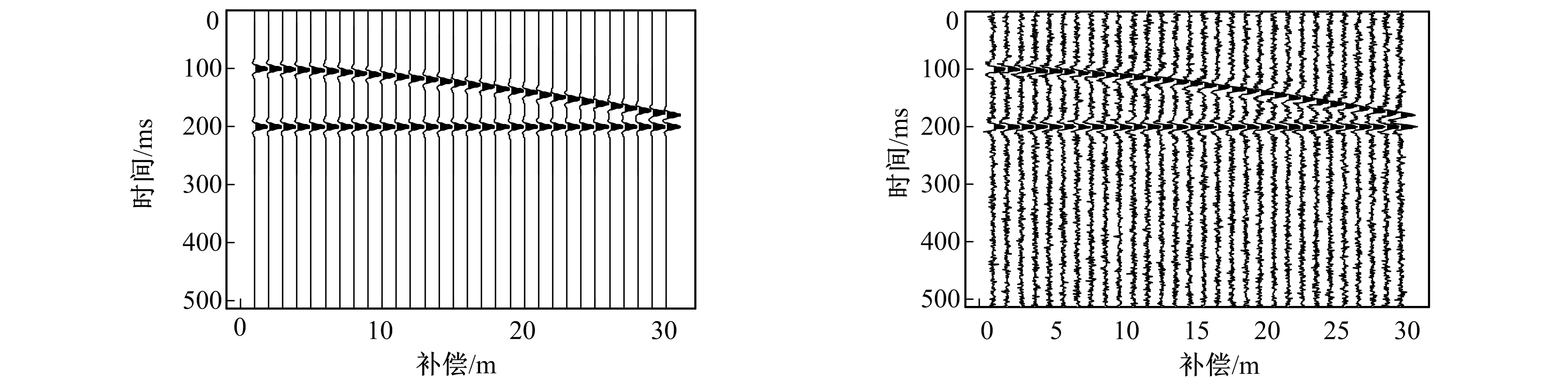
图4 地震信号剖面图 图5 含噪地震信号剖面图
通过图6采用直接去除高频分量的VMD方法去噪效果中可以看出, 地震剖面中还残留了部分噪声, 去噪后信噪比为2.92 dB。从图7中可以看出, 笔者方法很好的抑制了噪声, 同相轴保留完整, 分辨率更好, 有效信号得到更好的保护, 去噪后信噪比为6.25 dB, 去噪效果更好。

图6 传统VMD去噪后的地震剖面 图7 笔者方法去噪后的地震剖面
4 实际地震信号去噪
从某地区实际地震资料中选取100道信号, 每道采样点为1 024, 采样间隔为2 ms, 地震剖面如图8所示。采用直接去除高频分量的VMD方法和笔者方法进行去噪处理, 去噪剖面图如图9、图10所示。

图8 实际地震剖面图 图9 VMD方法去噪后地震剖面 图10 笔者方法去噪后
从图8的实际地震信号中可以看出, 剖面图中含有大量的噪声, 同相轴不清晰。通过图9和图10可以看到, 两种方法都抑制了噪声的影响。但直接去除高频分量的VMD方法削弱了同相轴, 使有效信息损失较大, 而笔者方法去噪后的地震剖面同相轴连续、清晰, 很好的保留了有效信息。
5 结 语
笔者针对直接去除高频分量的VMD去噪方法中, 不能有效区分各IMF分量中的有效信息和噪声问题, 提出了基于变分模态分解的相关能量熵自适应阈值去噪方法, 该方法通过相关处理检测有效信息并定位, 根据噪声的能量熵自适应地确定各IMF分量的阈值。通过对不同噪声水平下的地震模型测试和实际地震信号去噪处理表明, 笔者方法能更有效的从强噪声背景下提取有效信息, 去除混叠噪声的影响, 提高信噪比, 为地震资料的解释等工作提供高分辨率地震数据。
