一种新的球载雷达气象杂波抑制方法
2019-10-28张小涵刘润华汪枫宿文涛
张小涵,刘润华,汪枫,宿文涛
(空军预警学院,湖北 武汉 430019)
0 引言
近年来,球载雷达以预警能力强、生存能力强、留空时间长和效费比高等优势,越来越受到世界各国军队的青睐[1-4]。由于球载雷达探测平台的升高,导致雷达波束会直接照射地面,另外球载雷达平台的移动会使地杂波频谱展宽,所以球载雷达工作时面临着很强的地海杂波和气象杂波,增加了探测低空小目标的难度[5]。
低速目标经常处于低空甚至超低空飞行,受到强大的地海杂波和气象杂波的干扰,且低速目标速度较慢,其在多普勒域与杂波存在严重的交叠,难以通过传统的频域滤波方法抑制杂波。目前军事中应用的无人机属于低速飞行器[6]。目前运动平台下的慢速目标检测常采用偏置相位中心天线(displaced phase center antenna,DPCA)[7-9]和空时自适应处理技术(space time adapteve processing,STAP)[10-12],但这些方法要求雷达为相控阵体制或者具有数字波束形成能力,因此均难以直接应用于现有的球载雷达装备。但是传统的动目标显示(moving target indication,MTI)技术或动目标检测(moving target detection,MTD)技术在滤去杂波的同时也会滤去混叠在杂波谱中的低速目标信号,从而导致漏警。针对上述问题,本文从回波建模出发,使用Kalmus滤波器抑制气象杂波,保留目标信息,通过计算机仿真,验证了方法的有效性,并分析了算法的性能和适用条件。
1 球载雷达回波模型
为了建模方便,将雷达放置于北天东坐标系中,并假设云层等气象环境类似于均匀的地面,球载雷达气球只做水平匀速运动,速度为v,目标相对于雷达以速度v做匀速运动,空间模型如图1所示。
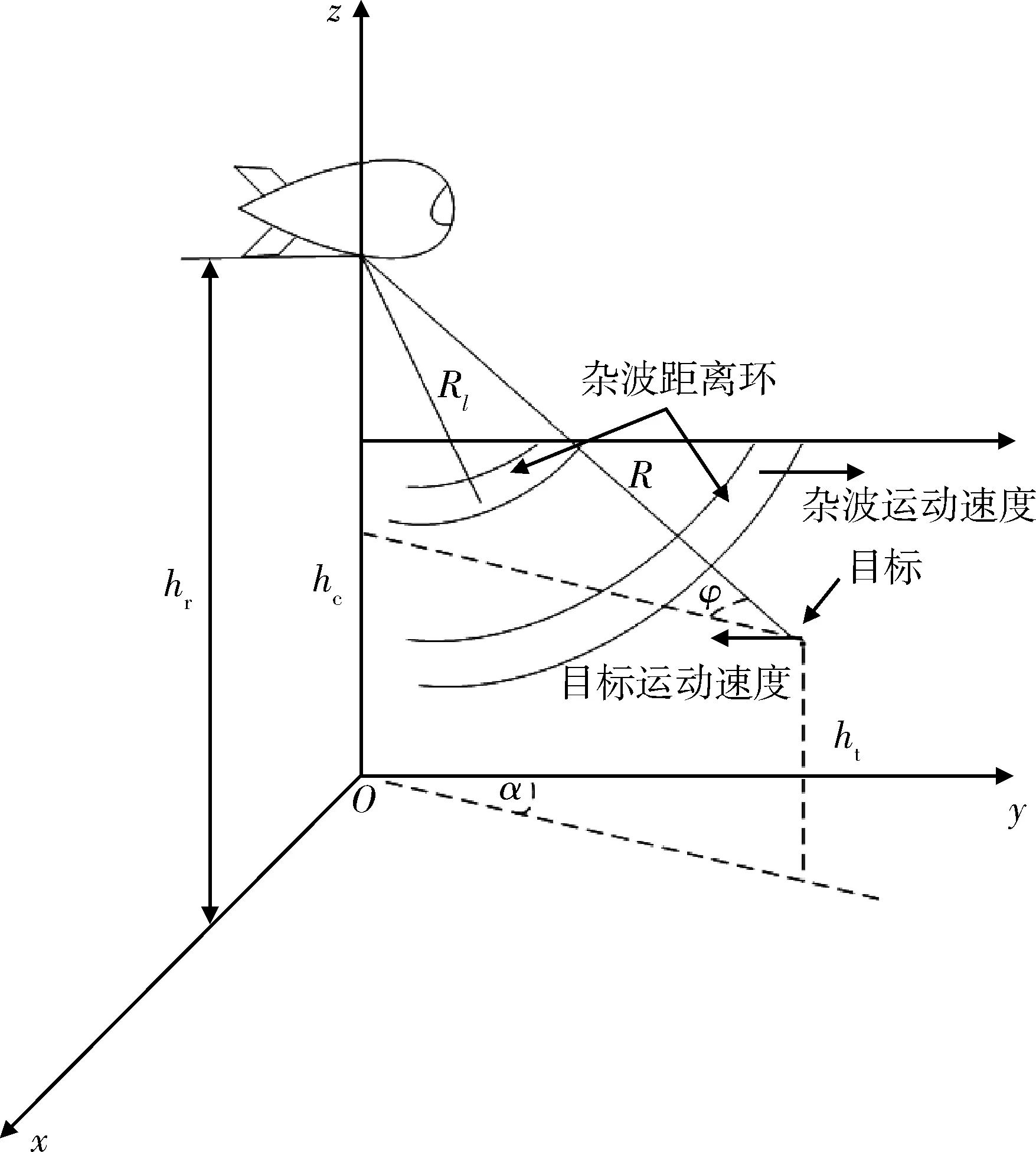
图1 空间模型Fig.1 Space model
图1中ht表示目标的高度,α为目标的方位角,φ为目标的俯仰角,目标与雷达的距离为R,hr表示雷达的高度,hc表示云层的高度。
1.1 无人机目标模型
本文中的无人机目标属于中小型无人机,其航程较近、飞行速度和高度较低,它的雷达反射截面积(RCS)据估算一般为0.2 m2。为了简化模型,本文将无人机目标简化为一个RCS为0.2 m2的点目标。
根据图1中几何关系,目标相对于雷达的距离变化模型可以表示为
R(tm)=R-vtmcosφcosα
.
(1)
由于球载雷达工作于中重频时,存在距离模糊,因此目标到雷达的视在距离修正为
R′=R-kRu,
(2)

则目标的回波为
(3)
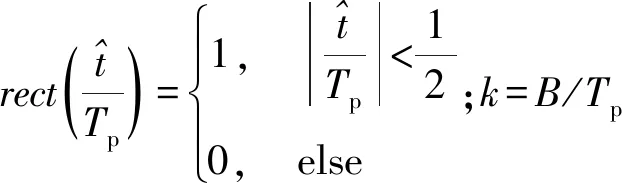
1.2 气象杂波模型
雷达接收到的云、雨和雪的散射回波称为气象杂波。气象杂波是一种体杂波,其强度与天线波束照射的体积、信号的距离分辨率以及散射体的性质有关[13]。
如图1所示,气象杂波信号由来自多个等距离圆弧的杂波信号叠加组成。这些等距离圆弧可以叫做杂波距离环,杂波距离环数的计算公式如下:
(4)
式中:int()为取整函数;Rmax为雷达最大作用距离。
第l个距离环第i个分辨单元的杂波功率,由雷达方程有
(5)
Rl=(hr-hc)+l·Ru,
(6)
式中:Pt为雷达发射功率;G为雷达天线增益;λ为发射波长;σc为杂波截面积;Rl为第l个距离环上杂波分辨单元到雷达的距离。
杂波截面积σc计算公式为
σc=ηVc,
(7)
(8)
(9)
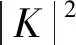

表1 几种情况下降雨率γ的典型值Table 1 Typical rainfall rate (mm·h-1)
由于气象杂波多普勒频率较小,而球载雷达脉冲重复频率为几千赫兹,所以一般不存在多普勒模糊。模拟气象杂波时,将一定范围内的云层划分为网格状,一个网格表示一个杂波分辨单元。先计算一个网格即一个分辨体积单元中的杂波回波,再将同一个距离环上的所有网格的杂波信号相加,得到一个距离环的杂波回波,求得各个距离环上的杂波回波后,将各个距离环上的杂波回波相加即可得到落入一个距离门的杂波。根据杂波距离环宽度计算在球载雷达最大不模糊距离内距离门的个数,将落入每个距离门的杂波信号叠加起来,即可得到整个观测范围内的球载雷达气象杂波。
根据上述方法可求得第l个距离环第i个分辨单元的杂波信号为
Cil(k)=PilAilexp[j2πfd(k-1)Tr],
(10)
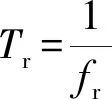
第l个距离环的杂波信号为
(11)
式中:n为距离环内分辨单元个数。
某个距离门的杂波信号为
(12)
式中:L为杂波距离环个数。
经过多年的研究,气象杂波的幅度值为瑞利分布,功率谱一般被看作高斯谱[15]。气象杂波功率谱的表达式为
(13)
式中:σf为杂波谱的标准差,代表频谱展宽的程度。
考虑到气象杂波单元有一定的运动速度v,杂波功率谱修正为
(14)

2 无人机目标检测方法
为实现无人机目标的有效检测,首先要考虑气象杂波的抑制,即将目标多普勒频率附近的杂波谱能量抑制掉。这种滤波器应该在气象杂波多普勒频移附近呈现深的止带凹口,并随着频率的增加快速增大,以保证无人机目标的检测能力。对于FIR数字滤波器,要形成这种滤波器需要很高的阶数,而Kalmus滤波器则具备这一特点。
2.1 Kalmus滤波器的设计
2.1.1 云雨杂波速度估计
云雨杂波的复包络为
sc(t)=Aej(2πfdt+φ0)=Aej(ωdt+φ0),
(15)
式中:φ0为初始相位;A为回波幅度。
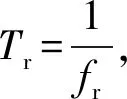
Sc1=A1ejψ1=A1ej(ωdt+φ0),
(16)
Sc2=A2ejψ2=A2ej(ωd(t-Tr)+φ0).
(17)
由式(16),(17)可得2回波的相位差为
Δψ=ωdTr=2πfdTr.
(18)
(19)
球载雷达采用正交双通道处理信号,因此相邻周期杂波回波的相位差可由下式求得
(20)
式中:I1,I2和Q1,Q2分别为2个周期杂波信号的同相分量和正交分量。
将式(20)带入式(19)中,即可得到根据杂波回波估计出的杂波径向速度vc。
2.1.2 Kalmus滤波器幅频响应
Kalmus滤波器可以通过2个具有共轭关系的滤波器来实现,其传输函数为
|HKalmus(f)|=|H(f)|-|H*(f)|,
(21)
式中:|H(f)|可以通过离散傅里叶变换DFT等效的梳状滤波器来实现。
通过离散傅里叶变换DFT的定义能够推导出DFT等效为一个滤波器组,其响应函数为
(22)
式中:n=0,1,…,N-1,N是滤波器的阶数,0≤k≤N-1是滤波器的组号。
Kalmus滤波器示意图如图2所示。
球载雷达脉冲重复频率为fr,滤波器个数为m,将各滤波器平移fr/2m,再将滤波器1和2的幅频特性相减并取绝对值,就可以形成有窄深凹口的Kalmus滤波器。通过上述分析,求得的DFT等效
滤波器情况下Kalmus滤波器的幅频响应为
(23)
由于云雨杂波有一定多普勒频移fd,因此为了取得好的滤波效果,Kalmus滤波器也需要作相应的频移,Kalmus滤波器的幅频响应修正为
(24)
Kalmus滤波器的幅频响应如图3所示。
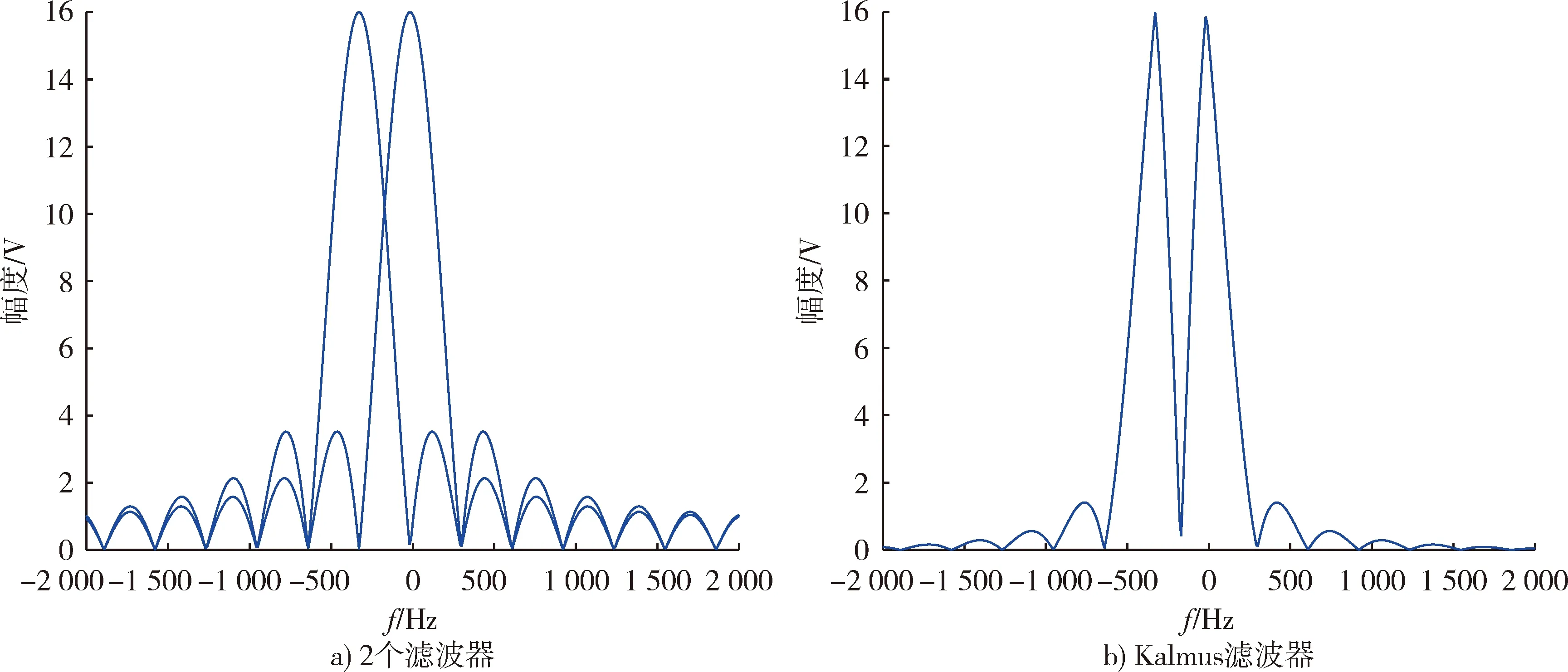
图3 滤波器幅频响应Fig.3 Amplitude-frequency response
由图3a)可以看出,2个滤波器的幅频响应修正后关于气象杂波多普勒频移对称,将它们幅频响应相减后再求绝对值即可得到图3b)。由图3b)可看出经过修正的Kalmus滤波器在气象杂波多普勒频移处呈现深的止带凹口,这个凹口提供了抑制气象杂波的能力。Kalmus滤波器随着频率增加呈现快速上升斜率,使它尽可能地保留了低频分量,从而改善了低速目标的信杂比。Kalmus滤波器这种特性正是检测低速目标所必须的。由Kalmus滤波器的幅频特性可知,它只能保留特定频率范围的信号。当目标速度与云层速度很接近时,或者当目标多普勒频率不在Kalmus滤波器所能保留的范围中时,目标回波分量也会被Kalmus滤波器滤除,此时这种气象杂波抑制方法是失效的。
2.2 检测流程
图4给出了基于Kalmus滤波器的目标检测流程,主要包括2部分:一是气象杂波抑制;二是对滤波后剩余的回波进行目标检测。具体流程如下:首先对雷达接收到的回波使用Kalmus滤波器进行滤波,在使用恒虚警技术进行目标检测,以达到检测出被杂波淹没的无人机目标的目的。
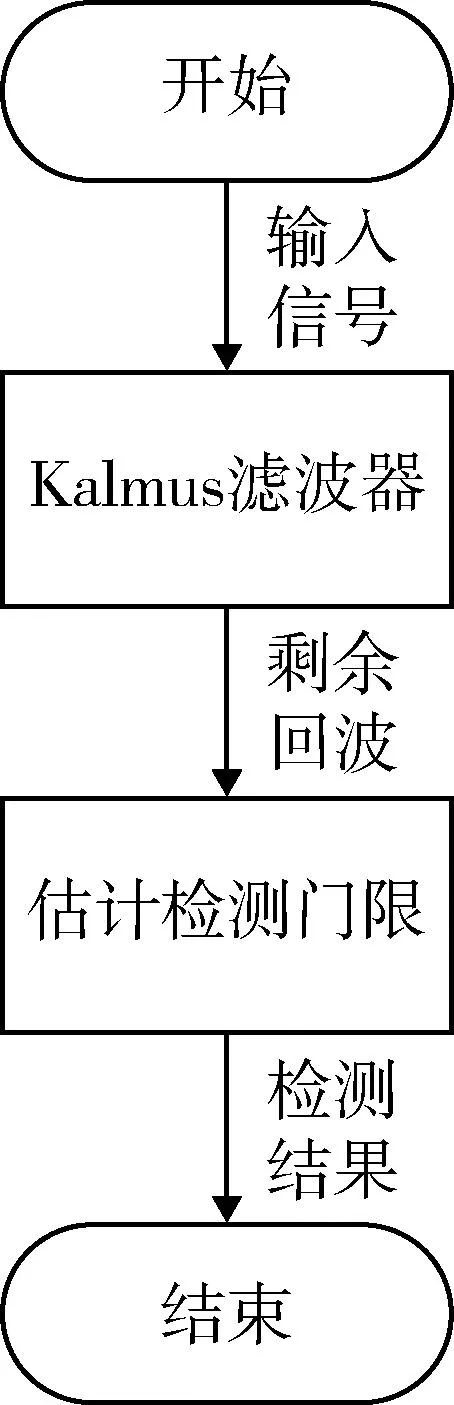
图4 检测流程Fig.4 Detection flow
3 仿真校验
目前球载雷达有2种常用的工作模式,在对地模式下使用AMTI模式对消杂波,在对空工作模式下使用PD模式检测目标。为了验证本文提出的基于Kalmus滤波器的目标检测的性能,设置相应的仿真参数,将对空模式下抑制杂波的方法与本文提出的方法进行了对比。
仿真参数设置如下:
雷达高度hr=2 000 m;脉冲重复频率PRF=4 000 Hz;雷达最大天线增益Gt=32 dB;发射功率Pt=15 kW;天线俯仰波束宽度θB=8°;天线水平波束宽度φB=2°;载频f0=3.2 GHz;调制带宽B=4 MHz;波长λ=c/f0=0.094 m;脉冲宽度τ=25 μs;最小探测距离Rmin=3.75 km;最大探测距离Rmax=200 km;云层高度Hc=1 km,运动速度v=20 m/s;相干处理脉冲长度K=32;目标高度ht=700 m;目标到雷达的初始距离R=155 km;目标初始方位角α=40°;目标初始俯仰角φ=arcsin[(Hr-Ht)/R]=0.90°,目标雷达截面积σ=0.1 m2,目标速度v=35 m/s,杂波起伏模型为瑞利分布,Kalmus滤波器的阶数N=16。
3.1 抑制杂波效果对比
对同一个距离单元上的回波对K个脉冲作FFT,得到此距离单元的回波多普勒谱,对所有距离单元作FFT,则得到球载雷达接收到的回波距离—多普勒谱,图5给出了降雨率γ=16 mm/h和γ=40 mm/h 2种情况下,上述杂波抑制方法的回波距离—多普勒谱。
根据给出的脉冲重复频率,得出最大不模糊距离为37.5 km。图5可以看到由于存在距离模糊,本应分布在整个接收距离的回波都只在37.5 km内混叠,且越靠近雷达幅度越强。由图5a)可以看出,目标和气象杂波的多普勒速度非常接近,且气象杂波比目标回波强许多。由图5b)可知,经过Kalmus滤波器后,气象杂波的幅度有了明显的下降,目标回波信号高出气象杂波,说明Kalmus滤波器有效地改善了信杂比,为下一步检测提供了条件。图5c)可以看出随着杂波强度的增强,目标回波已经完全被淹没在杂波中。由图5d)可以看出经过Kalmus滤波器后,气象杂波的幅度有所下降,但目标回波没有高于杂波,信杂比没有明显改善。通过对比不同强度杂波滤波结果说明,Kalmus滤波器在杂波强度很大的时候是失效的,滤波器对信杂比的改善是有限的。
3.2 检测结果对比
对经过上述杂波抑制处理后的剩余波形进行二维恒虚警检测的结果,如图6所示。

图5 各种方法滤波结果Fig.5 Clutter suppression results
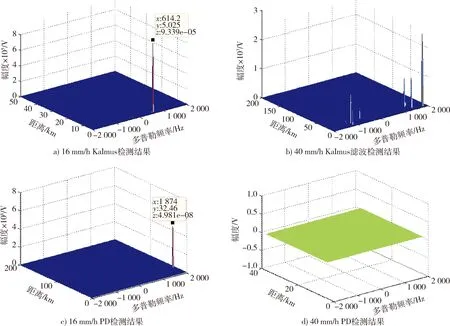
图6 恒虚警检测结果Fig.6 CFAR results
图6中的检测结果均是将滤波后的剩余回波与计算出的门限相减小于0的部分置0以后的结果。由图6a)可知,由于距离模糊,检测出的目标位于5 km处,且多普勒频率为641.2 Hz,与理论值571.4 Hz基本相符,说明目标回波经过PD处理后再进行Kalmus滤波说有效的。图6b)可知,当杂波很强时,Kalmus滤波方法失效,对信杂比改善有限,无法检测出目标。由图6c)可知,目标的距离与多普勒频率与理论值不符,是一个虚警,没有检测到真实目标。图6d)中没有目标过门限,也没有检测到真实目标。图6c),6d)说明,仅使用PD处理技术,无法达到抑制气象杂波检测出慢速目标的目的,这是由于目标和杂波多普勒速度接近,无法使用多普勒信息对杂波和目标进行区分,造成了目标丢失。由图6a),6c)可知,回波经过Kalmus滤波器处理,低速目标的检测性能得到了一定改善,避免了与气象杂波多普勒频移太过接近而导致的目标丢失。
3.3 改善因子
改善因子的定义是输出信号杂波功率比(So/Co)和输入信号杂波功率比(Si/Ci)的比值,是评判杂波抑制方法性能的一个重要指标。改善因子可以表示为
(25)
根据仿真参数,在降雨率为16 mm/h的情况下,只进行PD处理的改善因子通过计算为22.22 dB,PD处理后经过Kalmus滤波器的改善因子为33.32 dB,相比只经过PD处理增加了9.9 dB。因此,在一定的气象条件下,Kalmus滤波器可以较好地改善信杂比。
4 结束语
本文对球载雷达目标和气象杂波进行了建模与仿真,并针对无人机目标和气象杂波多普勒速度接近难以检测的问题提出了解决方法。通过仿真分析,在相应的条件下,该方法对信杂比有很好的改善效果,使目标容易被检测。由于不必考虑回波的相位信息,其实现过程比相干处理更加简单,降低了系统设计的复杂性;另外,不同于传统的运动平台下的慢速目标检测方法,Kalmus滤波方法可以直接应用于目前现有的球载雷达装备。综上所述,Kalmus滤波方法完全可以作为球载雷达抑制气象杂波检测无人机目标的一种有效方法。
