基于EXCEL的设备振动频谱分析系统
2019-10-26薛亚芳乔文生艾士娟
薛亚芳,乔文生,艾士娟,刘 欣
(1.中北大学仪器与电子学院,山西太原 030051;2.北京航天拓扑高科技有限责任公司,北京 100176)
0 引言
振动频谱分析软件是设备诊断常用的重要工具之一,在工作中首选仪器制造厂商研制的专业软件。但作为振动分析的从业人员应了解频谱分析软件的基本原理,甚至自己动手编写一个简单的频谱分析软件。利用Matlab,VB,VC,C#,LabView 等专业编程软件可以实现。利用Microsoft Office 2016 中的ECXEL软件,实现以北京航天拓扑公司生产的HG8900 数据采集故障诊断系统检测的振动数据为对象,进行频谱分析的方法。HG8900 数据采集故障诊断系统的数据文件以Tab 为分隔符,以文本文件形式保存,便于用户进行二次开发。
1 标准正弦信号的生成与分析
在信号分析中,常常以简谐信号分析入手,判断分析系统的准确性,再分析其他复杂信号,因此分析系统应首先实现标准正弦(余弦)信号的生成与分析,并关注频谱分析过程中应注意的技术细节。
假设有一信号为:y=a0+a1sin(2πf1t+φ1)+a2sin(2πf2t+φ2)。式中a0为直流量;a1,a2分别为两正弦信号的幅度;f1,f2为频率;φ1,φ2为初相角。这7 个参数在分析系统中为手动输入量,可以调整,便于检验分析系统的准确性。
频谱分析中一定要注意“零均值”处理,即首先求取信号序列的算术平均值,然后再用原始信号中的每个数值减去算术平均值,这样处理后的信号在做频谱分析时不会在0 Hz 处存在明显的频率分量,国内外部分频谱分析仪的0 Hz 分量明显就是这个原因。
利用EXCEL 软件实现标准正弦信号的生成与频谱分析功能主要分5 个步骤:
(1)启动EXCEL 软件,将“Sheet1”改名为“标准波形生成与分析”,在“A”列的1 行到10 行分别填入“参数名称”,在“B”列分别填入参数值,见图1。
(2)“C”列第2 行开始填入公式“=$B$4*SIN(2*PI()*$B$5*(ROW($C2)-2)/(2.56*$B$2)+$B$6*PI()/180)+$B$7*SIN(2*PI()*$B$8*(ROW($C2)-2)/(2.56*$B$2)+$B$9*PI()/180)+$B$10”用于存储原始波形数据,这里的sin 函数变量按弧度计算,因此要将常用度数变换为弧度。在“D2”单元格写入公式“=AVERAGE(C2:C1025)”用于存放原始波形数据的算术平均值。“E”列填入公式“=C2-$D$2”用于存放“零均值处理”后的波形数据。见图2。
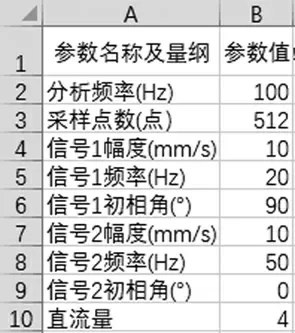
图1 参数名称及参数值

图2 零均值处理
(3)如果“数据”菜单中没有“数据分析”子项,则在“开发工具”菜单中选择“Excel 加载项”,勾选“分析工具库”及“分析工具库-VBA”。如果“数据”菜单中已经有“数据分析”子菜单则可从其“分析工具”中选择“傅利叶分析”对“E2:E1025”进行分析,生成的数据存入“G2:G1025”。傅利叶分析得到的是复数序列,对“G2:G1025”求模存入“H”列,即在在“H2:H1025”输入公式“=IMABS(G2)/512”。至此就得到了频谱分析的幅值谱数值,篇幅所限这里不予讨论相位谱分析编写过程。另为了对比有无“零均值处理”在频谱分析中的影响,同样对原始波形信号进行傅利叶分析并求模。分别存于“I”列和“J”列。如图3 所示。

图3 频率值、傅利叶变换及求模
(4)根据分析频率、采样点数(谱线数)等信息,计算各频率分量的频率值。即在“F2:F402”填入公式“=$B $2* (ROW($F3)-2)/$B$3*2.56”,该列数值可以作为频谱图的横坐标。
(5)对原始波形数据、零均值处理后的波形数据添加图表进行分析,横坐标为数据点数,纵坐标为波形数据值。对原始波形的频谱、零均值处理后的频谱分别添加图表进行分析,横坐标为“F”列频率值,纵坐标为“J”列和“H”列的计算值。需要注意的是,频谱数据只需要取前一半谱线分析即可。按照采样定理,可以分析的最高频率f1为采样频率fs的一半,即f1=fs/2。为了保证信号的准确性,工程上一般选择f1=fs/2.56。例如1024 点的数据进行傅利叶变换可得到1024 条谱线,但是数学计算上存在负频率,前512 条谱线与后512 条谱线是对称的,实际上关注的是正频率部分对应的谱线,也就是说正频率有512 线,通常情况下由于频率混叠和时域截断的影响,一般认为401 线到512 线的频谱精度不高而不予考虑,故仅分析前400 条谱线。即当采样频率为2560 Hz 时,理论上最高可分析到1280 Hz 的信号,但实际上仅分析2560/2.56=1000 Hz 以内的信号。原始波形和零均值处理后波形对比见图4。
如图5 所示,原始波形幅值谱在0 Hz 处存在直流分量,经零均值处理后的幅值谱则没有。至此,基于EXCEL 的标准正弦信号的生成与频谱分析功能已经实现。
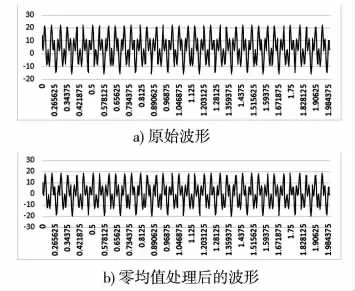
图4 原始波形与零均值处理后的波形对比

图5 原始波形频谱与零均值处理后波形频谱对比
2 文本型数据的读入与分析功能
在上述功能的实现中采用了“列”的方式存储数据,本节设计中尝试用“行”存储数据。首先增加“Sheet2”并更名为“读数据文件”。为了便于将波形及频谱图集中显示于上部,将数据存放于26 行。“A”列及“B”列前几行依然存放参数名称及参数值。从“数据”菜单中选择“获取外部数据”中的“自文本”按步骤导入文本数据文件。将公式“=COUNT($26:$26)”填入“B4”单元格,自动读取采样点数;采样频率填入“B3”,分析频率填入“B2”,计算公式为“=B3/2.56”。
选择“开发工具”中的“插入”,再选择“表单控件”中的按钮控件,在表单上增加一按钮,命名为“分析”,录制或修改宏命令,并将宏命令与“分析”命令按钮关联。宏命令的主要目的是针对不同数据文件采用点数、采样频率可能不同,要根据不同采样点数计算各频率分量的频率值,以及自动设置傅利叶分析的数据范围。
部分宏指令为:

点选某文本型数据文件,读入到数据存放行,进行分析则实现如图6 所示分析功能。

图6 文本型数据文件频谱分析功能
3 结束语
通过以上各步骤的实施,实现了标准正弦信号的生成与分析,验证了频谱分析功能的准确性;实现了利用EXCEL 针对HG8900 数据采集故障诊断系统的文本型振动数据的频谱分析。通过对比分析明确了“零均值处理”在频谱分析中的作用,同时也拓展了办公软件的专业分析功能,如进一步挖掘,将可以实现许多个性化的分析功能。
