等截面裂缝梁自由振动分析的正问题

王敏杨，刘文会*，朱志清，刘 洋，郑嘉俊

1吉林建筑大学 交通科学与工程学院，长春 130118 2吉林大学 交通学院，长春 130022

0 引言

裂缝是结构最常见的损伤之一,裂缝的存在将极大地影响结构的性能和剩余寿命.结构在使用过程中经常受到动荷载作用,因此,裂缝结构的动力特性引起了人们的广泛关注.另一方面,裂缝的存在会引起结构物理参数的变化,从而引起结构动力特性的变化,因此,基于动态特性的损伤识别具有很大的潜力[1].

在我国,因简支梁为数众多,且应用广泛,故研究含等截面裂缝梁进行自由振动分析的正问题具有重要意义.裂缝梁的动力特性研究受到了广泛的关注,并采用各种解析、半解析和数值方法求解了裂缝梁结构的振动分析问题.利用修进的Fourier级数(Modified Fourier series,英文缩写为MFS),Zheng等[2]人得到了具有任意数目横向开裂缝的非等截面梁的固有频率,提出了一种计算任意数量横向开裂纹非均匀梁固有频率的简便新方法.Banerjee[3]应用Witticy-Williams算法求解了梁的固有频率和振型,给出了悬臂梁在端处承载弹簧质量系数的数值例子，然后通过改变弹簧质量系统的质量和刚度特性进行了参数化研究，并说明其对固有频率和振型的影响.Huang等[4]人为了求解振型和频率,将传统的4阶控制微分方程转化为Fredholm积分方程,提出了一种新的、简单的求解可变弯曲刚度和质量密度的梁自由振动固有频率的方法.Koplow等[5]人得到了横截面阶跃变化的Euler-Bernoulli梁动力响应解析解,考虑自由边界条件的情况，提出了由简谐力或两端耦合激励引起的直接频率响应函数.Firouz-Abadi等[6]人利用轴向变截面Euler-Bernoulli梁运动控制方程及自振频率得到奇异微分方程,并采用WKB展开级数求解，并在此基础上，给出了确定固有振型形状及相应频率的封闭形式解.

有限元法(Finite element method,英文缩写为FEM)在损伤梁的自由振动分析中得到了广泛应用,而有限元法的关键问题是如何恰当地求出裂缝梁单元的刚度矩阵.结构损伤识别在保证安全、实施救援和避免紧急行动等方面发挥了重要作用.本文提出了一种分析方法来研究等截面裂缝梁的自由振动分析.

1 等截面裂缝梁式结构动力特性正问题求解方法

如图1所示的典型等截面裂缝梁式结构中,位于x轴下方的1,2,…,j,…,N表示裂缝编号;j为梁跨的第j条裂缝;L表示等截面梁两支撑间的距离;xj表示第j条裂缝距左端支撑的距离.

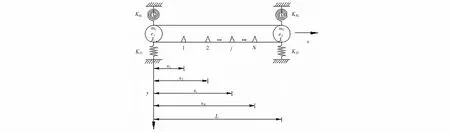
图1 等截面梁裂缝梁式结构Fig.1 Beam structure with equal section cracks in simply supported beams

由截面Euler-Bernoulli梁的自由振动方程,可得等截面梁振型函数φ(x)：

(1)

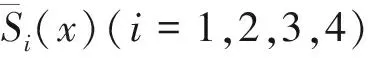
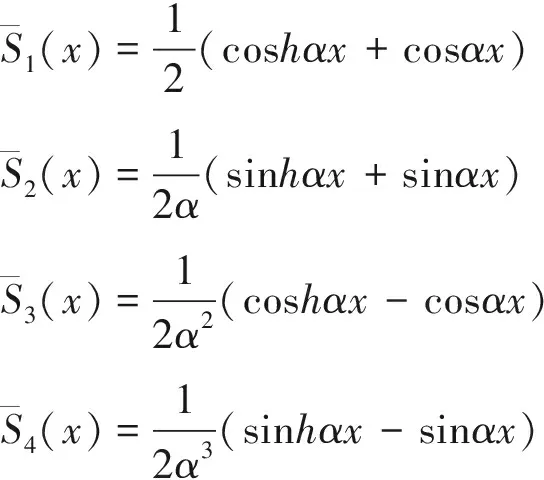
(2)

采用φ(0),φ′(0),M(0),Q(0)表示梁跨左端(x=0)处的位移、转角、弯矩和剪力,本文称之为梁跨的4个初始参数.综合式(1)、式(2)的整理过程,可得梁跨第1个梁段的振型函数：

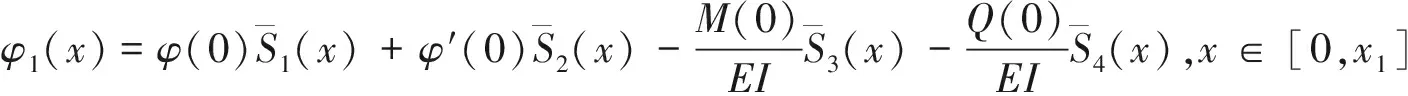
(3)

采用无质量扭转弹簧模拟裂缝，可以认为裂缝两侧的位移、弯矩、剪力相等，转角存在突变.对于图1中的第j条裂缝，相邻两梁段裂缝左右两侧且无限趋近于裂缝处的位移、位移二阶导数以及位移三阶导数均相等，并且有：

φj+1′(xj+)-φj′(xj-)=Cjφj″(xj-)

(4)

式中,xj-代表从左侧无限趋近于xj；xj+代表从右侧无限趋近于xj；Cj为梁跨第j条裂缝处的局部柔度系数；φj(x)为梁跨第j个梁段的振型函数,其中x∈[xj-1,xj).

综合上述裂缝处的性质及式(4),可得到梁跨内第j+1梁段与第j梁段振型函数的关系:

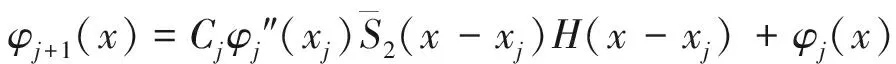
(5)

根据式(5),可得到同一跨内任何梁段振型函数之间的回归方程.梁跨第N+1梁段(最后一个梁段)与第1个梁段振型函数之间的回归方程为:

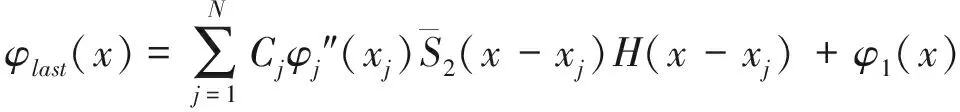
(6)

若图1中左侧为固定端,右侧为悬臂端,则悬臂梁的边界条件为:

固定端

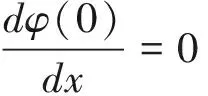
(7)

φ(0)=0

(8)

自由端

(9)

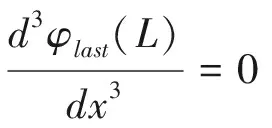
(10)

由式(9)、式(10)分析可知,φlast有且仅有梁跨的4个初始参数φ(0),φ′(0),M(0)和Q(0),故式(9)～式(10)可转化为仅含4个待定系数φ(0),φ′(0),M(0)和Q(0)的方程式.

悬臂梁的固定端支撑能够确定2个方程，即式(7)和式(8)；悬臂端支撑能够确定2个方程，即式(9)和式(10).因此,由支撑确定的方程总数为4个.梁跨内有4个待定系数需确定.

综合式(7)～式(10),可确定如图1所示的悬臂裂缝梁式结构动力特征方程:

[H]{u}=0

(11)

式中,[H]为式(7)～式(10)确定的维矩阵,{u}=[φ(0)φ′(0)M(0)Q(0)]T.

在得到悬臂裂缝梁式结构动力特征方程后,采用半区间-迭代方法[8]可求解出悬臂裂缝梁式结构的前几阶频率及与每阶频率对应的待定系数向量.把待定系数向量代入式(5)～式(6)便可计算出振型.

2 等截面裂缝梁式结构动力特性求解方法验证

作者与吉林大学课题组合作,参与了等截面悬臂空心矩形截面梁的动力特性实验.为了验证等截面裂缝梁式结构动力特性求解方法的正确性和可靠性,运用等截面悬臂空心矩形截面梁的动力特性实验结果,此悬臂梁的材料为钢材,弹性模量为2.06×1010Pa,密度为7 850 kg/m3.

空心矩形截面梁如图2所示,其几何尺寸为梁长L=1.8 m,t=0.006 m,d=0.006 m,h=0.05 m,b=0.1 m.

图2 空心矩形截面试验梁(m)Fig.2 Hollow rectangular section test beam(m)

采用钢锯在特定位置制造一定深度的裂缝,借助江苏东华测试有限公司生产的131 E型加速度拾振器和DH 5920型振动采集分析仪,利用锤击方法对试验梁进行激振,测试了多种裂缝工况下试验梁的自振频率.空心矩形截面试验梁测试现场如图3所示.

(a) (b)图3 空心矩形截面试验梁测试现场Fig.3 Test site of hollow rectangular section test beam

针对空心矩形截面试验梁,均测试了两种裂缝工况下的自振频率变化.

工况1:在距悬臂端0.3 m(x1=0.3 m)处有1条裂缝,裂缝相对深度(裂缝深度/截面高度)按5 %的间隔从0 %增长到30 %.

工况2:x1=0.3 m处的裂缝相对深度为30 %保持不变,在距悬臂端0.75 m(x2=0.75 m)处出现另一条裂缝,裂缝相对深度按5 %的间隔从0 %增长到30 %.

采用自振频率改变率RFCi来表征裂缝对自振频率的影响,自振频率改变率RFCi定义如下:

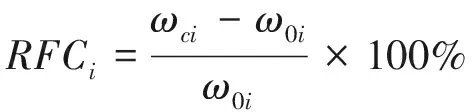
(12)

式中,ωci为裂缝梁的第i阶自振频率;ω0i为完好梁(无裂缝梁)的第i阶自振频率;RFCi为第i阶自振频率改变率.

空心矩形截面试验梁前两阶自振频率改变率测试结果如图4所示.

(a) 1阶自振频率改变率 RFC1(a) The 1st order natural frequency change rate RFC1 (b) 2阶自振频率改变率 RFC2(b) The 2nd order natural frequency change rate RFC2图4 不同裂缝工况下空心矩形截面试验梁的自振频率改变率Fig.4 Natural frequency change rate of hollow rectangular section test beams under different crack conditions

由图4可见,根据工况1和工况2，对于1，2阶自振频率，随着裂缝数量的增加，自振频率改变率数值明显减少.

当裂纹数不变时，裂缝相对深度从0 %增加到10 %，自振频率改变率的数值减小，速率逐渐增大；

裂缝相对深度在10 %至15 %之间，自振频率改变率的数值存在突变，突变之后自振频率改变率的数值减小，速率减小.

在不同裂缝工况下,空心矩形截面试验梁其前两阶自振频率改变率的试验结果与计算结果存在良好的一致性,这充分说明了本文提出的等截面裂缝梁式结构动力特性求解方法的正确性和可靠性.

3 结论

本文得到了等截面裂缝梁式结构动力特性的精确解，阐述了等截面裂缝梁式结构自由振动分析的正问题，基于悬臂钢梁动力特性识别基础数据,对等截面裂缝梁正问题的正确性进行了算例验证，研究了裂缝对等截面梁固有频率的影响.在数值计算的基础上,得出以下结论:

(1) 该方法的计算结果与实例数据吻合较好,验证了该方法的有效性和可靠性，在确定等截面梁的模型函数和建立整个系统的特征方程过程中,没有引入任何假设,通用性很好.

(2) 正问题曲线拟合精度很高，结果表明,本文提出的裂纹识别算法具有良好的识别精度.