基于LH-OAT方法的VG模型参数敏感性分析
2019-10-25孙兆军
秦 萍,王 正,孙兆军,禹 昭
(1.宁夏大学环境工程研究院,银川 750021;2. 宁夏大学土木与水利工程学院,银川 750021;3. 宁夏大学新华学院,银川 750021;4.宁夏(中阿)旱区资源评价与环境调控重点实验室,银川 750021)
0 引 言
VG(van Genuchten)模型是进行土壤水盐运移研究和土壤水力参数率定的重要参考依据,特别是在分析非饱和土壤动态水力特性与讨论土壤入渗等过程中,都取得了非常好的拟合效果[1-3]。
但是,VG模型属于非线性模型,待定参数较多,且影响VG模型参数的因素非常繁杂,导致不同地区不同结构的土壤显现出的VG模型参数截然不同[4]。再加上,这些参数存在的不确定性会在模型使用过程中产生积累效果,从而影响模型模拟结果的可信度[5]。因此,必须先率定出可信度较高的模型参数才能进行应用,但是在样本资料较少且不可靠的情况下进行率定时显得较为困难,对于这种情况,研究模型参数的敏感性就具有重要意义。通过模型参数敏感性的识别,可以为反演出可信度更高的参数提供更有力的保障,同时,也避免了盲目地进行参数的率定。
分析模型参数的敏感性是为了实现通过率定最少的参数同时得到最佳模拟结果的目的,通常有局部型和全局型两类敏感性分析方法[6]。就局部敏感性分析方法来说,其原理是每次选择一个或一类参数作为变量来检验模型拟合结果,而不考虑其他参数对其的影响作用,方法容易实现,但是方法得出的结果具有一定的片面性和偶然性[7,8]。而全局敏感性分析则是通过改变多个参数综合检测它们对模型运行结果的作用程度,用这种方法来分析非线性模型的敏感性具有较大优势。目前,常用的模型参数全局敏感性分析方法有扰动分析法[9]、Monte Carlo法[10]、Latin-Hypercube(LH)模拟法[11]以及LH-OAT(Latin-Hypercube One-factor at-a-time)法[12]等。但在土壤水力参数模型应用中,有关参数全局敏感性分析的成果尚不多见。本文针对土壤水力参数模型----VG模型,建立基于LH-OAT的全局参数敏感性分析方法,并利用2017年宁夏中部平原引黄灌区林地田间数据进行建模,以开展VG模型中有关参数的敏感性分析及模型校正。
1 研究方法
1.1 LH-OAT参数敏感性分析方法
本文所使用的LH-OAT方法是将由Mckay[13]等提出的LH抽样法与Morris[14]提出的随机OAT敏感性分析方法相结合产生的。其中,LH抽样法的基本思想是通过将满足均匀分布的多维参数均分为N层,并在保证每个参数仅采样1次的情况下抽样N次,最后随机组合成N个LH参数组。但是,通过较少频次的LH抽样法虽然能确保敏感性分析的高效性,但是当所有参数扰动时,并不能确定是哪个参数的变化引起了输出值的变化[15]。而OAT敏感性分析方法的基本思想则是通过运用控制变量法来对模型中的每个参数进行分析,也就是说当分析某一参数时假定其他参数保持一定,并对这一参数施加一定扰动,模型运行若干次之后,就可得到每个参数的敏感度,但是输出结果的摆动幅度与其他参数的取值密切相关[16]。此外,LH-OAT方法既发挥了它们各自的优点同时又规避了它们的缺点,其基本思想是通过对待分析参数中的每个参数分层并进行LH抽样以得到若干组数据,然后对每组数据进行敏感性分析,最终得到每组数据中每个参数的敏感度,最后求取每组数据敏感性的平均值。这种方法可以有效地识别出对模型结果产生作用的主要参数因子,极大地提高了模型参数的可信度。通常,归一化后的参数敏感性用下式计算[15]:
(1)
式中:S为模型输出,S=g(G1,G2,…,Gn);Gi为影响S的参数(i=1,2,…,n)。
敏感性的各类别如表1所示[17]。
表1 敏感度取值表
Tab.1 Sensitivity values table

分类敏感度指数敏感性Ⅰ|I|<0.05不敏感Ⅱ0.05≤|I|<0.02一般敏感Ⅲ0.2≤|I|<1.0敏感Ⅳ|I|>1.0极敏感
分析VG模型的m个参数的全局敏感性时,LH-OAT方法的实现步骤如下。
步骤1 在设定的m个参数值域内,采用LH抽样并随机组合生成N个LH抽样点;
步骤2 采用OAT方法生成N×(m+1)个参数组;
步骤3 针对步骤3生成的参数组,重复运行VG计算主程序N×(m+1)次,输出变量设定为土壤含水率θ(h),土壤相对饱和度Se,土壤非饱和导水率K(Se);
步骤4 针对各变量局部敏感度按照式(2)计算每个参数的相对敏感性。
Si,j=
j∈[1,n]
(2)
式中:Mj表示为第j个采样点对应的目标函数;ei为第i个参数;αi为参数ei的极小变化程度。
步骤5 取参数ei的最终敏感性指标Si为各个采样点ei参数的相对敏感性平均值,用式(3)计算。
(3)
LA-OAT方法的计算流程图如图1所示。

i为参数编号i=1,2,…,m;j为LH抽样层编号j=1,2,…,N图1 LA-OAT方法流程图Fig.1 Flow chart of LA-OAT method
1.2 VG模型
描述土壤特征曲线的模型很多,其中VG模型是与实测值吻合度最高的模型,其模型中的参数意义明确且受到了广泛应用。Mualem通过对大量室内试验进行研究得到土壤饱和导水率Ks与土壤水分特征曲线来估算非饱和导水率模型[18]。van Genuchten将其导出的水分特征曲线形式与Mualem模型相结合,得出了待定解析形式的VG模型。具体数学函数表达式为:
(4)
(5)
(6)
式中:θ(h)为土壤体积含水率,cm3/cm3;h为吸力水头,cm;θr为土壤残余体积含水率,cm3/cm3;θs为土壤饱和体积含水率,cm3/cm3;α、n是曲线性状参数,其中m=1-1/n,α是与土壤物理性质有关的参数,cm-1;K(Se)为土壤非饱和导水率,cm/min;
Ks为土壤饱和导水率,cm/min;Se为土壤相对饱和度;l为经验拟合参数,通常取平均值0.5。
1.3 模型中参数的不确定性
显然,从式(4)、式(5)、式(6)中可以看出,只要知道参数θr、θs、α、n、Ks、l就可求出VG模型中的土壤体积含水率、Se为土壤相对饱和度、K(Se)为土壤非饱和导水率。现在对上述6个参数分别作不确定性的初步分析。研究表明[19],θr在不同质地条件下的数值较小,而且变化范围不大,可以利用PTFs法进行测定,具有较强的确定性;而θs与θr存在共线关系,而且θs范围变化更小,也具有较强的确定性;α、n和Ks具有强烈的非线性关系,其中,不同土壤物理性质的α数值变化很大,存在很大的不确定性,而n的数值因土壤质地和土壤结构不同而变化,造成了其不确定性,另外Ks的数值较小,变化范围较大,而且随着α的增加,Ks快速增加,具有很强的不确定性。以研究区4种典型土壤的VG模型参数为例说明α与Ks之间的关系,数据如表2所示。为了解决α、Ks数值小且变化范围大的问题,本文采用了lgα、lgKs及lgKs/lgα来缩小参数的范围; 为一确定的经验参数,通常取0.5。
2 研究区域概况
本研究区为宁夏吴忠树新林场2017年林地田间试验区(38°36′N,105°56′E),面积为2.6 htm2。多年平均降水量约为260.7 mm,无霜期176 d,年平均气温8.3~8.6 ℃,属于中温干旱气候区,昼夜温差大,四季分明。试验地土壤类型为粗质灰钙土,土壤质地以砂壤土为主,有少数砂土和壤土,土壤密度为1.48~1.67 g/cm3,有机质含量较高,而深层土壤则以黏性土壤为主。试验时间为2017年11月7-27日,开展了土壤含水率和土壤物理性质的测定。试验内容主要包括:①土壤物理性质:根据试验地土壤采样点的分层取样样本,利用激光粒度仪分析试验地0~100 cm深度的土壤机械组成;②土壤含水率:采用烘干法分5层测定(0~20、20~40、40~60、60~80、80~100 cm),监测周期为6~8 d。
表2 研究区4种典型土壤的VG模型参数
Tab.2 Soil hydraulic parameters of the VG model for 4 soils

土壤类型θr/(cm3·cm-3)θs/ (cm3·cm-3)α/cm-1nKs/(cm·min-1) lgαlgKslgKs/lga砂土0.045 00.432 10.145 22.682 10.495 0-0.838 6-0.305 42.745 9砂质黏壤土0.100 00.398 40.124 52.281 40.243 2-0.906 5-0.614 41.475 4砂壤土0.065 00.435 20.059 41.487 50.021 8-1.226 2-1.661 50.738 0壤土0.078 00.467 30.036 31.566 50.017 3-1.443 7-1.761 20.819 7
模型设置时,土壤剖面厚度设定为100 cm,依据剖面土壤质地分为0~60 cm(砂土层)和60~100 cm(黏土层)的2个水平分层,记为a、b层,初始条件为模拟初始日期的实测土壤含水率。
3 分析与讨论
VG模型需要率定的参数有θr、θs、α、n、Ks、l等。本研究VG模型取值依照RETC软件进行确定,各个参数的取值范围如表3所示。
表3 VG模型参数取值范围
Tab.3 The range of the parameters of the VG model

土壤类型θr/(cm3·cm-3)θs/(cm3·cm-3)α/cm-1nKs/(cm·min-1)砂土0.045 0~0.057 00.428 5~0.430 30.036 3~0.145 21.890 2~2.683 20.073 6~0.495 0砂质黏壤土0.068 0~0.100 00.378 7~0.381 20.008 0~0.390 01.091 5~1.482 50.003 3~0.021 4
本文针对VG模型不同的输出结果(θ(h)、Se、K(S3)),分别计算土壤a层、b层的θr、θs、α、n、Ks、l等参数,共获得了11个参数的敏感性排序结果,如表4所示。
按照表1给出的敏感性取值,极敏感参数,排序为1;敏感参数,排序为2~6;一般敏感参数,排序为7~11;不敏感参数,排序为12。取出各参数排序的最小值作为全局敏感性分析的排序结果,如表5所示。
表4 参数敏感性顺序
Tab.4 The order of parameters sensitivity

序号123456 参数θsa、θsbθra、θrbαa、αbKsa、Ksbna、nbl
注:下标a、b表示土层
表5 参数敏感性分析结果
Tab.5 The results of sensitivity analysis
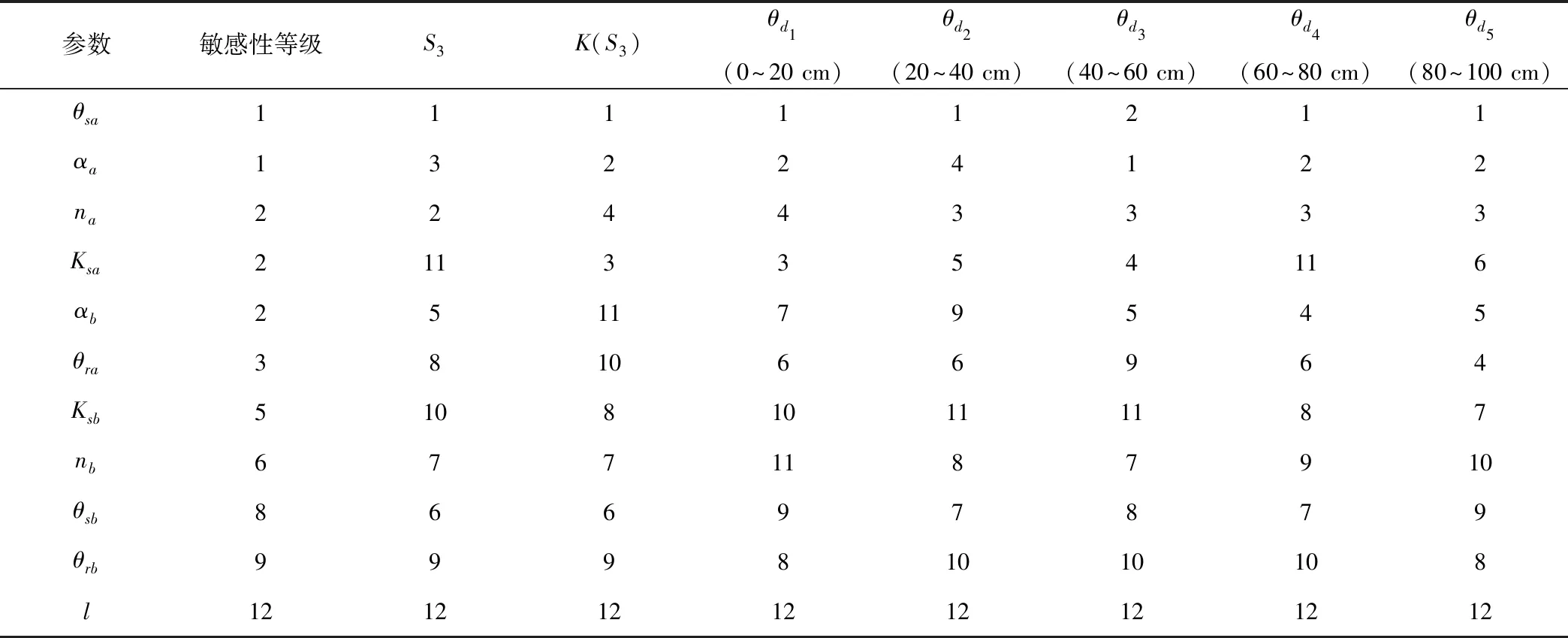
参数敏感性等级S3K(S3)θd1(0~20 cm)θd2(20~40 cm)θd3(40~60 cm)θd4(60~80 cm)θd5(80~100 cm)θsa11111211αa13224122na22443333Ksa2113354116αb251179545θra381066964Ksb510810111187nb6771187910θsb86697879θrb99981010108l1212121212121212
由于模型中各个参数参与的过程不同,对于不同输出变量的敏感性也有较大差异,全局敏感度的柱状图如图2所示。

图2 全局敏感度 Fig.2 The values of global sensitivity
另外,分别计算各个参数对不同输出变量敏感度的平均值作为该参数的全局敏感度,如图3所示,相比较而言,极敏感参数的敏感度指数明显大于敏感参数和一般敏感参数,与表1所指出的数据范围相一致,而不敏感参数的全局敏感度为0。以Se为输出变量时,其对θsa、αa和na呈高度的敏感性,而对αb、θra、nb和θsb表现出较高的敏感性,对Ksa、Ksb和l表现为一般敏感或不敏感。以K(Se)为输出变量时,其对θsa表现最为敏感,对αa、na、Ksa表现出较高的敏感性,对其他参数敏感性较弱。
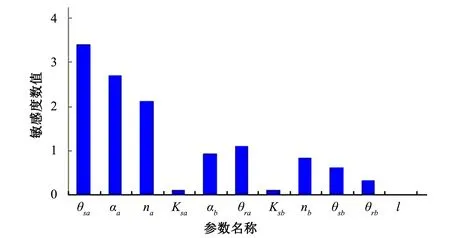
图3 输出为Se的全局敏感度Fig.3 The values of global sensitivity

图4 输出为K(Se)的全局敏感度Fig.4 The values of global sensitivity
下面分析输出为土壤含水量时的模型全局敏感度,结果如图5所示。本研究的试验区采用漫灌方式,水分充足导致土壤分层含水量主要与土壤水力参数相关。考虑到受土壤蒸发和植物需水等因素影响,再加上土壤样本的监测点主要集中在a层,所以土壤含水量对a层的土壤水力参数均呈现出较强的敏感性,土壤水分特征曲线的主要参数θsa、αa和na表现出强烈的敏感性,同时b层土壤部分参数也对a层土壤含水量输出结果呈现出了一定的敏感性,这是因为地下水的盈亏会导致底层土壤产生渗漏和水分补充等过程,从而导致了底层土壤水力参数对上层土壤的含水量产生作用。
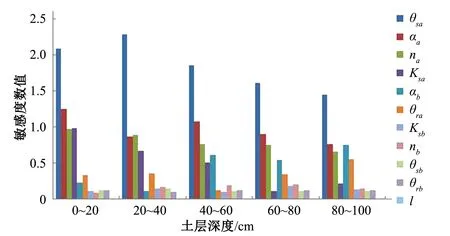
图5 不同深度土层含水量的全局敏感性Fig.5 Global sensitivity of soil water content at different depths
4 模型校验
为了得到更好地拟合效果,对上述敏感参数实施手动修正,以期达到最佳拟合效果。经过多次调整,修正后的敏感参数值如表6所示。将修正后的敏感参数与极敏感参数一起应用于VG模型中,模型模拟效果采用平均相对误差(MRE)、均方差(RMSE)及决定系数(R2)来评价[19]。某样本点修正后的土壤含水率实测值与模拟值对比如图6所示。
通过对比后容易得知,不同监测时期不同土层深度的土壤含水率有显著变化,且模拟值较好地反映了实测值的变化趋势,吻合度较高。由于第1次采集土样发生在冬灌后的第7 d后,且上层土壤受蒸发、下渗和植物吸水等因素的影响,所以土壤下层的含水率要高于上层。随时间的推移,各层的土壤含水率均有所下降,这也与实际相符合。
表6 VG模型参数对比
Tab.6 The range of the parameters of the VG model

土壤类型θra/(cm3·cm-3)θsa/ (cm3·cm-3)θsb/ (cm3·cm-3)αa/cm-1αb/cm-1nanb修正前0.0450.436 80.379 20.040 80.038 61.3791.400修正后0.0510.509 80.382 40.042 60.047 31.4061.366

图6 土壤样本含水率实测值与模拟值对比 Fig.6 Comparison between the simulated and the measured value
表7 VG模型检验指标
Tab.7 The test indexes of VG model

土壤类型MRE/%RMSER2Se2.648 70.196 80.924 3K(Se)3.023 50.236 50.864 4土壤含水率1.960 70.046 60.974 4
由表7的VG模型检验指标可以看出,MRE、RMSE都较小,而且R2接近于1,较为理想,因此模拟结果可以接受。结合土壤样本含水率实测值与模拟值对比(图6)、模拟检验指标(表7)可知,修正后的敏感参数应用于VG模型能较好地模拟该研究区内的不同土层含水率。
5 结 语
本研究将LH-OAT方法与VG模型相结合,讨论了适用于VG模型参数全局敏感性分析方法,并将其应用于宁夏引黄灌区2017年的土壤含水率数据进行了方法检测和参数敏感性分析,并对分析后的敏感参数进行了修正。结论如下:
(1)VG模型中参数θsa、αa和na表现极为敏感,而αb、θra、nb和θsb较为敏感,Ksa、Ksb和l表现为一般敏感或不敏感。
(2)定量讨论了参数对各输出变量(θ(h)、Se、K(Se))的敏感性程度,对不同输出呈现显著的差异。
(3)根据全局敏感性分析的结果,修正敏感参数后对模型进行了校验,校验的结果较为理想。该方法具有很强的普适性,为提高后续模型参数率定效率提供了依据。
