目标运动角速度的火控滤波改进方法

许娣，张逊

(江苏自动化研究所，江苏 连云港 222061)

0 引言

随着军事的发展，新型反舰导弹具有飞行速度快、战术运用活、突防能力强及隐秘性强等特点，例如西方的“安斯”，俄罗斯的“宝石”及要破“宙斯盾”的“白蛉”等[1-3]。反舰导弹的高速和机动等的突防性能特点，迫使末端防御武器系统提高快速反应能力，从而提高了对滤波解算快速收敛的要求[4-6]。

现代火控雷达对目标的跟踪过程，不仅能够量测目标的位置信息，还可以获得目标的角速度运动信息[7-8]。因此，近些年来，许多国内外的学者和研究人员将目标角速度引入到火控滤波技术中，并取得了一定成效[2]。引入目标角速度到火控滤波算法中，大幅度的缩短了滤波收敛时间[9]。但是对于进一步提高火控解算精度有待探究。本文从火控解算精度着手，深入分析位置量测误差对目标速度的影响，开展目标运动角速度的火控滤波技术研究。

基于目标运动角速度的火控滤波技术[9-10]，通过跟踪传感器在跟踪目标时提供的目标角速度信息，经过一系列变换得到地理坐标系的目标运动速度，引入到火控滤波算法中，缩短了滤波收敛时间。本文正是在基于目标运动角速度火控滤波技术基础上，基于工程实际考虑，分析位置量测信息对于滤波解算影响，并提出一种基于最小二乘预处理技术的改进方法，提高对滤波解算的精度。

文章首先在对瞄准线坐标系目标运动角速度转化为地理坐标系线速度的基础上，分析目标位置量测信息对计算目标线速度的影响。将目标速度引入到卡尔曼滤波算法中，分析位置量测信息对滤波解算结果的影响。随后为降低位置观测噪声对滤波解算的影响，提出了一种基于最小二乘量测预处理的滤波改进方法。最后通过仿真典型运动航路，直观分析位置信息对基于角速度滤波结果的影响，表明提出的改进方法具有可行性及实际应用价值。

1 基于角速度滤波方法

基于目标运动角速度的滤波技术，已知跟踪传感器提供的量测径向距离、偏角及倾角等位置信息及横滚角速度、侧向角速度及俯仰角速度等角速度信息，通过瞄准线坐标系角速度转换地理坐标系线速度方法[11]，得到目标线速度；将目标的线速度信息引入到卡尔曼滤波算法中，完成对目标的火控滤波解算。

计算地理坐标系目标线速度方法，可以通过下面公式得到[5]

(1)

图1为目标角速度量测关系示意图。

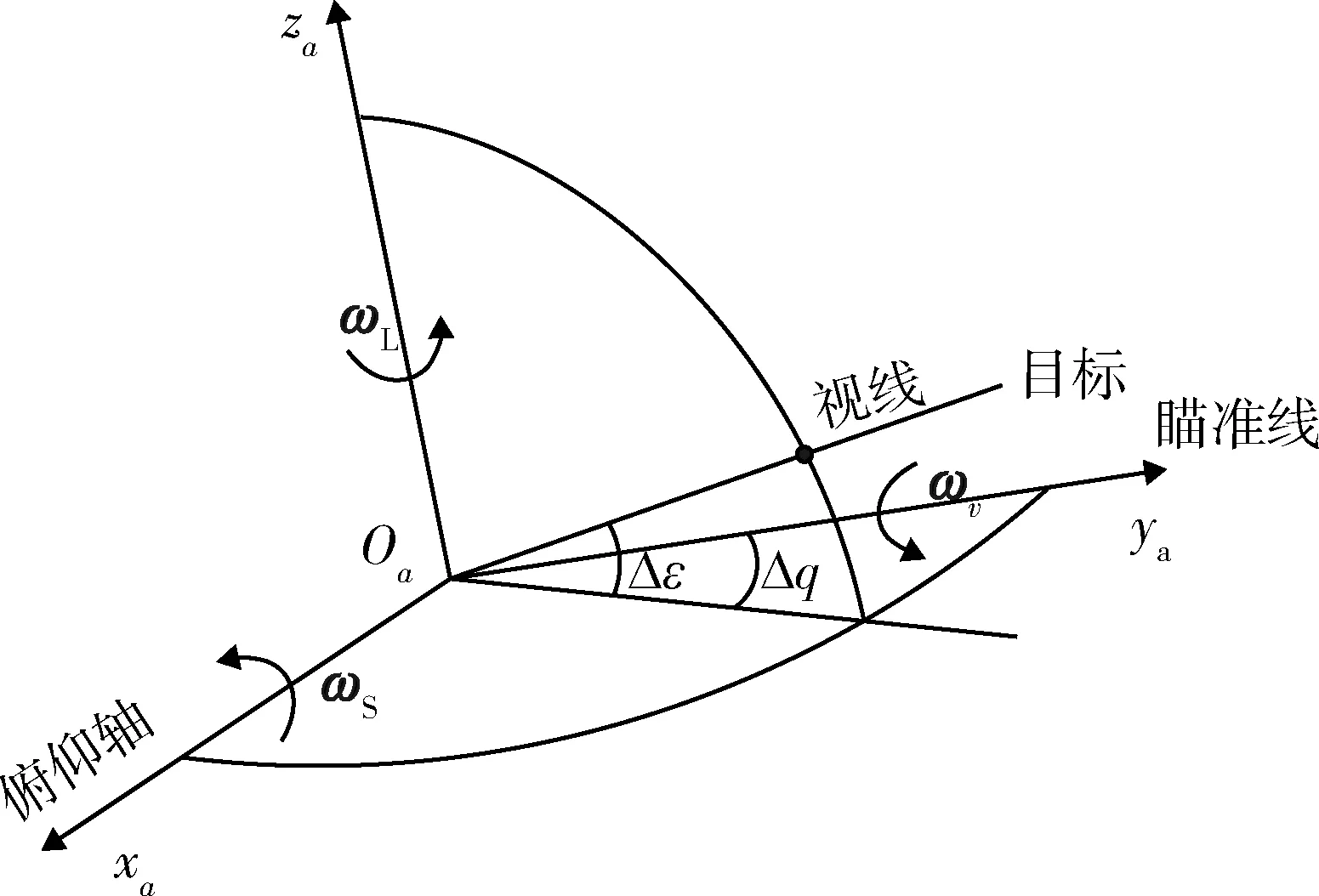
图1 目标角速度量测关系图Fig.1 Target angular velocity measurement diagram

根据式(1)计算得到目标地理坐标系的线速度，引入到卡尔曼滤波算法中[12-13]。

状态方程:

S(k+1)=Φ(k+1,k)S(k)+w(k),

(2)

式中:S(k)为k时刻目标状态向量，即由目标的位置、速度、加速度等表示出来，以y轴为例，S(k)=(y(k),vy(k),ay(k))；Φ(k+1,k)为目标从k时刻状态到k+1时刻的状态转移矩阵;ω(k)为k时刻系统模型的噪声。

观测方程:

Y(k)=Θ(k)S(k)+V(k),

(3)

式中:Y(k)=(y(k),vy(k))为k时刻的二维观测向量;Θ(k)为k时刻的状态向量到实际观测的转移矩阵;V(k)为k时刻的量测噪声。

根据卡尔曼滤波递推关系，得到卡尔曼滤波算法基本过程如下:[10]

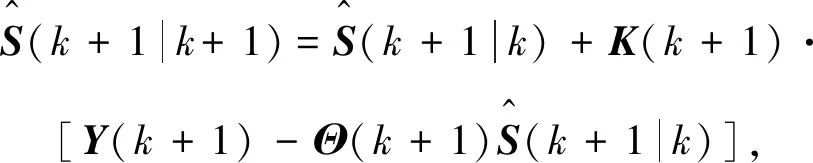
(4)

K(k+1)=P(k+1|k)ΘT(k+1)[Θ(k+1)·
P(k+1|k)ΘT(k+1)+R(k+1)]-1,

(5)

P(k+1|k+1)=[I-K(k+1)·

Θ(k+1)]P(k+1|k).

(6)

2 位置量测对计算线速度影响分析

基于目标运动角速度的滤波技术，卡尔曼滤波算法中的观测向量Y(k)为二维向量，即目标位置和速度信息，其中目标速度信息由式(1)计算得到。

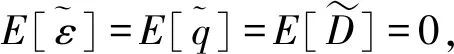
(7)

(8)

2a0a1(-ωmyωmxΔε2+ωmyωmzΔεΔq+

2a1a2(-ωmyωmzΔq2+ωmyωmxΔεΔq+

(9)

同理可得

2a3a4(-ωmyωmxΔε2+ωmyωmzΔεΔq+

2a4a5(-ωmyωmzΔq2+ωmyωmxΔεΔq+

(10)

(-ωmyωmxΔε2+ωmyωmzΔεΔq+ωmxωmzΔε-

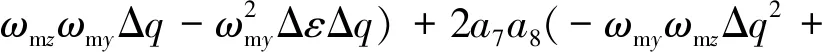
(11)

式中：(Dm,Δqm,Δεm)为观测位置信息；(D,Δq,Δε)为理论实际位置信息；ωmx，ωmy及ωmz为跟踪器测得3个角速度分量。

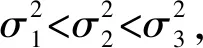
图2 俯仰角速度与目标速度误差关系图Fig.2 Relation diagram of velocity error and pitch angle velocity

由图2可知，一定的位置量测误差，俯仰角速度越大，计算得到目标线速度误差越大；对于3类不同的位置量测误差曲线可以得到，当俯仰角速度不为0，位置量测误差越大，计算得到线速度误差越大。当俯仰角速度为定值，得到位置量测误差与目标线速度误差关系，如图3所示。

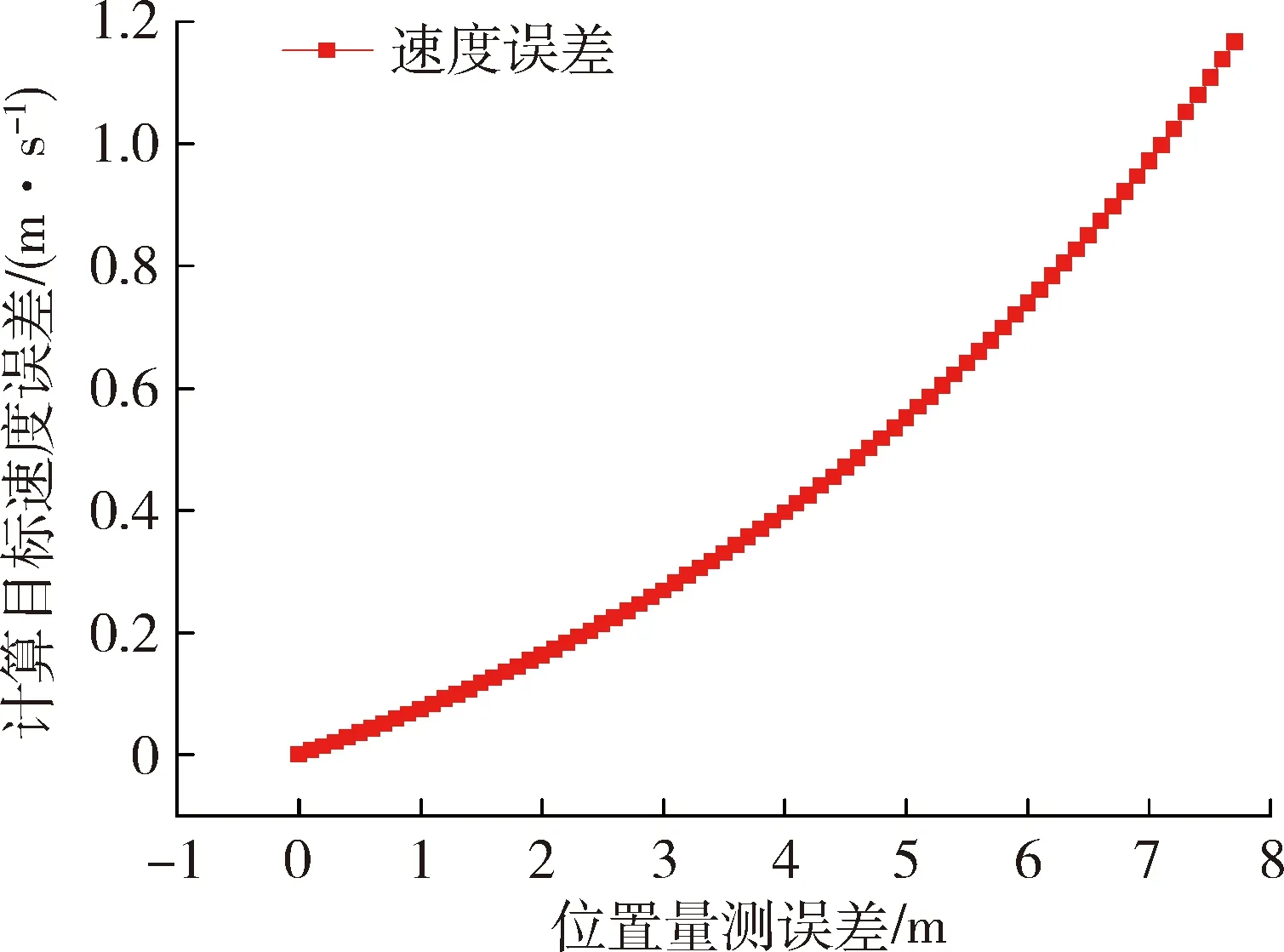
图3 目标量测误差与速度误差关系图Fig.3 Relation diagram of velocity error and target measurement error

3 基于最小二乘预处理的改进方法

由第2节中位置量测对计算线速度影响分析可知，位置量测误差对计算线速度影响明显，若采用位置量测信息计算目标线速度，而引入到卡尔曼滤波算法中，滤波解算结果受位置误差影响，式(4)中得到的滤波结果为

(12)

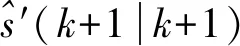
在工程实际应用中，对于末端防御武器系统而言，跟踪传感器跟踪来袭目标，目标距离越近，目标角速度越大，特别当目标在过捷阶段，角速度增大，由图2可知，目标速度误差增大，进一步降低了火控滤波解算精度及稳定性。

迫于工程实际无法获得理论位置信息，又需要克服位置量测噪声对滤波解算结果的影响，尽可能减小计算目标线速度所采用的位置量测噪声。基于此原则，采用基于最小二乘的预处理方法，对位置量测数据进行预处理，将预处理的位置信息代替原位置量测信息，计算目标线速度

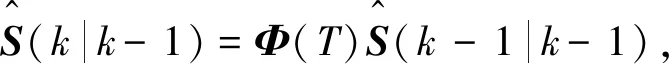
(13)

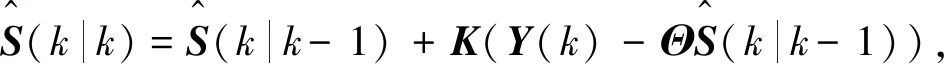
(14)

式中[6]：

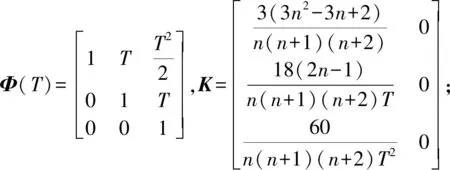
(15)

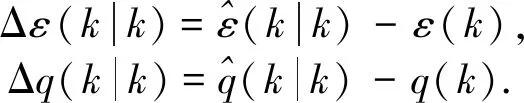
(16)

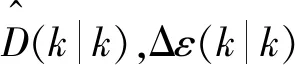
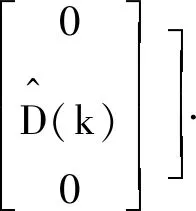
(17)

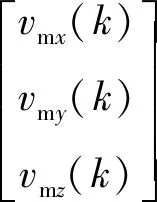
4 仿真计算

为验证瞄准线坐标系目标运动角速度转换地理坐标系线速度方法中位置量测信息对目标速度的影响，及改进方法的切实有效性，开展了典型目标航路的仿真。针对有噪声的位置量测信息下的有/无改进滤波方法进行了对比分析。

仿真2种典型目标航路，针对计算的目标线速度误差结果、滤波解算速度误差结果对比分析，如图4，5所示。

航路1：目标初始位置距离为7 km，目标速度为300 m/s，运动样式为匀速直线运动。

航路2：目标初始位置距离为10 km，目标速度为680 m/s，运动样式为比例导引运动。

在目标航路中添加不同马尔可夫噪声：噪声1表示航路位置数据添加的噪声幅值与现役跟踪传感器量测精度相当；噪声2表示航路位置数据添加的噪声为噪声1的2倍。

采用上述不同方法得到滤波误差结果，如图6，7所示。

图4 航路1的目标速度误差曲线Fig.4 Target velocity error curve of route 1

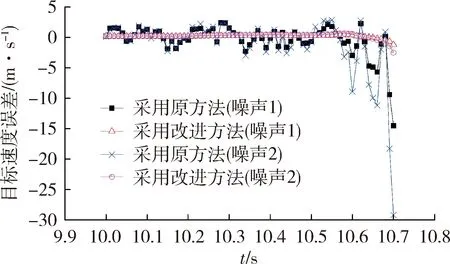
图5 航路2的目标速度误差曲线Fig.5 Target velocity error curve of route 2

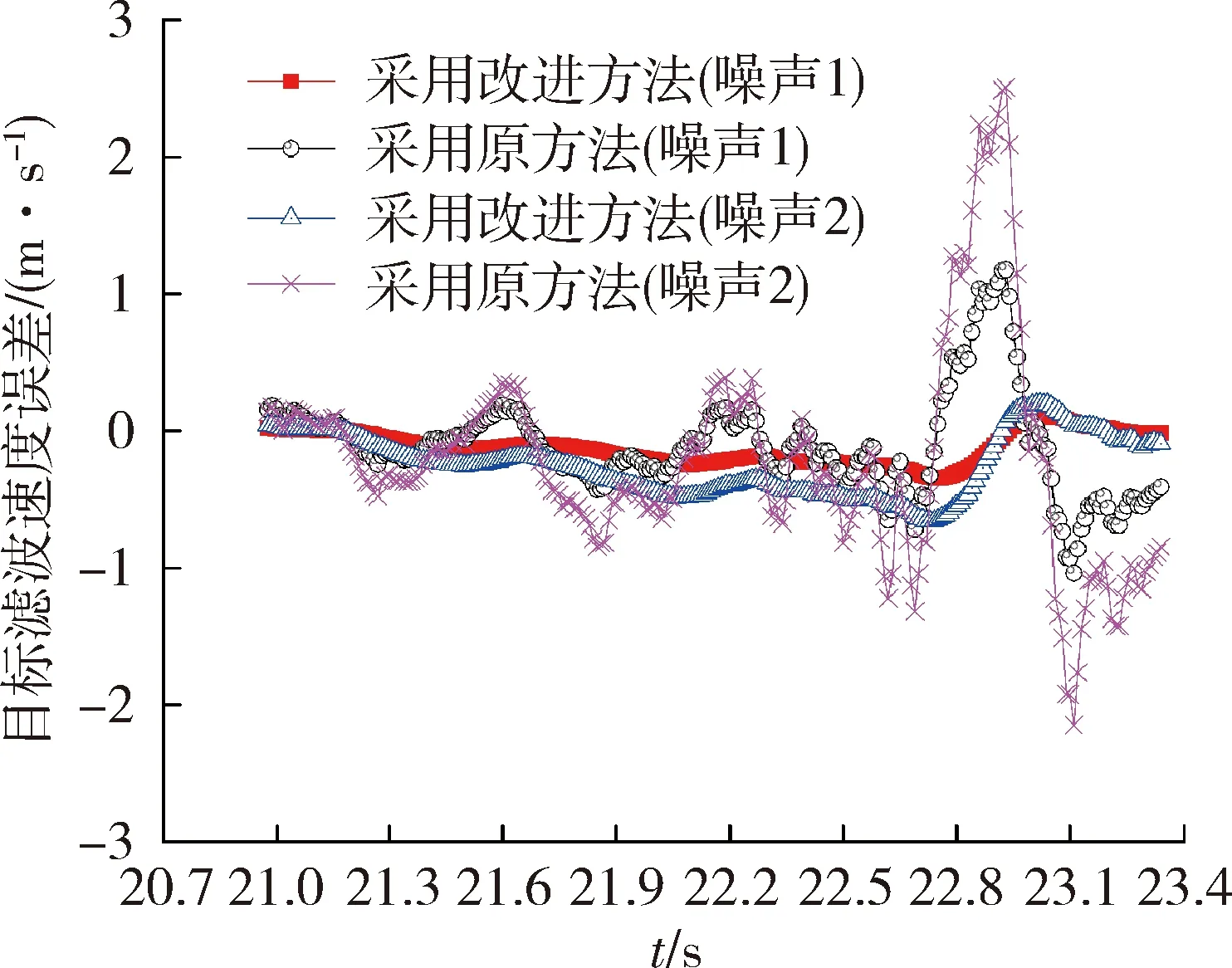
图6 航路1的滤波速度误差曲线Fig.6 Filter speed error curve of route 1

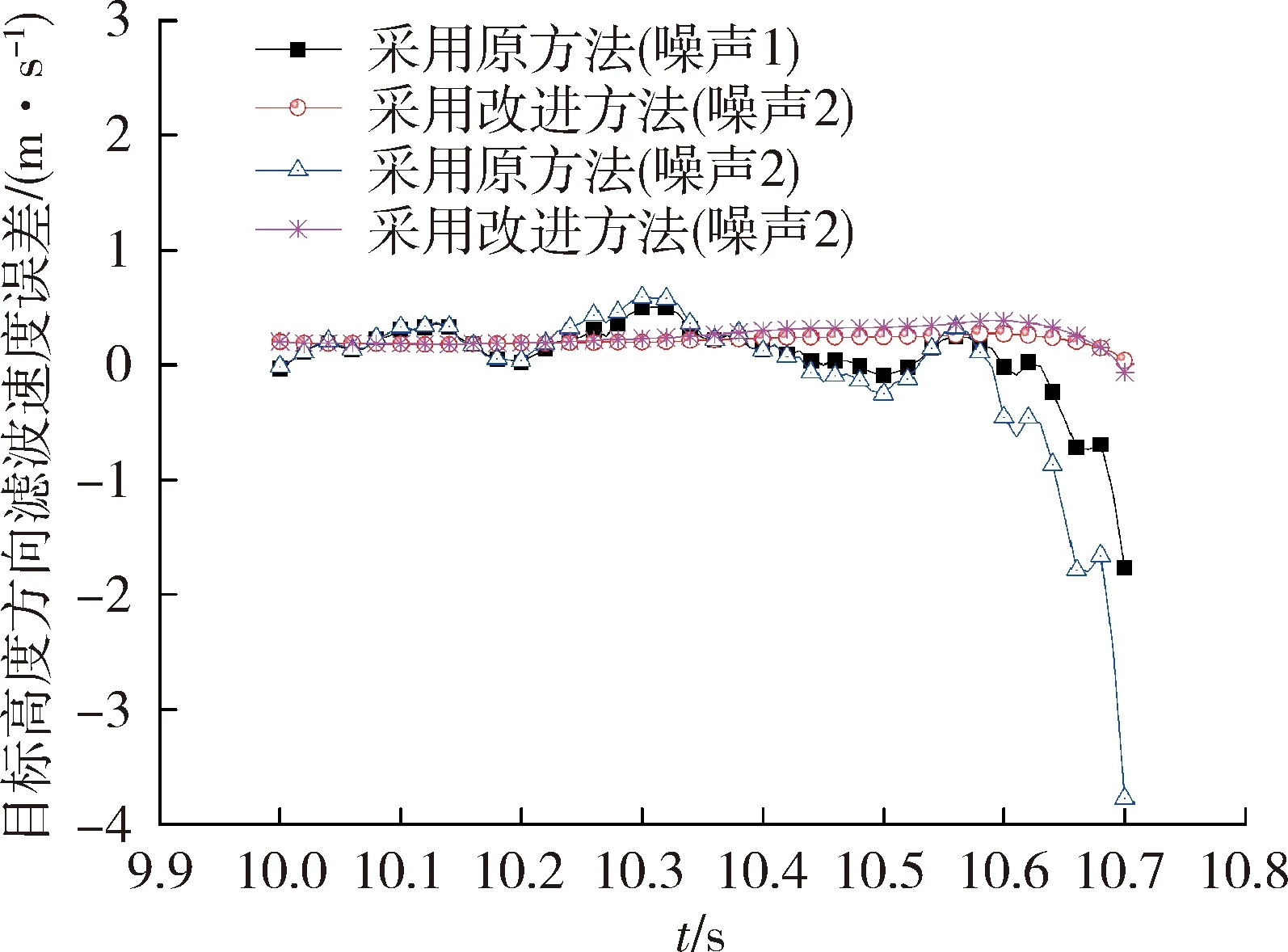
图7 航路2的高度滤波速度误差曲线Fig.7 Filter speed error curve of route 2

仿真结果表明，采用基于最小二乘预处理方法，位置量测误差对目标线速度影响明显降低；对于引入速度量测的卡尔曼滤波算法，提高了滤波解算的精度及稳定性，验证了改进方法的切实有效性。

5 结束语

本文通过分析位置量测噪声对目标线速度及卡尔曼滤波解算的影响，提出了一种目标运动角速度的火控滤波改进方法。结合工程应用进行仿真验证，表明有噪声的位置信息会降低滤波解算的精度及稳定性，验证了目标运动角速度的火控滤波改进方法的切实有效性。

采用最小二乘平滑预处理的方法，可以显著消除位置量测信息中的大部分噪声，明显改善滤波水平。虽然最小二乘预处理不能完全消除位置测量噪声，但由于工程应用中无法得到目标真实位置，本文方法无疑具有很好的指导价值。