基于BPR改进函数与V/C比的自动驾驶汽车路况预测与分析
2019-10-24汤莉莉谢加良
汤莉莉,谢加良
(集美大学理学院,福建 厦门 361021)
1 研究背景
随着无人驾驶汽车技术逐步成熟,对普通机动车和无人驾驶汽车进行有效的疏导与规划,合理分配城市交通资源,提高城市道路的利用率具有现实意义。作为出行者选择出行路线的重要依据,路况预测、交通流分析、交通拥堵评价[1-2]等方法,已成为研究城市交通问题的主要手段。学者们一般采用BPR函数、V/C比、事故率等指标量化,实现路况预测、交通流分析和交通拥堵评价等。
BPR函数[3]是美国公路局对大量路段进行交通调查后通过回归分析所得到的,可用于量化交通阻抗以度量车辆在运行中通达程度及顺畅程度。随后,不少学者针对函数中β值过高而引起的精度值过低及在饱和度较低时运行时间变化幅度小等问题对其进行了修正[4-7]。近年来,不少学者对BPR函数进行修正,使其精度大幅度提高[8-9],目前已被广泛采用于各种交通网络研究。V/C比是每小时交通量与相应路段通行能力的比值,国内外学者通过对事故率与V/C比之间的关系进行研究发现[10-12],事故率和V/C比之间存在密切的联系,可作为事故预测和预防的一个重要指标。
本文利用美国华盛顿州Thurston、Pierce和Snohomish等地的路段起点、路段终点、平均每日车流量、道路匝数等数据(2017 MCM数据)[13],基于BPR改进函数与V/C比建立相关数学模型,以实现对自动驾驶汽车路况的预测与分析,从而为自动驾驶汽车投入实际应用提供理论支撑和决策依据。首先,建立自动驾驶汽车所占比出行效率模型;然后,考虑车辆彼此之间的交互作用,建立自动驾驶汽车所占比安全性模型;最后,基于数据求解模型、检验模型,确定出路段最优自动驾驶汽车所占比。在此基础上,进一步实证分析,检验该模型的合理性。
2 构建自动驾驶汽车所占比出行效率模型
构建车辆路段行程时间模型,基于数据求解、检验车辆路段行程时间模型,分析以自动驾驶汽车所占比为变量的车辆出行效率。
2.1 构建车辆路段行程时间模型
由BPR函数模型可得,当流量为V时一辆车通过该路段的行程时间t为:
(1)
其中,α,β均为参数,α=0.15,β=4[14]。针对β值过高容易引起精度值过低等问题,叶枫[8]基于BP神经网络对真实路段行程时间和路段流量进行拟合,改进了BPR函数的缺陷。BP神经网络具有很强的非线性映射能力,相比于传统的统计方法,在数据复杂情况下准确性更高。经改进后得到参数α=0.780 7,β=1.423 9[8],使得模型反应信息更加准确,精度提升23.37%。公式(1)中道路无阻碍时的通过时间t0为该路段的长度与最大限速之比:
(2)
道路的实际通行能力c为:
(3)
其中,αc为道路系数,n为该地段车道的匝数,p为自动驾驶汽车所占比,CB为道路的基本通行能力[15]。道路基本通行能力与最小车头距和车头最小间隔关系如下:
(4)
其中,v为行车速度,l0为车头最小间隔。
由此可推导得出:
(5)
2.2 求解车辆路段行程时间模型
结合实际情况和相关研究,本文给出如下常规性假设:(a)路段上车辆的平均通过速度v=48 km·h-1;(b)车头最小间距l0=40 m;(c)道路系数αc=0.85;(d)路段上车辆最大限速vmax=60 km·h-1。
基于上述假设,由式(5)得:
(6)
基于数据求解模型,通过描点法得出如下自动驾驶汽车占总汽车的比例p与平均一辆车通过这个路段的用时t的函数图像。
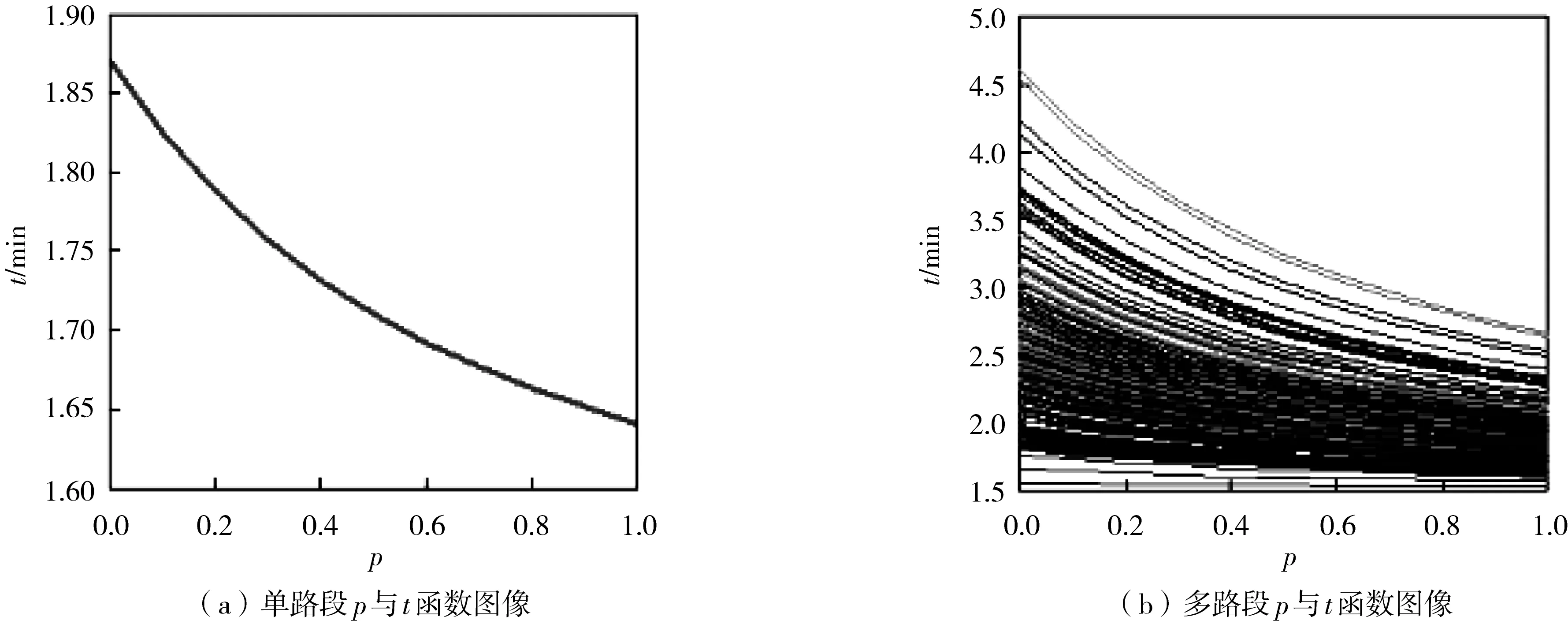
图1 p与t函数图像
图1(a)是路段1的t-p图,即s=1.5 km,n=6,路段每小时可以通过的最大交通实体数V=2 700,图1(b)为数据中所有路段的t-p图。由图1可知,随着自动驾驶汽车所占比的增加,平均一辆车通过路段的时间t就会减少,并且t的减少速度随着p的增加越来越小。
从出行的效率方面考虑,适当增加道路自动驾驶汽车所占比,可有效提高出行效率,减轻交通压力。
2.3 鲁棒性检验
对上述模型可能的误差源道路系数αc和平均行驶速度v进行敏感性分析。固定所有非分析参数的值,比较分析参数取不同值时的结果变化。
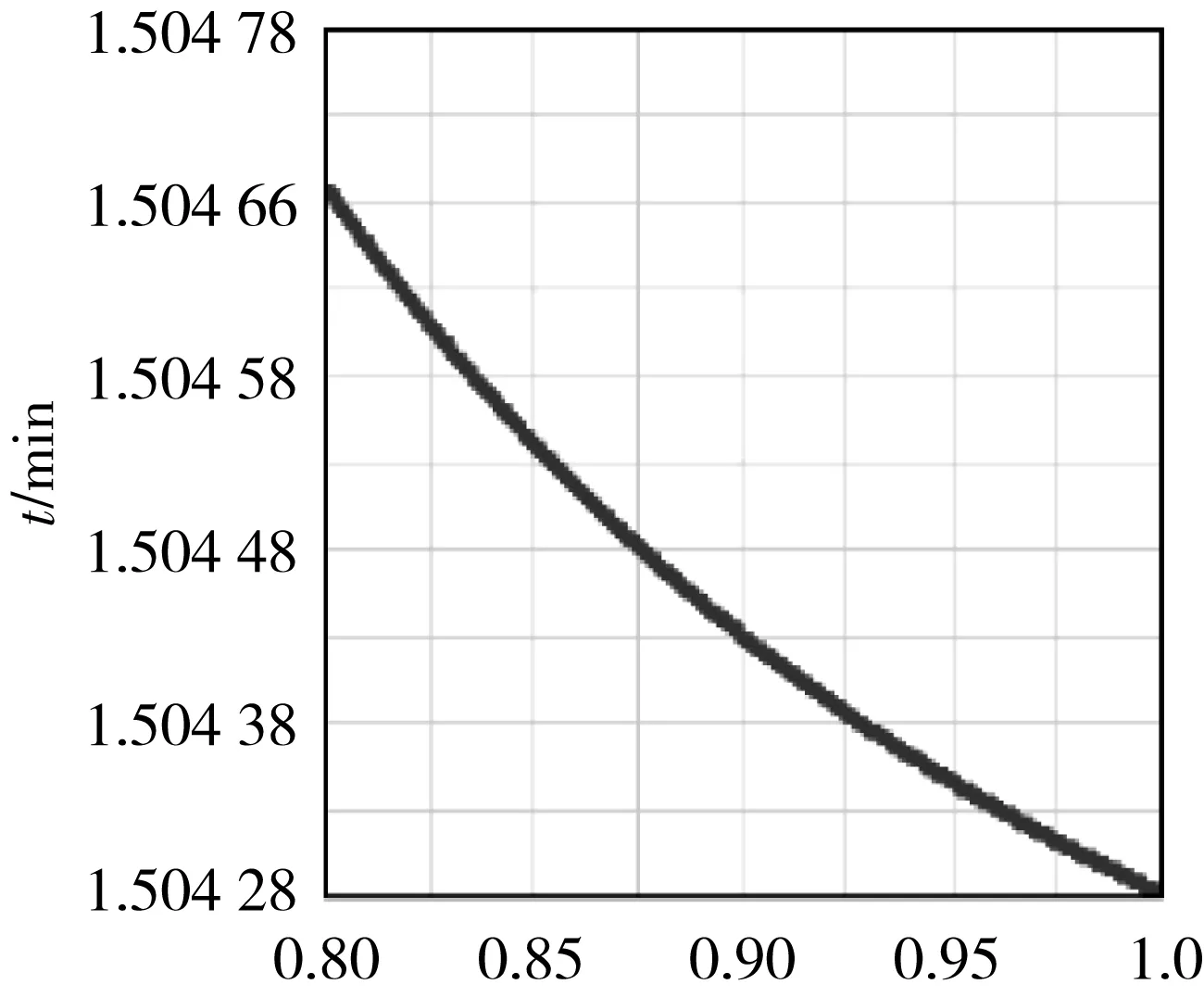
αc(a)αc-t
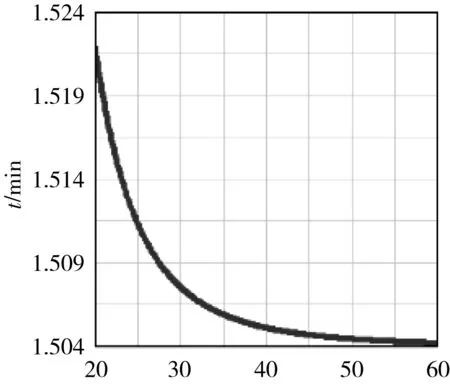
图2 参数αc及v变化的行程时间图
由图2(a)可知,当其它非分析参数固定不变时,行程时间随道路系数增加而减少。由图2(b)可知,当其它非分析参数固定不变时,行程时间随车辆平均通行速度增加而减少。
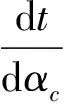
(7)
(8)
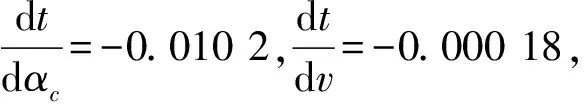
平均速度v的敏感性:
由上述敏感性分析可知,若道路系数αc比预期增长10%,则平均一辆车通过的时间将降低3.46%;若平均速度v比预期增长10%,则平均一辆车通过的时间将降低0.061 3%。由此可知,速度变化对模型结果影响甚微,而道路系数可经由专业人员进行测定,因此该模型具有良好的鲁棒性。
3 构建自动驾驶汽车所占比安全性模型
通过构建V/C比与事故率关系模型,基于数据求解、检验模型,预估自动驾驶汽车所占比增加所引起的安全问题。
3.1 构建V/C比与事故率关系模型
由文献[10]中V/C比与事故率CR关系模型,可得其关系函数为:
(9)
V/C比指路段每个小时内实际的交通量与实际通行能力的比值。由公式(3)和(4)可知高速公路的实际通行能力c为:
(10)
综合以上公式推导得:
(11)
3.2 求解V/C比与事故率关系模型
此处做出与第2.2节相同的假设,并基于数据求解模型。此处以路段名为1的数据为例求解,即V=2 700,l0=40,n=6,v=48,αc=0.85。由此绘制出二者的关系图,以便直观了解自动驾驶汽车所占比p与每百万公里的事故发生率CR的关系,如图3所示。
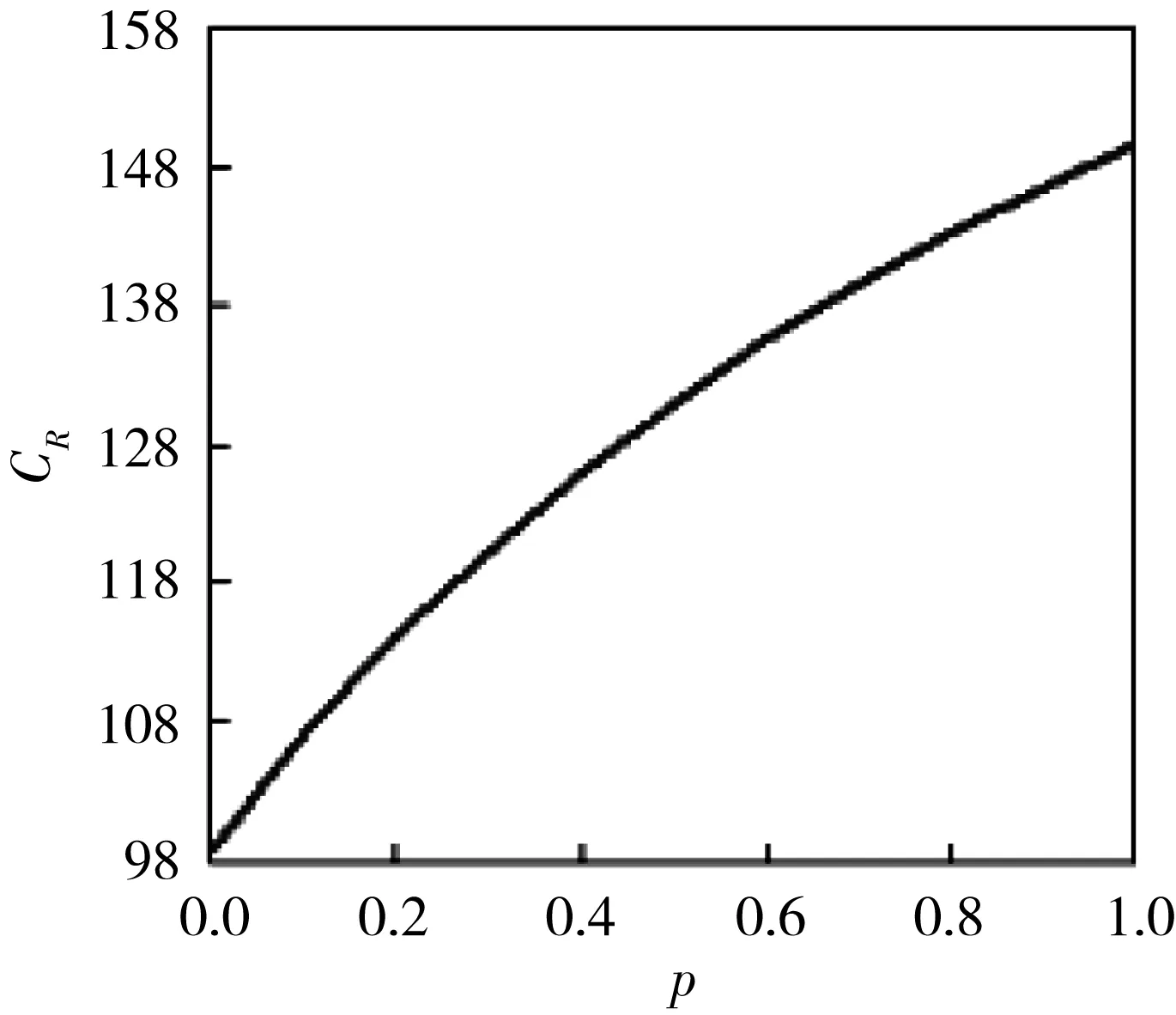
(a)单路段CR-p图
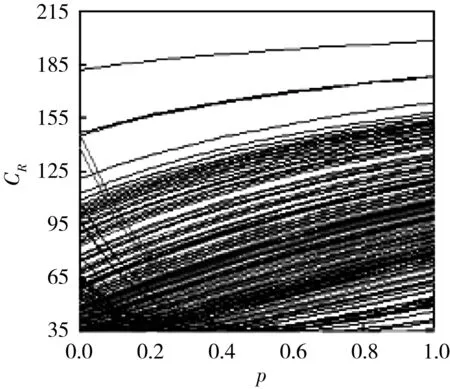
图3 事故率随自动驾驶汽车所占比变化图
图3(a)是路段1的CR-p图,图3(b)为数据中所有路段的CR-p图。由图3可知,自动驾驶汽车所占比p增加,大部分路段事故率呈上升趋势(下称“上升趋势路段”),并且CR的增加速度随着所占比p的增加越来越小。部分路段事故率呈现U型趋势(下称“U型曲线路段”)。对U型曲线路段进行详细分析后发现这些路段都有着一个共同特点:比起其他具有相同车道数的路段来说,它们所拥有的日均流量较大。
因此,随着自动驾驶汽车所占比的增加,车辆间的交互次数增加,大部分道路发生的事故率CR增加,而小部分的拥堵路段的事故率会呈现U型趋势。因此,从安全角度考虑不宜过度提高路段自动驾驶汽车所占比。
3.3 鲁棒性检验
为了检验模型对车辆平均通行速度v的敏感程度,本文对其进行敏感性分析。模型中事故率CR随平均速度v变化情况如图4所示。
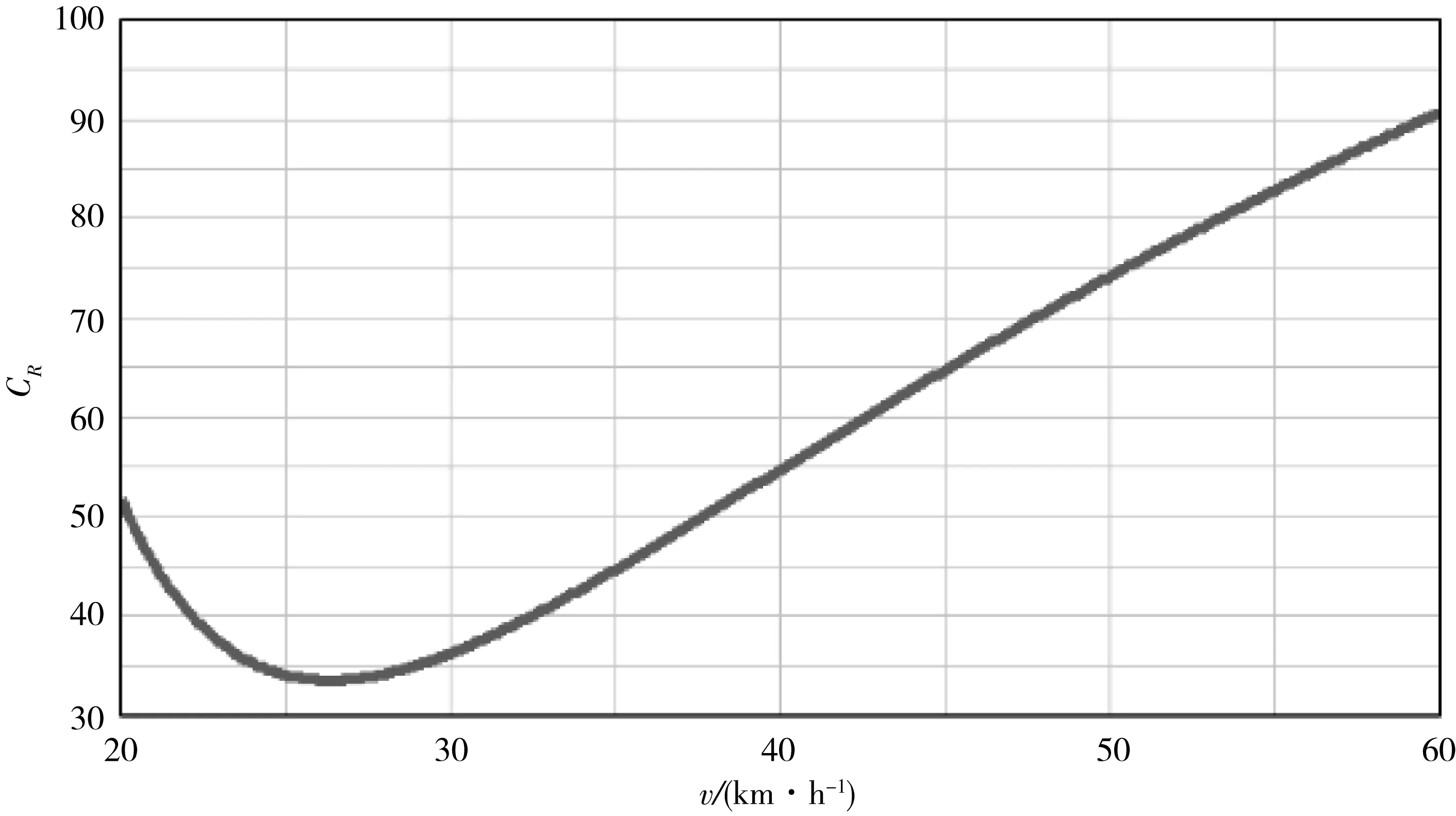
图4 事故率随平均速度变化图
由图4可知,当其它非分析参数固定不变时,事故率随车辆平均通行速度的增加呈先减少后增加的趋势,当车辆平均通行速度在20~30 km·h-1时,事故率有最低点。
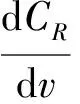
(12)
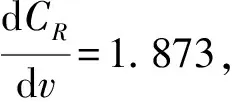
从上述的敏感性分析可以看出,如果车辆平均通行速度v比预期增长10%,则每百万公里的事故发生率将增加12.75%,可以看出平均通行速度为敏感参数,因此应该对各路段的车辆平均通行速度进行较为精确的测量,从而减少误差。与此同时,可得出平均通行速度的减少对于预防交通事故有较为明显的作用。
4 确定路段最优自动驾驶汽车所占比
由2.2节和3.2节可知,数据中的路段可分为两类:一类为U型曲线路段,一类为上升趋势路段。下面针对这两类路段分别建立模型,求解路段最优自动驾驶汽车所占比。
4.1 求解U型曲线路段最优自动驾驶汽车所占比
4.1.1 构建U型曲线路段最优p值求解模型
4.1.1.1 道路的事故率
由公式(11),事故率对p求导为:
(13)
4.1.1.2 一辆车通过路段的行程时间
由公式(5)可知,一辆车通过路段的行程时间t对自动驾驶汽车所占比p求导为:
(14)
4.1.2 求解U型曲线路段最优p值
所求结果如表1所示。
4.2 求解上升趋势路段最优自动驾驶汽车所占比
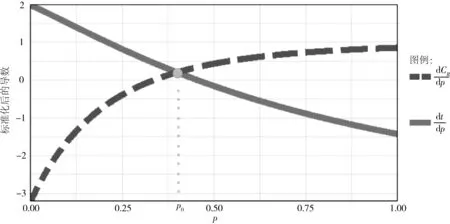
对于上升趋势道路,通过第2节与第3节的结论可知,随着自动驾驶汽车所占比p的变化,一辆车通过路段的行程时间t和事故率CR的变化速度有所不同;当p较小时,一辆车通过路段的行程时间t的减少速度比事故率CR的增加速度快。若t的减少速度与CR的增加速度相同时,有p=p0,则当p 表1 U型曲线路段的较优自动驾驶汽车所占比 4.2.1 构建上升趋势路段最优p值求解模型 (15) 其中,x为标准化前数据,x*为标准化后数据,xm为x的均值,σ为x的标准差。 4.2.2 求解上升趋势路段最优p值 图5 标准化后的与函数图像 由图5可知,路段1自动驾驶汽车的最优占有比率p0为40%左右,此时该路段的事故率与车辆通过路段的行程时间达到一个较为平衡的状态,一定程度上减缓了交通压力。 通过上述模型,对各个路段的较优自动汽车所占比、通行时间、事故率进行求解,结果如表2所示。 基于上述模型求解结果,分析各路段最优p值和事故率分布情况,以检验所确定p值的合理性,并给出了设立自动驾驶汽车专用车道的条件,为自动驾驶汽车的实际应用提供理论支撑。 表2 上升趋势路段的较优自动驾驶汽车所占比 首先分析自动驾驶汽车较优所占比p的分布情况,绘制其分布图。其次在实现较优自动驾驶汽车所占比p条件下,对道路的事故率进行分析,绘制事故率CR的分布图,如图6所示。 图6 较优所占比及事故率分布图 由图6可知,这两个分布图的趋势均呈现M型,存在两个极值点。最优自动驾驶汽车所占比p的分布存在两个极大值点,分别为p=0.1和p=0.4。在实现较优自动驾驶汽车所占比条件下,路段事故率CR的分布存在两个极大值点,分别为CR=35和CR=100,一个极小值点为CR=75。 根据图6中较优自动驾驶汽车所占比p的极大值点分布情况,可将路段分为两类,分别适合自动驾驶汽车所占比p=0.1和p=0.4。经检验,在实现较优自动驾驶汽车所占比的情况下,路段每百万公里的事故率均为30~50次,车辆行程时间均在1.5~1.8 min,结果处于理想范围之内。而对于个别在较优自动驾驶汽车所占比的情况下事故率仍然过高的路段,应采取相应措施,比如开辟自动驾驶汽车专用车道[17-18],以此增加出行效率,同时减少车辆间交互行为。 由图6中事故率CR的分布情况,结合事故率CR的理想范围为[0,92.47][19],建议在实现最优p值条件下,对于事故率CR>92.47的路段应开设自动驾驶汽车专用车道。通过RStudio软件进行数据筛选,得出需要开辟专用车道的路段,如表3所示。 表3 需要设专用车道的路段表 综上所述,本文利用美国华盛顿州Thurston、Pierce和Snohomish等地的路段起点、路段终点、平均每日车流量、道路匝数等数据(2017 MCM数据),基于BPR改进函数和V/C比,以自动驾驶汽车所占比为变量,从出行效率和安全两方面考虑,预测并分析自动驾驶汽车实际应用的行程时间和事故率情况。通过建立、求解路段行程时间模型及V/C比与事故率关系模型可得:自动驾驶汽车所占比增加,路段行程时间减少,路段事故率呈增加趋势或U型趋势。针对不同路段,综合考虑确定一个较优的自动驾驶汽车所占比。除此之外,在此基础上对模型鲁棒性及所确定的p值进行检验,发现大部分路段在实现较优自动驾驶汽车所占比的条件下,车辆行程时间及事故率均处于理想范围之内。对于小部分事故率仍然较高的路段,给出了设立自动驾驶汽车专用车道条件。 本文研究成果可以为自动驾驶汽车投入实际应用提供理论支撑和决策依据。但由于缺少自动驾驶汽车投入使用后的相关数据,无法全面考虑自动驾驶汽车投入后所带来的影响。在自动驾驶汽车投入实际应用后,应基于实际的路段行程时间和事故率等数据对行程时间函数和事故率函数进行拟合,得到的模型将更加符合实际路况,这也是我们下一步研究的方向。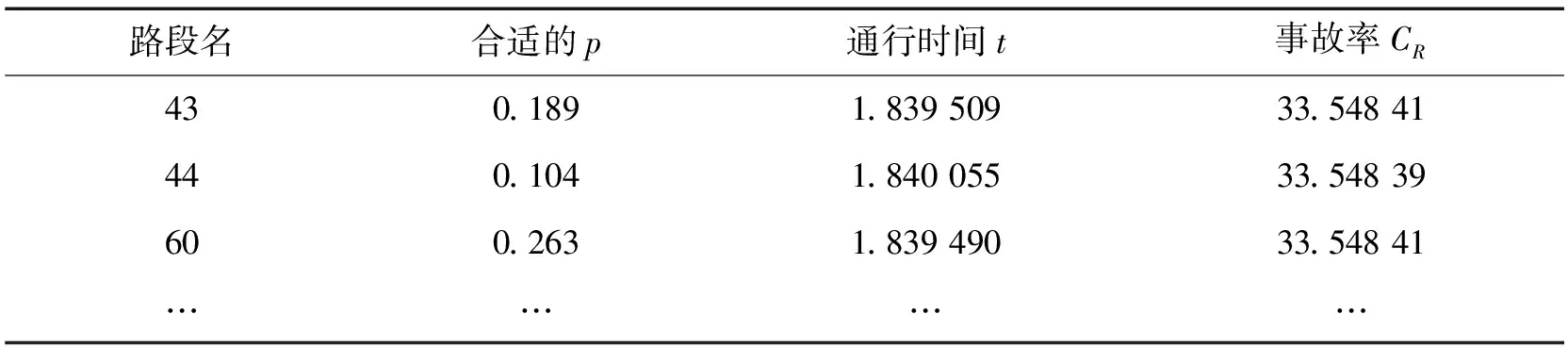
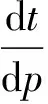
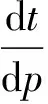
5 实证分析

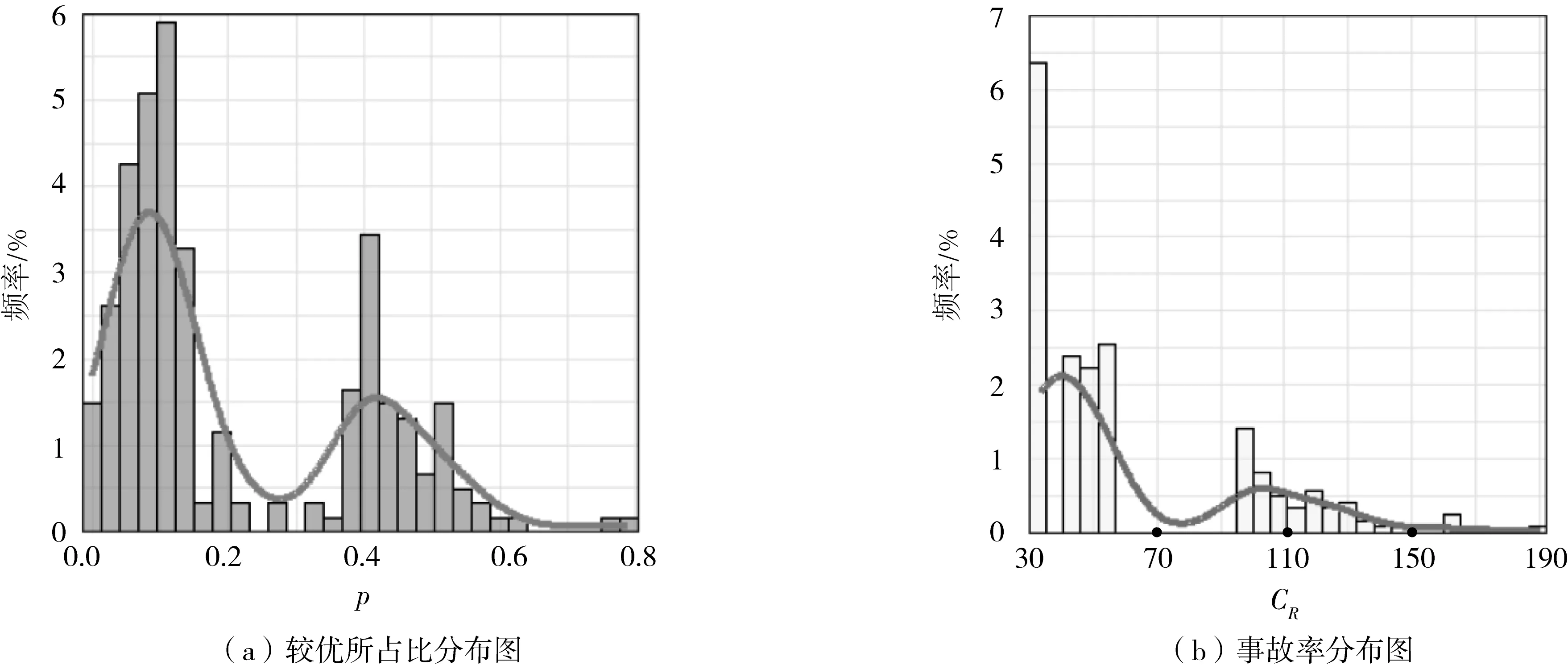
5.1 参数p和CR的分布情况
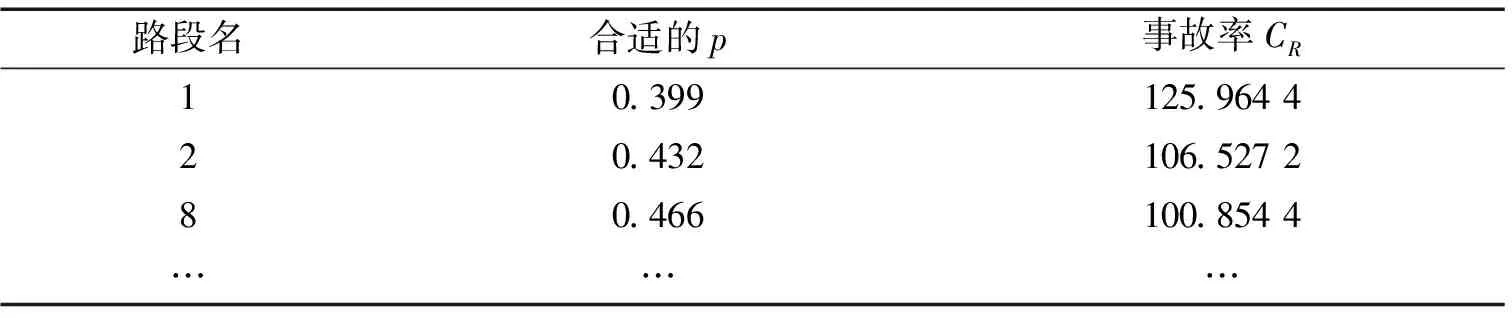
5.2 实施建议
6 结语
