An Improved Consensus Model Based on Multiple Attribute Consensus Rule with Minimum Adjustment
2019-10-24LIJianming
LI Jianming
(School of Mathematics and Statistics, Guizhou University, Guiyang 550025, China)
Abstract: For group decision making problems, consensus reaching process is usually an interactive and iterative process depicted as a consensus model or algorithm. During solving the multiple attribute group decision making( MAGDM) problems, consensus models based on multiple attribute consensus rules with minimum adjustments have attracted more attention recently. In this paper, an example is given to illustrate that the convergence of the existing consensus model cannot be guaranteed because of the defect in its preference adjustment suggestions(There is an error in the proof of its convergence of the existing consensus model).Then an improved consensus model is proposed and the convergence of the algorithm is proved and the example shows that the effectiveness and the wider applicability of the improved consensus model. The preference adjustment method proposed in this paper may be useful as a reference to improve other related consensus models (or consensus algorithms)and develop new consensus models with minimum adjustments for MAGDM problems.
Key words:multiple attribute group decision making; consensus reaching process; minimum adjustments; multiple attribute consensus rules; preference adjustment method; consensus model; convergence
The theory and methods of group decision making (GDM) have been widely applied to politics, economics, management and other areas. For a GDM problem, with different professional backgrounds and interest appeals, decision makers (or experts) have different opinions on the same decision problem, thus to get a solution with full and unanimous consensus is usually unreachable. In most cases, some extent of opinion consistence is acceptable. Here, to reach a consensus for GDM problems means to get a collective solution with the acceptable consensus level. The consensus level (or consensus degree) measures the opinion similarity of all the experts in the group. A consensus reaching process for GDM problems is often designed as a consensus model (or consensus algorithm) with which the group consensus can be attained. Research on consensus is an important area of GDM[1~14].
For decision problems, we often need more than one criterion (or attribute) to evaluate the alternatives. Naturally, consensus reaching processes for multiple attribute group decision making (MAGDM) problems have caught the attentions of many scholars[1-2,4-5,11,13-14]. A consensus reaching process should follow certain consensus rule. Based on the concept of minimum-cost consensus proposed by BEN-ARIEH et al.[3], ZHANG et al.[1]proposed two multiple attribute consensus rules with minimum adjustment named as Consensus rule 1 and Consensus rule 2, which are respectively called as distance-based consensus rule and count-based consensus rule in [2]. And with these two consensus rules, ZHANG et al.[1]developed novel consensus models for consensus reaching process in MAGDM. But the preference adjustment suggestions in these models may lead to no convergence in the interactive and iterative processes. And the convergence of consensus reaching process is the guarantee of reaching the group consensus. The main work of this paper has two aspects. One is that we construct an example to show the convergence defects for Consensus model 1 of [1]. The other is that we propose an improved consensus model and have proved its convergence.
This paper is organized as following. In section 1, some basic concepts related to consensus process for MAGDM problems are presented, and Consensus rule 1 is introduced which is a multiple attribute consensus rule with minimum adjustments. In section 2, we first introduce Consensus model 1 of [1]. Then we construct an example to show that the convergence of Consensus mode l cannot be guaranteed. In section 3, based on Consensus rule 1, we propose an improved model and give the proof of the corresponding convergent theorem. In the last, a brief conclusion is presented in section 4.
1 Concepts on consensus process for MAGDM problems
1.1 MAGDM problem
LetX={x1,x2,…,xm}be a set of alternatives.


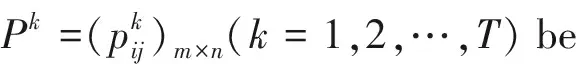
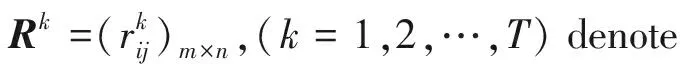

If we use the OWA operator, then

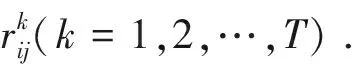
(1)
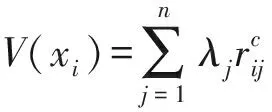
1.2 Consensus measure
For above MAGMD problems, to measure the similarity (or consistence) of the expert opinions, consensus measure is introduced. There are several ways to define consensus measure. Based on the definition of decision matrix similarity degree in [4], ZHANG et al.[1]introduce the following definition.

(2)
Obviously, when the value of consensus measure is smaller, the group consensus degree is higher.
1.3 Consensus rule
Consensus rule points out the general direction of consensus reaching process. In the consensus reaching process, in order to get a higher level of group consensus degree, we need to design a feedback mechanism to guide the experts to modify their opinions.A feedback mechanism is designed based on certain consensus rule.In the following, we introduce Consensus rule 1 in [1], which is a multiple attribute consensus rule with minimum adjustments.The Consensus rule 1 is also called distance-based consensus rule in [2].The idea of Consensus rule 1 is similar to that of searching local ideal points by using a mathematical programming.
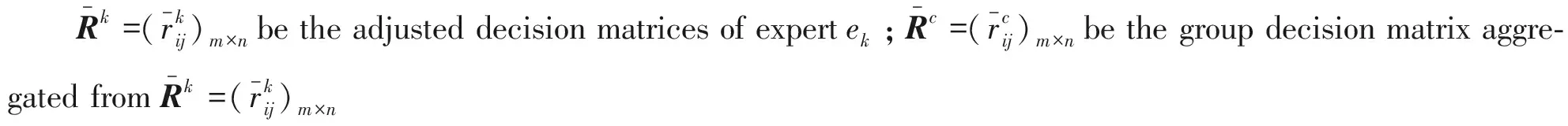
Consensusrule1

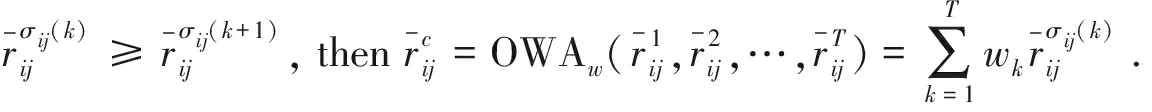
Following theorem comes directly from paper [1].


2 A counter example to the convergence of Consensus model 1 in [1]
In the following,we first introduce Consensus model 1 proposed in [1]. Then we construct an example to show that the convergence of Consensus model 1 cannot be guaranteed.
Consensusmodel1(presented in [1], or named as Algorithm 6.1 in [2]).
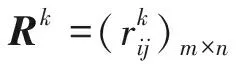






Applying Consensus model 1 to Example 1, we have that:
w=(0.5, 0.5)T.

From Step 2 of Consensus model 1,

By usingP2, we have




=…

=0.2(1-3-(l+1)), (l=0,1,2,…).
(3)


=…

=1-0.2(1-3-(l+1)), (l=0,1,2,…).
(4)

=0.5-0.2(1-3-l)
>0.3>α=0.1, (l=1,2,3,…).
(5)

=0.2(1+3-l);
therefore,
Dl=0.4(1+3-l)>0.4, (l=0,1,2,…).
(6)
When the experts modify their preferences (or opinions) according to expressions (3) and (4), the expression (5) shows that Step 4 of Consensus model 1 will never be arrived. Therefore, applying Consensus model 1 to Example 1, the iterative process is not convergent. So the group consensus cannot be reached.


3 The improved consensus model and its convergence
In order to guarantee the convergence of consensus process, we propose following improved consensus model based on Consensus rule 1.
Consensusmodel2






Next, we will prove the convergence of Consensus model 2. Following Lemma 3.1 is similar to Lemma 4.1 of [1]. So we omit its proof.


That is,∀ε>0, ∃N>0, whenl≥N, we have|Dl-Dl+1|<ε.
Again from Lemma 4.1 of [1], we have that
(7)


Theorem3.1Letαbe the given consensus threshold, and
ProofFrom Lemma 3.2,
(8)

(9)
From (8) and (9), we have that
(10)
From Consensus rule 1(i.e.,P1), we have that
(11)
Obviously,


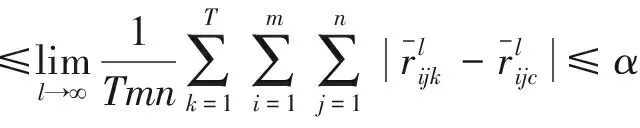



4 Conclusions
With Example 1, Remark 2.1 points out that the mistakes of convergent proof in Consensus model 1; and Remark 2.2 points out the defect of preference adjustment suggestion in Consensus model 1; the preference adjustment suggestion also appears in other consensus models of [1]whose contents had been collected as the last part of book [2]. The convergence of Consensus model 2 proposed in this paper have been proved. And Example 2 shows the validity of Consensus model 2. The preference adjustment method of Consensus model 2 may be useful as a reference to improve and develop other related consensus models with minimum adjustments for MAGDM problems.
AcknowledgmentsThe author thanks the reviewers for their suggestions to polish this paper.
