基于改进光流场算法在复杂背景变化图像处理中的应用

许 磊,戚 睿,袁 杰,刘 研,温乃峰

(1.哈尔滨工业大学 计算机科学与技术学院,黑龙江 哈尔滨 150001;2.海南职业技术学院,海南 海口 570100;3.上海航天电子技术研究所,上海 201109;4.哈尔滨工业大学 数学学院,黑龙江 哈尔滨 150001;5.大连民族大学 机电工程学院,辽宁 大连 116600)

0 引言

随着计算机科学技术的发展,图像和视频的智能处理被应用在越来越多的领域中[1]。由于目标定位与跟踪技术的广泛应用,计算机对不同领域图像处理的要求也随之增加[2]。图像配准技术可根据追踪目标在图像序列之间的特征变化,同时获取目标在不同时间点内位置空间和自身形状的变化信息[3]。在目标跟踪领域,图像配准可用于减小因拍摄设备的颤动而引起不同帧在相关位置上产生的误差,以及获取目标在不同帧之间的形变信息[4]。经过国内外学者长期的研究,图像配准技术已在很多领域中的目标跟踪应用中起到了关键的作用[5]。目前对于图像配准技术已日趋成熟,有着较为完整的体系和框架,主要分为刚性配准方法和非刚性配准方法[6-8]。其中,刚性配准采用基于旋转和平移的自由度变换,将参考图像的对应点映射到浮动图像的对应点。在一些领域中,具有复杂结构图像的目标位置以及自身结构存在变化,导致刚性图像配准在处理复杂结构图像时具有一定的局限性,故只能处理刚体图像[9]。非刚性配准可提取图像中的不同特征,同时反映图像的空间和形变信息[10],因此,非刚性配准方法为当今目标跟踪领域中的一个研究热点。

现有基于非刚性的图像配准算法可分为两类：基于特征的算法和基于像素点的算法。基于上述2种算法,已经开发了不同图像的配准方法[11-13]。然而,这些方法在处理复杂背景变化的图像序列时仍存在问题。基于特征的算法对于通过将变形图像中的几何特征和局部纹理特征等与静态图像中的相同特征相匹配来处理噪声图像是有用的。然而,由于图像结构变化的应力会引起损伤位置、形状、大小和纹理变化,特征提取的潜在误差可被延续到可变形图像配准过程中。此外,需要额外的时间来完成特征提取环节。基于灰度的算法可直接使用像素(或体素)信息,但基于灰度的算法(如基于平方强度差之和SSD和绝对差之和SAD的配准方法对少量像素非常敏感)在图像之间具有非常大的灰度差异,例如噪声[13-14]。虽然有些方法使用平滑操作可以抑制配准过程中的噪声[15],但权衡噪声和特征为一种两难选择。因此,需要开发一种对复杂背景变化图像具有稳健性的非刚性图像配准方法。

由于线性计算具有复杂性且易于实现,Demons算法是非刚性图像配准的流行算法[16]。本文提出了一种基于Demons算法的全自动非刚性图像配准方法,用于对于复杂结构图像的处理。为处理图像低信噪比,将基于“牛顿第一定律运动”的思想集成为一种新的驱动力并融入原始基于Demons力的光流场公式中,在图像空间中任何一点处的Demons力将产生源自在Moore邻里系统中局灰度变化趋势的“惯性”力。

1 本文思路

基于传统的“Demons”算法使用静态图像中像素的局部梯度信息来驱动运动图像中的像素扩散到相应的静态图像中。在原始Demons算法中,采用光流方程用于估计Demons力。对于给定点p,设静态图像S中的给定点的特征值为S(p),M(p)为运动图像M中的给定点的特征值。基于上述定义,匹配图像中对应点所需的估计位移可表示为

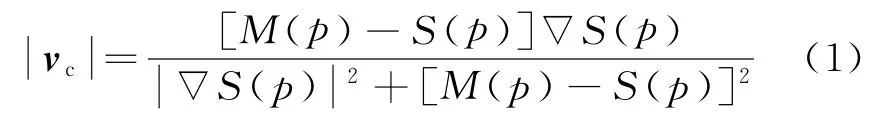
式中：vc=(v i,v j),i,j为图像S和M中给定像素点的坐标位置;∇S(p)是静态图像中像素点的局部梯度信息,表示“内力”,用来计算静态图像中的相邻像素的关系;M(p)-S(p)表示静态图像和动态图像之间的差异相互作用的“外部”力。Demons算法工作原理如图1所示。由图可知,在原始的Demons算法中,像素的位移将根据Demons力按照∇S(p)的方向(当S(p)＜M(p)时)推动像素点,或者沿着-∇S(p)的方向拉动像素点(当S(p)＞M(p)∇S时)。

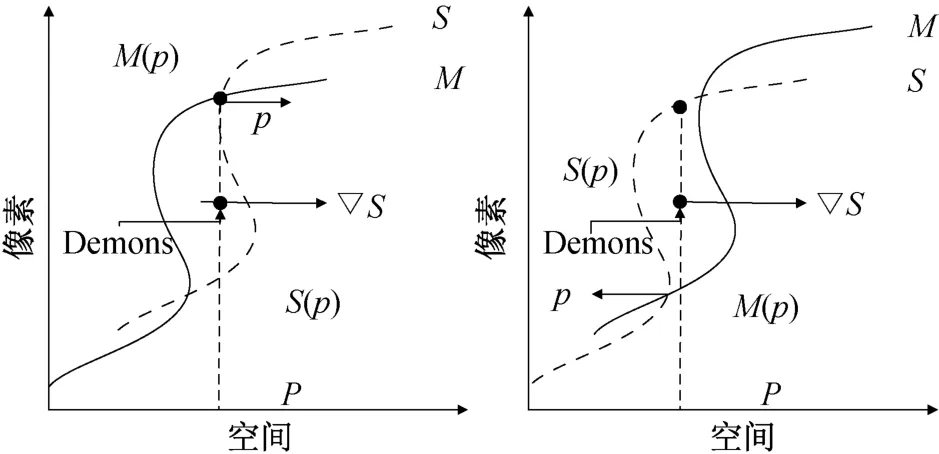
图1 Demons算法工作原理Fig.1 Working principle of Demons algorithm

式(1)以迭代的方式计算估计Demons力,直到Demons收敛到稳定的状态。然而,由于驱动变形的原始Demons力仅取自静态图像空间中每个像素的梯度,故当噪声或复杂背景变化引起的像素点变化趋势严重不稳定时,静态图像中的局部梯度信息会变得不稳定,从而使基于原始Demons算法在处理带有复杂背景变化图像时可能发生错误。Demons在处理复杂图像时的情况如图2所示。

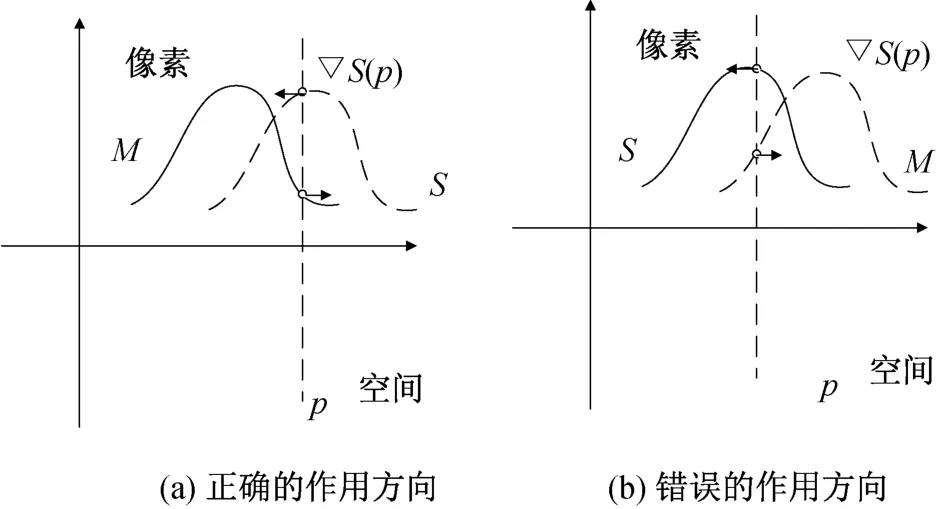
图2 Demons在处理复杂图像时的情况Fig.2 Demons in dealing with complex images

图2(a)中,利用原始的Demons力,将标记的移动像素M(p)的位置与静态图像中的对应点较好地匹配。对图2(b)中的标记移动像素施加相同的力。由图2(b)可知,由于不稳定的梯度信息,标记的像素M(p)被移动到不合适的位置。此外,由于仅根据局部图像信息计算移动像素的位移,故基本上需要平滑操作来抑制噪声,以保持变形图像的几何连续性。

基于原始Demons算法,在每次迭代过程中,光流方程需伴随使用带有方差σ2的高斯滤波器对变形场进行正则化。但如果σ设置太小,则抑制噪声的效率会变得低下。如果σ设置太大,则对于图像细节的保留可能会大大降低。一些研究通过在光流方程中加入不同类型的额外力来估计Demons力[15,17],但这些方法在处理图像的低信噪比时仍存在问题,当对局部信息进行梯度运算时,配准过程也可能发生效率低下的情况,即在静态图像和运动图像中都是不稳定的。

牛顿的第一定律是构成经典力学基础的最强大的物理定律,它描述了作用于物体的力与由于这些力而产生的运动之间的关系。根据牛顿第一定律：处于均匀运动状态的每个物体都倾向于保持该运动状态,除非对其施加外力。假设移动物体遇到障碍物,它可能不会被障碍物的阻力阻挡,而是通过其“惯性”保持其原始速度方向。类似地,在图像运动场景中,运动图像空间中的像素被视为由静态图像的局部梯度信息导出的“内力”驱动的运动对象。静态图像中的斑点噪声被视为障碍物,由于像素点灰度的严重不规则变化而给予移动物体阻力。为帮助移动物体更有效地扩散到相应的静态物体中,本文将基于“牛顿第一定律运动”的新“惯性力”添加到原始的光流场方程中,从而将Demons力重新定义为

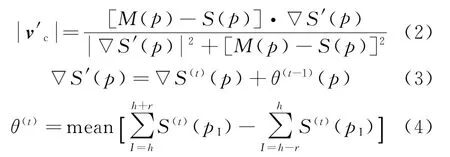
式中：h为点p在(i,j)处的灰度值,h±r为(i,j±r)或(i±r,j)处的灰度值,其中r为邻域半径;t为迭代次数;θ(p)是一种“惯性”力,来源于半径大小r=3的Moore邻域系统中邻近像素的全局强度趋势。式(2)中,M(p)-S(p)是用于强调M(p)偏移的“外部”力,∇S'(p)是用于强调由原始内力S(p)和“惯性”力θ(p)集成的移动M(p)的新“内部”力。假设∇S(t)(p)是驱动运动物体M(p)在第t次迭代时上扩散到静态图像中的对应点的力,θ(p)为每个像素M(p)以迭代的方式提供的额外力,以驱动该像素移动到期望方向。如果“惯性”力θ(p)与原始内力具有相同的动作方向,根据牛顿第一定律,v将保持恒定。如果原始内力与惯性力具有相反的作用方向,则在几次迭代之后,v方向将逐渐被惯性力修改,最后固定运动物体的位移,如图3所示。

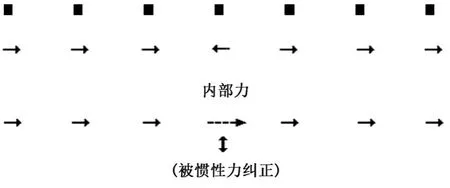
图3 本文方法对像素点的引导作用Fig.3 Guiding effect of the proposed method on pixels

2 评估方法

为评估配准结果的性能,使用3个相似性度量函数：平方差和(sum of squared difference,SSD)、相关系数(correlation coefficient,CC)和归一化互信息(normalized mutual information,MI_N)来统计评估本文算法。SSD是通过在静态图像和变形图像之间的平方邻域内减去像素强度而计算的最普遍的相似性度量之一。设S为变形图像的像素集,D为相应静态图像的像素集,则SSD定义为

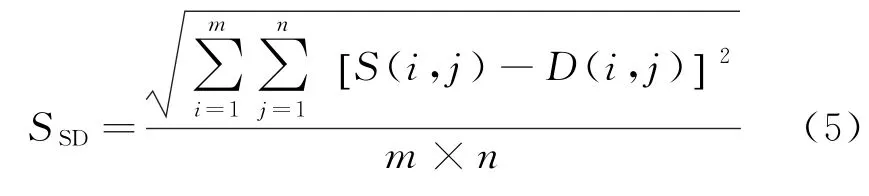
当SSD比率较低时,变形图像更类似于相应的静态图像。相关系数(CC)用于统计分析测量2个相应图像匹配程度的线性相关性,描述了在不同时间获取的2个图像之间的重叠区域的延伸。如果2个图像完全相同,则相关系数值CC=1,即配准结果表现最好。如果2个图像完全不相关,则CC=0。CC定义为

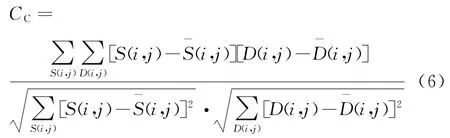
互信息可定性地衡量一个图像与另一个图像的匹配程度。通过配准2个图像之间的灰度分布的联合直方图来计算互信息。互信息定义为

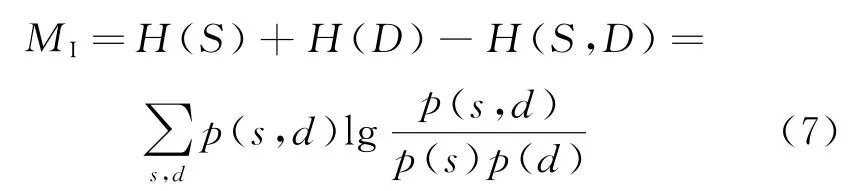
式中：p(s)为图像S的熵;p(d)为图像D的熵;p(s,d)是图像S和图像D的联合熵。为便于数据统计,采用归一化互信息MI_N来评估本文算法。

3 实验结果

为评估本文提出的Demons扩散模型的效果,首先将该方法应用于航拍的具有复杂结构图像的配准中,并和基于原始Demons的配准方法进行对比。实验结果如图4所示。图4(a)是在初始时从航拍视频捕获的原始图像,图4(b)是在0.5 s后从相同视频捕获的对应运动图像。通过使用原始Demons模型,在图4(c)中生成配准结果。

由图4(c)可知,结果中产生了许多马赛克状的斑点区域,配准结果显得非常不平滑。原始Demons模型得到的结果很差,这是由于原始Demons模型的估计Demons力来自单独像素的局部梯度信息。如图3所示,图像自然场景等复杂背景变化所产生的噪声,混淆了移动物体的移动方向,这是因为相应点与左右相邻像素之间的灰度变化趋势均相同。在这种情况下,移动的对象可能被驱动到相对方向相应的静态对象,导致产生琐碎区域或马赛克现象,最终得到效果较差的配准结果。

图4 两种方法的配准结果Fig.4 The registration results of two methods

使用本文方法生成的配准结果如图4(d)所示。与图4(c)相比,本文方法的配准结果显得更加平滑,同时保留了原始图像的细节和变形图像的几何连续性。该方法产生较好的结果如下：1)利用惯性力,可根据迭代过程中的全局灰度趋势,确定由斑点噪声点局部梯度信息得到的非定常力;因此,所提出的方法对噪声不敏感。2)所提方法中,没有采用任何平滑操作来抑制噪声,故可很好地保留图像的细节。3)由于在图像空间中任意一点处Demons力都被局部图像信息和全局强度趋势信息整合在一起,因此图像的几何连续性也可得到保留。

为统计性地验证本文方法的配准性能,对于每个实例,本文分别计算静态图像与其对应的运动图像(SSDsm)之间的SSD以及通过使用不同方法生成的静态图像和对应的变形图像(SSDdm)之间的SSD值。采用归一化为1 的阈值作为相似性标准,即通过PSD=SSDsd/SSDsm表示SSDsm和SSDdm之间的相似关系。PSD＜1表示变形图像和静态图像比运动图像更相似,且意味着配准是有效的。

对于数据库中的图像,原始光流场方法和本文方法的PSD平均值分别为1.02和0.57。由此可见,传统方法对于数据集中的所有图像PSD统计均值大于1,说明采用原始配准方法得到的结果和浮动图像对比而言偏离度较大。相对于传统的光流场方法,本文方法有着更低的PSD值,说明本文方法的配准结果更加有效。为评估不同方法的整体性能,本实验将基于原始光流场的配准模型和本文方法应用于实验数据集。表1列出3种方法的相似性度量指标,从表1中可看出本文方法的SSD较低,而CC和MI_N高于原始光流场方法。这表明本文所提方法的配准结果更准确。

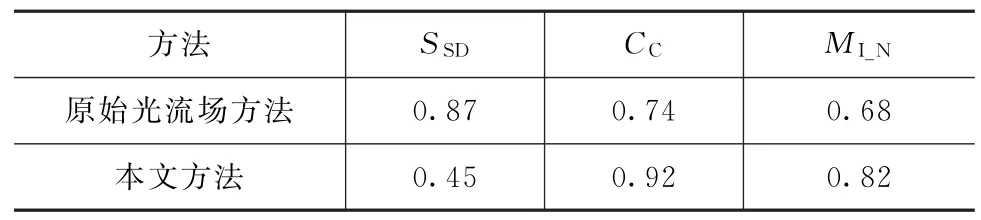
表1 两种方法的3种评价指标对比Tab.1 Comparison of three evaluation indicators of two methods

本文还对2种方法的处理速度进行了测试。测试基于MATLAB编程语言,在CPU 为4核、内存为4G RAM 的计算机上执行。因执行可变形图像配准的计算时间取决于图像的大小以及运动图像相对于对应参考图像的相似性,对于一幅240 pixel×400 pixel的图像来说,基于原始光流场的方法需要约20 s才能完成处理。相对于基于原始光流场的方法,本文方法仅需更少的时间即可达到收敛(约10 s),这是因为本文方法在每次迭代过程中未使用任何平滑操作来抑制噪声。

4 结论

通过改进Demons算法,实现了一种有效的用于具有复杂结构图像的可变形图像配准技术。为处理低信噪比,本文方法基于牛顿第一定律为光流方程增加了新的力,以更加有效地驱动运动图像中的像素扩散到相应的参考图像对象中。与其他基于Demons算法的配准方法相比,该方法可有效、自动地配准图像,且对噪声具有稳健性。