新课改视阈下初高中数学的衔接问题研究
2019-10-23肖钦欢邱克娥陈娜陈莎潘彬彬杨艳珍
肖钦欢 邱克娥 陈娜 陈莎 潘彬彬 杨艳珍
(贵州师范学院 数学与大数据学院,贵州 贵阳 550018)
随着我国新课程改革的全面普及,初高中数学的差异越发明显。无论是在学科内容,还是在学习方法等方面都有重大改变。初中数学属于义务教育,高中数学则属于基础教育,是为接受高等教育打下基础。义务教育具有普及性,所以教材难度较低、学科知识较为简单,知识点分类明确;而基础教育承担着为高等院校输送人才的基本任务,面临高考选拔,具有优选性质[1]。高中教材对比初中,显得内容繁多、难度大幅度提升,知识点分类不再明显,多是融为一体,如初中的图形与几何、数与代数是分开的,但到了高中,都归为了几何与代数一类。由于教材内容安排的改变,初中的学习方法不再适用,致使学生进入新的环境后,数学成绩大幅度下滑,初中数学成绩好的,到高中后甚至连及格都难保证[2]。这一方面是教材难度加大的原因,另一方面也是存在初高中知识衔接不当的关系。下面,从初中教学出发,结合课题组成员的教学经验,在新课改的背景下,以人教版为例,提供数与代数、图形与几何、统计与概率这三大方面的一些具体衔接教学措施,供大家探讨参考。
以2018年贵阳市中考题第18题为例,如图1,在Rt△ABC中,下面为小亮探究之间关系的方法:

联系自己所学的三角函数知识,在图2的锐角△ABC中,思考三者之间的关系,并写出探究过程。

图1

图2
显而易见,这道题答案就是高中的正弦定理推导过程的一部分,因此,若在处理初高中衔接问题中,从初中数学的教学出发,在具体教学过程中,补充一些与高中知识接轨的内容,既能让学生在接触到高中知识时不再一无所知,也解决了遇到类似中考题时没有思路的困境,毕竟初中到高中过渡的过程,以初中教师的角度来看,就是一个补充扩展的过程,但以高中教师的角度则是一个回顾联系的过程。
一、数与代数
以y=x2-2x-3和y=-x2-4x-3为例,结合它们函数图像,可以发现a和x范围确定时,y的变化情况。
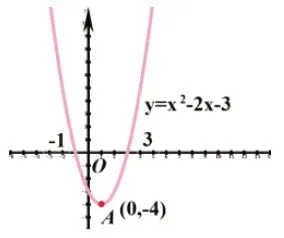
图3
如图3,x>1时,x增大y也增大,x<1时,x增大y减小。

图4
如图4,x>-2时,x增大y减小,x<-2时,x增大y也增大。
这里虽讨论了x范围确定时y的变化情况,但并没考虑,若y的范围确定时x的取值范围又是多少?比如函数y=x2-2x-3,当y<0,y<5时,x的取值范围是多少?根据函数图像知:y<0时,x的取值范围为-1<x<3,即x2-2x-3<0这个不等式的解集为-1<x<3;y<5时,x的取值范围为-2<x<4,即x2-2x-3<5的解集为-2<x<4。这就和高中的一元二次不等式相联系[3]。虽没给出一元二次不等式的定义,但可根据二次函数的图像解决此类不等式解的问题,所以在讲这节知识点时,不妨将这种情况一起讲了,在讲解中,可以引导学生反向思考,从而推出求x的取值范围,既保证了初高中知识的衔接,也使学生养成了勤于思考的习惯,为以后高中的学习奠定了良好基础。
例:(黔南州中考)如图5,已知抛物线y=x2+bx+c的图象与y轴交于点C(0,-6),与x轴的一个交点A(-2,0)。
(1)求此抛物线的表达式,并把定点D的坐标写出来;

图5
问题(2)就是一个根据图象解决一元二次不等式的例子,若老师讲二次函数时,就讲了这种例子,学生在遇到类似的题就不会束手无策了,也为接触高中知识中一元二次不等式时打下基础。
二、图形与几何
对于圆的定义,初中是利用点动成线,线动成面的思想,定义圆为平面内一线段绕固定一端点旋转一周所形成的图形;而高中是利用集合的思想,定义圆为到定点距离是定长的点的集合。这就将图形与几何和代数联系起来了,并由此结合距离公式推导出了圆的标准方程为(x-a)2+(y-b)2=r2,其中定点(a,b),定长r。这就从方程的角度来描述圆,也体现了数形结合的思想[3]。但在高中生初次接触到圆的方程时,总有同学想去解,但自己又不会解,因为初中只学过二元一次方程和一元二次方程,高中也没讲二元二次方程的求解,所以这就是一个初高中衔接不当的地方。
现从初中老师的角度出发,给学生讲用配方法求解一元二次方程时,可以插入特殊二元二次方程的求解,如x2+y2-10x-12y+61=0,可用配方法配成两个完全平方式(x-5)2+(y-6)2=0,解得x=5,y=6。由此扩展,r>0时,二元二次方程有多少组解呢?比如(x-5)2+(y-6)2=16,利用换元的思想,将x-5和y-6分别用m和n替换掉,原方程就变为了m2+n2+16,再化简为由平方根根号内的数必须大于或等于零,解得n取值范围为-4≤n≤4,同理得m取值范围为-4≤m≤4,从数轴看-4到4间有无穷个数,所以二元二次方程有无穷组解,就和二元一次方程有无穷组解原理相同。这也对应了高中圆的方程有无穷解,即圆上的点也有无穷个。所以圆的方程不用求解,学生只需判断点是在圆上(即点满足方程(x1-a)2-(y1-b)2=r2),在圆内((x2-a)2-(y2-b)2=r2)还是圆外((x3-a)2-(y3-b)2=r2),如图6。
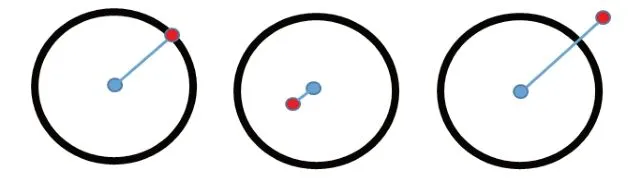
图6
三、统计与概率
初中对概率的定义是刻画随机事件发生可能性大小的数值,而高中对概率的定义是度量随机事件发生的可能性大小,二者并无太大差别,但是高中有讲分类加法计数原理和分步乘法计数原理,而初中计算概率的方法只有列举法,分别为列表法和树状图。
然而,树状图与列表法都是计算事件发生可能性次数的方法,但有些实际问题计算概率就不能单纯的用树状图与列表法来计算。例如甲、乙两人进行乒乓球比赛,比赛规则为3局2胜制,如果两人在每局比赛中获胜的概率都相等,在比赛开始后,甲先胜了第1局,最后甲获胜的概率是多少?如果用树状图来解决,就如图7但是若按照个数来看,获胜概率为,但利用公式法(即通过分类加法、分步乘法计数原理)可得P(甲胜)。这道题的答案是 ,所以树状图不能处理此类问题,这是树状图实际应用的缺陷,当然,若按照理论计算,树状图没有问题,即假设一定完成3场比赛,利用树状图就可以得到,如图8

图7

图8
如果我们在初中概率就插入简单的分类加法计数原理和分步乘法计数原理,那么学生就更能理解清楚概率的概念。从而学生会列公式计算概率,更加节约计算时间,减小计算量,而且也为高中接触排列组合打下基础。
四、结束语
数学在学生的学习生涯中扮演着无法替代的角色,初高中数学的学习尤为重要,它们之间的衔接问题的研究也成为一大难题,就目前来看,并没有统一的研究方法。而本文主要致力于数与代数、图形与几何、统计与概率三方面内容衔接问题进行研究,找到该类型问题的一般性解决思路和方法,比以往解决问题的方式更加高效,在促进初高中数学知识正迁移的同时,实现了初中和高中数学教学的无缝衔接。
