基于Taylor二阶展开的双线性插值偏角足迹校正技术
2019-10-23樊少勇黄晓春
包 清, 樊少勇, 黄晓春
(1.上海市公安局刑事侦查总队, 上海 200083; 2.上海理工大学, 上海 200093)
0 引言
传统物证摄影中,为保证痕迹物证不变形,相机镜头一般垂直于痕迹物证,允许的偏角不超过5°。但实际工作中,偏角摄影有着不可忽视的实用价值,主要体现在两种情况中:一是痕迹物证受到场景的制约,垂直拍摄存在困难甚至无法完成;二是非光滑承痕体上的漫反射痕迹,光线与痕迹和承痕体作用后均表现为漫反射,在垂直方向上可能无法获得大反差图像,根据非Lambert光照反射模型,在大偏角处可能存在痕迹与承痕体反射能量反差最大的角度。第二种情况是传统的物证摄影理论中忽视的双漫反射情况,传统物证摄影理论的分析局限于光滑客体上的粗糙痕迹和粗糙客体上的光滑痕迹,对于痕迹和承痕体反射性质相近且均为漫反射的情况下的拍摄状况讨论和解释并不详尽[1]。在偏角拍摄中痕迹的变形是影响检验的重要因素,为使物证图像能够被应用于检验,对拍摄的变形图像进行修正变得至关重要[2-3]。本文找到了一种基于Taylor二阶展开的双线性插值图像校正技术,与其他方法相比主要的优势:一是采用了Taylor二阶展开算法,可修正透视畸变,校正效果好;二是采用的算法计算量小,仅需要计算2个参数;三是操作简便实用性强,拍照时只需沿着足迹中心线放置单个长标尺即可,适用于公安实战。
1 偏角摄影校正技术的现状
偏角摄影的校正可以分为两大类,一是利用光路可逆原理对变形校正的物理校正方法;二是利用图像处理技术对数字图像进行处理的计算机校正方法[4]。物理校正方法需要增加额外的设备,操作过程对人员手工操作水平要求高,校正效果受手工操作影响大[5-6]。基于上述原因,采用计算机图像处理技术的“软校正”方法处理偏角摄影引起的图像变形,是当前常用的方法。
偏角摄影校正的关键主要有两点,一是校正变形的模型算法;二是校正后的图像插值处理[7]。
经查阅相关的文献,主要的偏角校正方法有:基于控制角点的解析式透视变换算法[8],但该方法仅仅考虑了投影的影响而没有考虑光学透镜组的影响;利用棱镜的多目视图校正透视图像的方法,该方法需要多目立体视图才能达到较好的校正效果[9];基于消失点的空间定位校正方法,该方法依据光学透镜组对畸变的影响,利用了透视导致的平行线相交,通过逆变换把一组正交的消失线转变为平行线以达到校正的目的[10],但该方法需求解6个参数并使用最小二乘法求极值,方法复杂计算量大,并且需要网格线进行辅助;基于霍夫直线检测的透视变换算法,该方法是校正有明显文字行的文档类图像的常用方法,主要包括平移变换、仿射变换和刚体变换[11-12],但该方法鲁棒性差,其核心仿射变换是一个线性变换,图像改善效果有限;基于投影法的校正方法,利用在两个方向上不断进行小角度θ的旋转,依据投影值的改变,通过找到极值,判断两个方向上的倾斜角并修正,该方法思路简单,但计算量极大,尤其为了精度把θ的值控制得很小时[12];利用通用软件PHOTOSHOP的处理校正,需要放置包围痕迹物证的比例尺,并且需要垂直和偏角各拍摄一次,利用降低透明度后,在PHOTOSHOP内手工拉伸完成校正[8],该方法拍摄操作和准备工作相对复杂,处理过程完全依赖手工,主观因素大,文中只有标尺校正而没有物证校正的图片,描述与图片不符,说服力不足;使用偏角足迹校正软件的方法[13],该方法需要控制的参数和条件多,且当沿着足迹的宽度方向偏角达到60°时已明显变形,无法应用于检验。
经查阅相关的文献,主要的插值方法有邻近插值法、双线性插值法、三次插值法、等角插补法[12,14]。其中邻近插值法采用复制邻近点RGB值的方式进行插值,方法简单、速度快,但效果最差;双线性插值法把插值点对应到真实图像的最近相邻点,在3×3的小窗口内利用加权系数定比分点的方法计算出插值点的RGB值,该方法效果较好,过渡缓和且曲线不变形;三次插值法保证了插值点邻域的二阶导的一致性,该方法效果可达肉眼无法分辨程度,但该方法需要一个4×4的窗口,并且需要计算二阶导,计算量大;等角插补法算法最符合透视模型,插值效果好,但该方法需要计算出原图两个相邻像素点之间的光照向量,过程繁琐计算量大。
2 实验原理和步骤
2.1 实验原理
2.1.1 透视校正原理
直观观察可以发现,偏角摄影与垂直摄影最明显的区别是偏角摄影结果近大远小,平行线变成了相交直线。这种透视畸变产生于成像过程中对于焦平面的偏离,下面结合示意图1利用高斯近轴成像进行分析。

图1 光路成像示意图
当相机准确对焦时,透过光心的光线、平行于透镜的光线、通过焦点的光线汇聚于一点,同心光束汇聚性好,当透镜的焦距和成像的像距不变时,如示意图所示向远离透镜的方向移动物体,以透镜光心为坐标原点向右和向上为正方向建立坐标系,记两个焦点分别为(f,0),(-f,0),物体的高度为h,移动前距透镜L1,移动后距透镜L2(L2>L1),解析法可得通过光心的光线以及在像平面的直线l1,l2并求出交点。
(1)
(2)
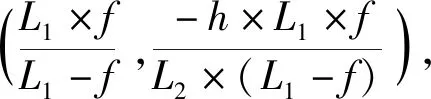
(3)
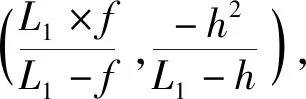
(4)
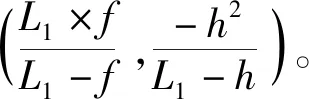
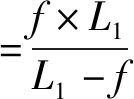
(5)
那么物体在像平面上的长度满足下式:
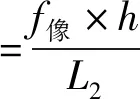
(6)
物体的放大率随着向透镜方向偏移而变大,向无穷远方向偏移而变小,这也是透视呈现出近大远小的原因。
若直接依据公式(6)通过逆变换校正变形图像,需要测得参数像距f像和待修正处的物距L2,操作可行性差,故对该式在L2处进行二阶Taylor展开
(7)
依据上式把偏移量x的一阶系数和二阶系数分别记为C、D,将公式(7)简化为公式(8)
(8)
依据公式(8)在焦平面附近的透视变形,可通过偏移量x的一阶和二阶增量的和近似代替,通过确定焦平面与被摄物体平面的交线,在水平和竖直方向上分别对图像进行非线性拉伸和压缩可达到消除偏离焦平面产生的畸变。
2.1.2 图像插值原理
双线性插值是一种运算比较简单效果比较良好的插值方法,在本文中插值过程如图2所示,为横向插值。
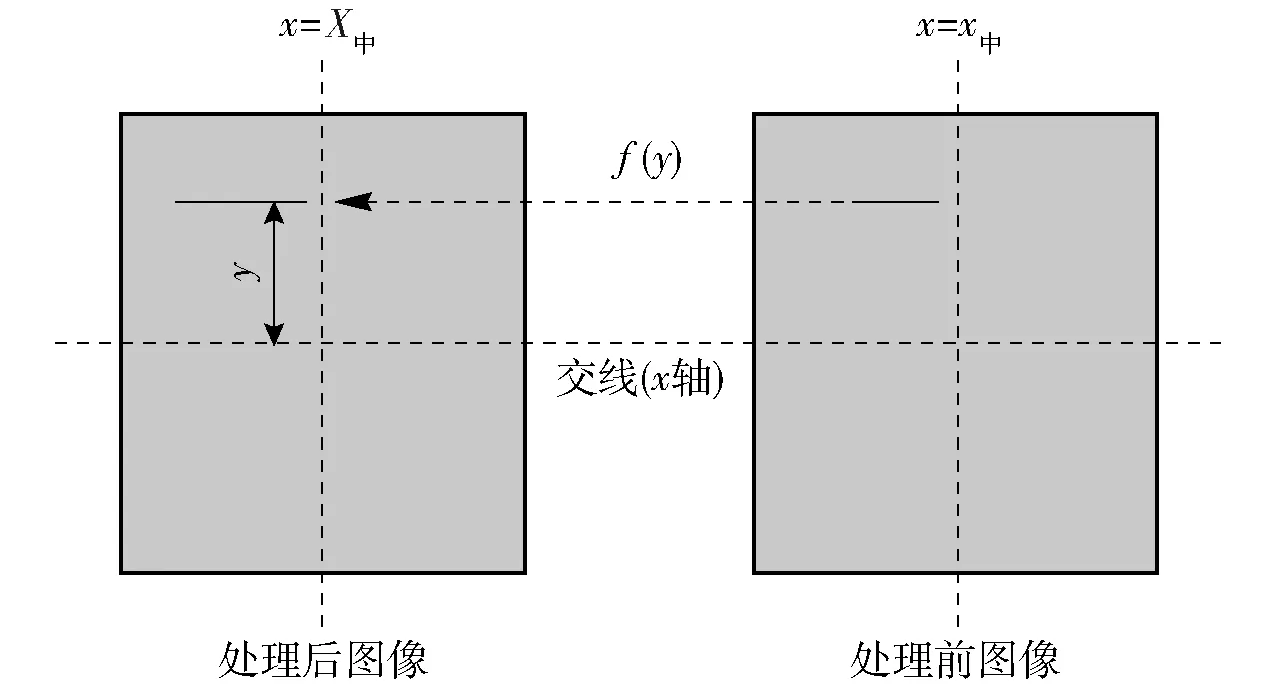
图2 横向插值示意图
记处理后图像中线的横坐标为X中,原始图像中线的横坐标为x中,所需要变换点的坐标为(i,j),原始图像变换对应点的横坐标为i原,变换的函数为f(y),是一个取决于点到交线距离y的函数,本文中是泰勒二阶展开的结果。图像上变换点到原始图像对应点的横坐标变换如公式(9)所示。
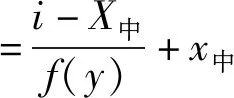
(9)
利用该虚拟点计算插值的方法如公式(10)、(11)、(12)所示,记floor(x)为向下取整函数,ceil(x)为向上取整函数,Pij为处理后该点的RGB值,pij为原始图像上一点的RGB值。
xs1=i原-floor(i原)
(10)
xs2=ceil(i原)-i原
(11)
Pij=xs1×pceil(i原)j+xs2×pfloor(i原)j
(12)
2.2 实验步骤
2.2.1 实验样本的制作与拍摄
对A4纸上的灰尘足迹,在足迹内侧平行足迹中心线方向加贴长度为30 cm宽度为2 cm的比例尺,采取垂直拍摄制作原样大小的样本,选取5个特征点分别标注为a、b、c、d、e,测得足迹全长和足迹宽度分别为,如图3所示。
使用佳能相机对该A4纸上的灰尘足迹进行偏角拍摄,采用自动对焦方式对画面中点进行对焦,拍摄角度分别为30°、45°、60°,如图4、图5、图6所示。

图3 垂直拍摄

图4 30°偏角拍摄

图5 45°偏角拍摄

图6 60°偏角拍摄
2.2.2 校正步骤
校正步骤可以分为3个主要步骤,分别是横向缩放、纵向缩放和比例因子调整。校正的前置环节是确定图像中焦平面与被摄物体平面的交线,在自动对焦拍摄条件下,原始图像竖直方向中点的水平线即为该交线,通过该交线确定标尺刻度,便可在之后的裁切图片中确定该交线。
横向缩放依据第2部分所述的二阶泰勒展开进行处理,在图像垂直于交线的方向测量到交线的偏移距离以及在该水平位置处标尺的增量计算公式(8)中的未知参数C、D,由于标尺的标准宽度为2 cm,得到距离交线距离为x的水平线的缩放比例系数k如公式(13)所示。
(13)
依据双线性插值的方法对调整后的水平线进行插值,横向缩放后的结果如下图7、图8、图9所示。

图7 30°偏角横向缩放

图8 45°偏角横向缩放
纵向缩放环节与横向缩放环节类似,重复部分不再赘述,纵向缩放与横向缩放的处理步骤区别主要在于缩放系数是一个与到交线距离有关的函数,在进行纵向缩放时理论上任意一点的缩放系数均不相同,在计算纵向缩放时将图像沿着纵向进行分割,保持在分割的一段小区间内缩放比例系数一致。不同偏角情况下经计算得到纵向缩放后的结果,如图10、图11、图12所示。

图9 60°偏角横向缩放

图10 30°偏角纵向缩放

图11 45°偏角纵向缩放

图12 60°偏角纵向缩放
在完成横向缩放和纵向缩放后,图像上不同区域沿着纵向和横向的单位长度是一致的,消除了偏离焦平面产生的近大远小现象。此时还存在投影偏差需要校正,通过比例因子将两个正交方向的单位长度调整一致即可完成对图像的校正,校正结果如下图13、图14、图15所示。

图13 30°偏角比例因子调整

图14 45°偏角比例因子调整
2.2.3 比对校正
使用通用图像处理软件PHOTOSHOP中的透视、切边、拉伸功能对分别对30°、45°、60°偏角拍摄图片进行校正如图16~18所示。

图15 60°偏角比例因子调整

图16 30°偏角ps校正

图17 45°偏角ps校正

图18 60°偏角ps校正
3 实验结果和讨论
3.1 实验结果
经过泰勒二阶展开校正后的足迹图像与垂直拍摄的图像进行重合,足迹大小吻合,花纹类型反映一致,种属条件一致。将足迹照片制作成原大,测量鞋长、鞋宽,选取a、b、c、d、e5个特征点进行测距(标注于图13、图14、图15),所得结果如表1所示。采用相同的方法对ps比对结果进行测距(标注于图16、图17、图18),所得结果如表2所示。

表1 泰勒展开法特征点测距表
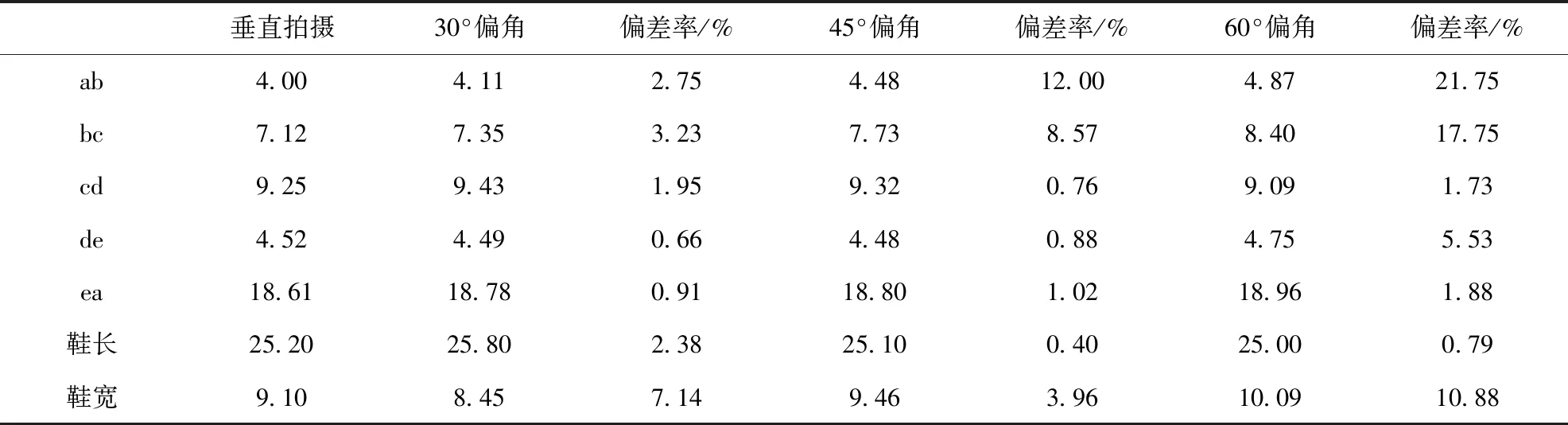
表2 ps法特征点测距表
3.2 实验讨论
经过对垂直拍摄结果和偏角拍摄校正结果进行比较,发现两者所反映的种类特征一致,细节特征吻合度高,在偏角小于45°时偏差一般不超过3%,具备同一认定的条件。与使用通用软件ps校正结果比较,本文所提的方法在校正效果上有明显的优势,当偏角达到45°时,ps校正图像的偏差率可能达到10%,无法应用于法庭科学的检验。结合实验对偏角摄影图像校正还有两个细节需要展开讨论。
一是偏角的极限。在偏角摄影的过程中由于偏角导致原有图像在竖直方向上被显著压缩,该信息丢失是一种不可逆过程,使用泰勒二阶展开和插值方法只是根据残留信息对原始信息的一种估计和推测。理论上图像边缘对比度和清晰程度必然下降,当偏角达到60°时,部分特征点的边缘出现了比较明显的模糊现象,从实验结果看60°可以认为是偏角拍摄的极限。需要指出偏角拍摄极限还受制于花纹曲线,某些复杂的花纹可能在更小的偏角时已无法复原,因在观察时逐步增大偏角,在确保特征都能得到反映的情况下找到最佳的偏角拍摄角度。
二是精度和复杂性的关系。本次实验采用的是基于透视关系的Taylor二阶展开的方法,算法中采用了多次近似,如使用Taylor二阶展开近似地表示偏离焦平面导致的长度上的变化,近似地利用图像上一点到交线的距离表征偏离焦平面的程度。本文采用了最简单的形式校正了偏角拍摄造成的非线性畸变。近似算法已经能够在一定的偏角范围内校正图像并达到同一认定的要求,满足了公安工作的需要,改进和优化模型提高的精度,但会显著的增加计算量和算法复杂度。
4 结论
基于Taylor二阶展开的双线性插值偏角足迹校正技术可以在60°偏角拍摄的范围内校正变形图像,所得到的图像与垂直拍摄的图像相比种类特征反映一致,个体细节特征反映良好偏差程度小,可用于足迹的同一认定。该技术效果好,操作简便,计算量小,使得拍摄角度可以不再不局限于垂直于痕迹面,有力地丰富了传统的物证摄影技术。
