基于量子算法的量子态层析新方案*
2019-10-23杨乐李凯戴宏毅张明
杨乐 李凯 戴宏毅 张明†
1)(国防科技大学,智能科学学院,长沙 410073)
2)(国防科技大学,文理学院物理系,长沙 410073)
3)(国防科技大学,量子信息交叉中心,长沙 410073)
在经典信息可有效制备为量子态和量子算法可物理实现的条件下,深入研究了量子算法如何有效改善基于线性回归估计的量子态层析算法的时间复杂度问题.在已有的量子算法基础上,形成了量子态层析的新方案.与现有的经典算法相比,本文所提方案需要引入量子态制备和额外的测量环节,但能显著降低量子态层析的时间复杂度.对于维数为d的待重构密度矩阵,当所用的量子算法涉及的矩阵的条件数κ和估计精度ε的倒数的复杂度均为O(polylogd),且所需同时制备的量子态数目规模是O(d)时,本方案可将量子态层析整体算法的时间复杂度从O(d4)降为O(dpolylogd).
1 引 言
量子态层析(quantum state tomography),也称为量子态估计(quantum state estimation)[1],是通过测量数据来推断被测量子态的方法.对于n量子比特构成的量子系统,其维数 d=2n,因而量子态层析任务的时间复杂度随着问题规模的增加成指数增长.量子态层析分为2个阶段,即测量阶段和使用测量数据重构量子态阶段.当面对的量子系统维数较高时,这2个环节的时间复杂度会很大.例如文献[2]的研究者面对8离子的量子系统,耗费10多个小时在测量和数据采集的环节,而又花费了将近一周时间使用数据进行量子态重构.因此,选择合适的测量集及重构方法是解决量子态层析问题的关键.量子态重构有多种方法,如线性估计[3]、线性回归估计[4,5]、极大似然估计[6,7]、贝叶斯均值估计[8,9]等,这些方法各有优势和不足.
量子算法是应用在量子计算机上的算法.对于经典算法的难解问题,有些可以找到量子算法使其在有效时间内解决[10,11]; 有些在一定条件下可以加速问题的求解,从而显现出量子算法的优势[12,13].从机器学习的角度,可以将量子算法整体看作是一个黑盒,把测量数据及态生成源的数据作为训练集合,训练得到量子态重构的模型.这属于使用量子算法解决量子问题的范畴[14].一个自然的问题是:对于量子态层析的重构过程,使用量子算法能否使其得到加速,从而使时间复杂度下降? 目前使用量子算法实现量子态重构的相关研究还不多,并且还未发现从时间复杂度角度来分析量子态重构的量子算法与经典算法相比是否有优势的研究内容.
量子态重构过程的经典算法有多种,不同算法又分为多个环节,不同环节中的步骤涉及不同的操作,这些操作对应的量子算法也有不同的实现方法,因而并没有一个统一的量子算法来实现重构过程.本文关注的问题是: 对于使用线性回归模型估计未知状态参数的量子态重构过程,使用量子算法进行处理是否值得,在什么条件下使用量子算法会加速任务的完成.选择使用线性回归算法的估计过程,原因在于它是几种重构算法中重构速度快于极大似然估计和贝叶斯估计的一种,并且通过求解受约束的优化问题[15],避免了线性估计算法的重构矩阵可能存在负本征值的问题.通过在重构算法的不同步骤中选择相应的量子算法,可以形成一个实现量子状态重构的整体量子算法,然后从时间复杂度的角度将其与经典算法进行对比分析.
当要求的精度和重构过程涉及到的矩阵条件数等指标,满足使用量子算法进行加速的条件,且所需制备的量子态数目与系统维数成正比时,整个量子算法实现过程可以将目前使用线性回归估计实现量子态重构过程的总体时间复杂度,由O(d4)降低为 O (dpolylog(d)).
本文后续内容安排如下: 第2部分叙述基于线性回归估计的经典重构算法,第3部分展示使用量子算法处理量子态重构的基本流程,第4部分对比分析研究了分别使用经典算法和量子算法的时间复杂度,第5部分是算例,第6部分是结论.
2 基于线性回归估计的经典重构算法
在测量存在高斯噪声时,可以使用基于线性回归估计的重构算法,来高效地重构量子状态[4].要通过测量数据得到系统密度矩阵 ρ 的重构矩阵,可以使用如图1所示的2个环节来进行.
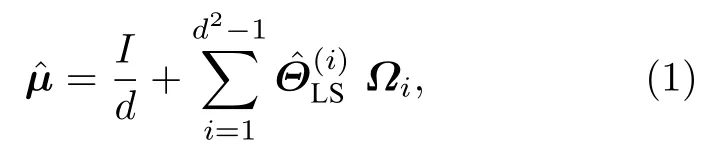
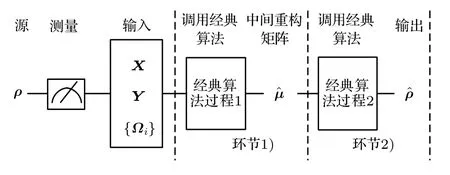
图1 基于线性回归估计的经典重构算法Fig.1.Classical algorithm of quantum state tomography via linear regression.
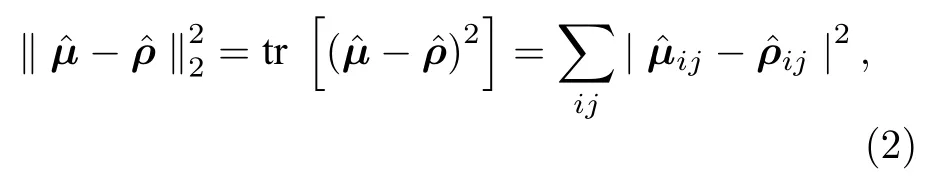
下面分别叙述如何得到方程(1)和方程(2),以及它们的求解过程.
2.1 使用测量数据重构伪线性估计矩阵(环节1)
可以使用线性回归估计[4],通过5个步骤得到量子状态中的未知参数,并使用估计出的参数重构出.下面对这5个步骤进行简要叙述.
1)设量子系统的维数是d.选取刘维尔空间(Liouville space)中的一组完备正交基,记为
2)分别将待重构的量子状态和测量基在刘维尔空间中展开,得到相应的由展开系数构成的向量.
3)计算测量算子作用于量子态所得到的测量结果的概率,可以使用2)中的量子态和测量基在刘维尔空间中的展开系数表示测量结果概率.
4)结合测量结果概率和实际测量的频率,得到描述量子状态的未知参数 Θ 的线性估计模型:

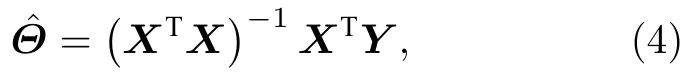
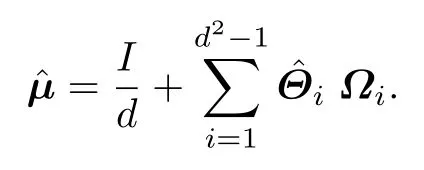
2.2 求与矩阵最接近的目标矩阵(环节2)
这个问题可以表述为[15]: 给定一个迹为1的厄米矩阵,在2-范数下可以找到与其最接近的密度矩阵(迹为1且只含有非负本征值的厄米矩阵)
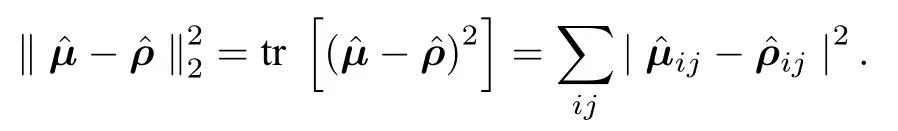
要求解这个最小二乘的估计问题,计算量比较大[15].但文献[15]根据表达式的物理意义,给出了如下的优化解决方法.
2)令i=d ,累加器 a=0 .
3 量子态重构的量子算法处理过程
整个使用量子算法处理量子态重构的过程如图2所示,可以分为以下几个环节:
准备环节 根据测量数据及选定刘维尔空间中的基,制备相应的量子态
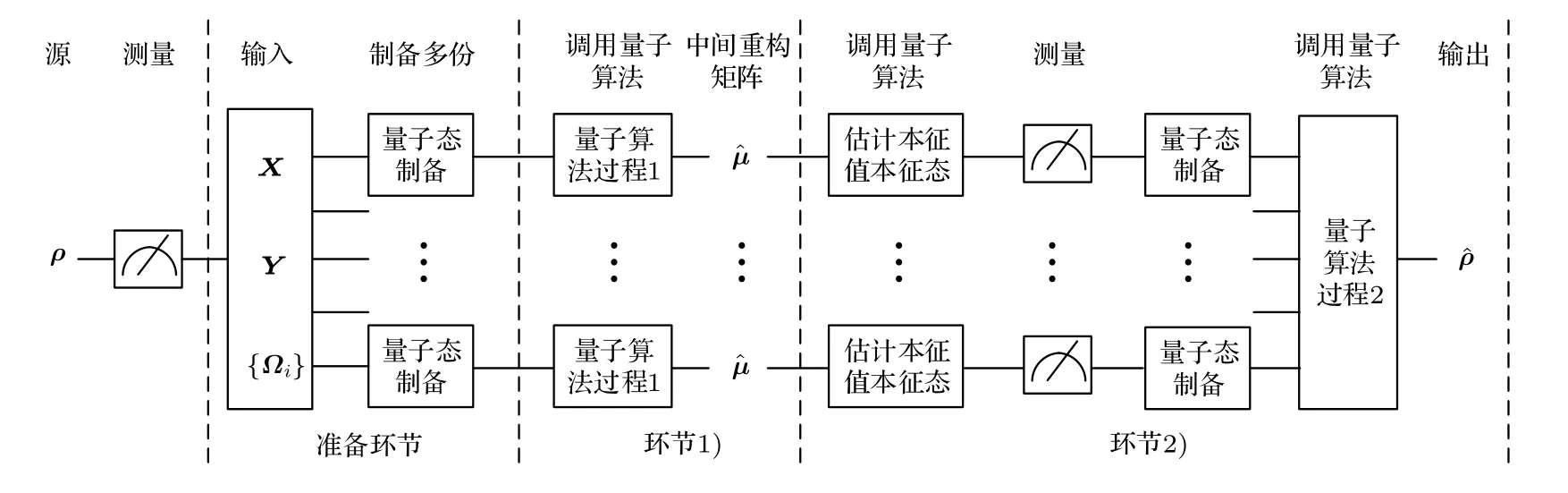
图2 整体量子算法简明过程Fig.2.Concise process of the whole quantum algorithm.
对于量子态层析,对量子态产生源进行测量,得到的数据是经典数据,因而需要在环节1)之前引入准备环节,来制备量子数据这里对于矩阵的量子数据的符号仍使用原符号,例如矩阵X和 Ωi即表示它们各自的量子数据; 对于向量的量子数据,使用右矢形式,例如 | Y〉 表示向量Y的量子数据.暂不考虑量子态制备的量子算法实现过程,而假设能够有效制备量子态.图2中环节1)和环节2)并行处理多个量子态,其中每个单独过程与量子态重构的经典算法基本一致,但注意到在经过本征值和本征态的估计算法之后,需要引入测量以及量子态制备环节,以与后面调用量子算法过程相衔接.
图2涉及的量子算法,可归纳为以下几种:1)矩阵乘法的量子算法[16]; 2)矩阵求逆使用到的求解线性方程的量子算法[17]; 3)求解矩阵本征值和本征态的相位估计算法[17]; 4)对本征值进行排序的排序算法[18,19].使用量子算法的具体过程如图3和图4所示,下面简要叙述相应的量子算法.
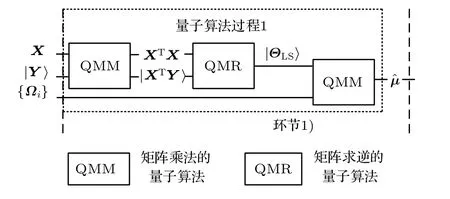
图3 量子算法过程1: 基于线性回归模型重构算法的量子算法Fig.3.Quantum algorithm process 1: quantum algorithm based on quantum state tomography via linear regression.
3.1 矩阵乘法的量子算法[16]
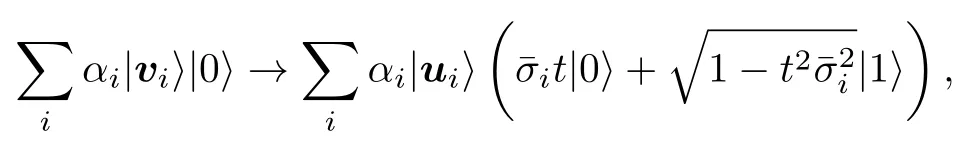
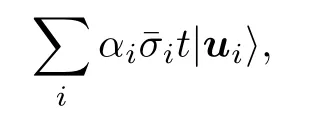
其中 σi的估计值满足设输入态则输出态即为 A |b〉 .包含测量后选择操作在内的整个矩阵乘法的量子算法的时间复杂度是κ 是矩阵A的条件数,ε是精度.在计算矩阵间的乘法 A ×B 时,可以将B按列展开为 { bi} ,然后使用量子算法并行处理A|bi〉.
3.2 矩阵求逆的量子算法[17]
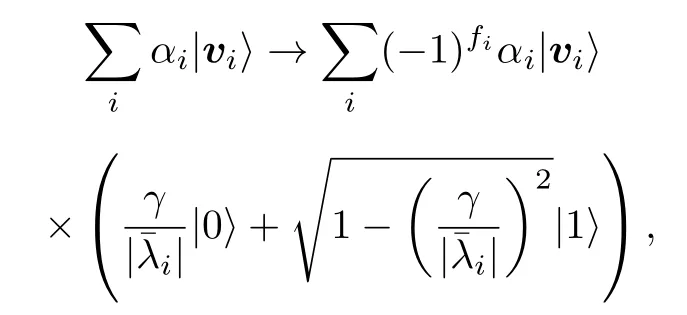
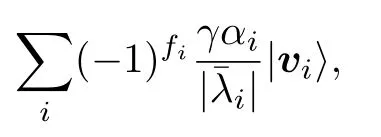
3.3 求解矩阵本征值和本征态的相位估计算法[17]
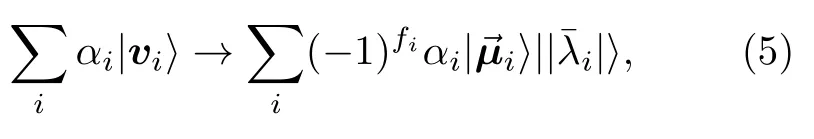
此算法是基于矩阵求逆量子算法的部分过程实现的,相比于矩阵求逆量子算法,由于没有引入辅助量子比特并进行测量,所以该量子算法的时间复杂度为
3.4 量子排序算法
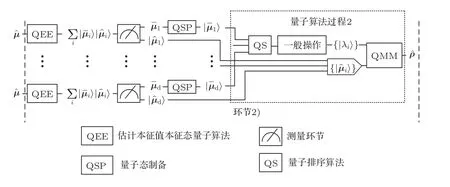
图4 量子算法过程2Fig.4.Quantum algorithm process 2.
以量子比较逻辑门(comparison gate)为基本单元,可以构造排序算法的黑盒[18].将量子态形式的矩阵的所有本征值的估计值作为黑盒的输入得到的输出结果是按本征值大小排列的量子态.文献[19]则指出,通过使用受控的比较逻辑门可以实现归并排序过程,同样可以实现量子态本征值的排序.在排序之后,使用与第2.2节中的第1)到5)相对应的量子操作,即可得到目标密度矩阵.
4 经典和量子求解思路的时间复杂度对比
量子算法与经典算法过程的不同环节的时间复杂度如表1所示.
下面分别具体分析量子态层析任务各个过程的经典算法和量子算法的时间复杂度.
4.1 经典算法各环节的时间复杂度
在第2节描述的使用经典算法进行量子态重构的2个环节,第1)个环节使用最小二乘法求解模型,在信息完备的测量集合下,X是d2×(d2-1)矩阵,Y是d2×1列向量,因此XTX以及XTY的计算复杂度均是O(d4);(XTX)-1的时间复杂度一般是O(d6),但在选择的测量集合满足一定条件下,(XTX)-1的时间复杂度可以降为O(d4).第1)环节最后1步中,通过估计出的参数,使用方程(1)重构伪线性估计矩阵的时间复杂度是O(d4),原因是集合{Ωi}有d2个元素,而每个元素Ωi是d×d矩阵,中的(d2-1)个数与{Ωi}(i/=0)相乘.但正如文献[15]指出的,若使用Pauli算子的张量积作为量子系统刘维尔空间中的一组基,由于每一个d×d的基矩阵都只有d个非0元,则使用方程(1)的重构过程的时间复杂度可以降低为O(d3).第2)个环节计算方程(2),使用文献[15]的算法,在寻找与矩阵最接近的过程中,需要求解矩阵的本征值和本征态,该步骤的时间复杂度通常是O(d3).对得到的的本征值进行排序,常用的经典排序算法时间复杂度是O(d).在排序之后,使用基本的加法和除法操作,得到矩阵的本征值{λi},该过程时间复杂度是O(d).最后,通过{λi}和的本征态重构出目标矩阵,此过程的时间复杂度是O(d3).
总结整个过程,经典算法的最大时间复杂度出现在对矩阵(XTX)-1求逆的步骤当中,一般为O(d6).选择合适的测量集时,可以使该步骤复杂度降低为O(d4).
下面分析量子算法实现过程的时间复杂度.
4.2 量子算法各个环节时间复杂度分析
4.2.1 量子态制备的时间复杂度
在使用量子算法处理量子态重构过程的3个环节中,有2个环节涉及使用测量得到的经典数据制备量子态: i)准备阶段; ii)在环节2)中,测量得到本征值后,为在后续使用量子算法进行排序,须制备量子态以存储本征值.不同制备量子态的量子算法时间复杂度不同.文献[16]给出了几种不同量子算法的时间复杂度:其 中是向量 x 的最大值与最小值的比率,d是向量维数,ε是要求的精度,c是某个常数; 2)O (log(d)/ε2);可以观察到,1)是对数的多项式时间复杂度; 1),2)和4)是d的对数的时间复杂度; 3)是精度 1 /ε 的对数时间复杂度.但还没有发现使,d,1/ε 同时实现对数时间复杂度的量子算法.当1/ε=O(polylogd)时,1),2),4)均可以实现 O (polylogd)的时间复杂度.但由于1)与4)均与 κ 有关,因此在表1中,选取了 O (log(d)/ε2)作为量子态制备的时间复杂度的代表.
在图2所示的准备环节,可以使用测量得到的经典数据制备N个量子态,后续可以使用量子算法过程1以及估计本征值和本征态的量子算法,对这些量子态并行处理.但是制备多份量子态会导致在准备环节以及环节2)中的量子态制备过程的时间复杂度增大.制备N个量子态相应的时间复杂度是 O (Nlog(d)/ε2).若制备的量子态个数N的规模是 O (d),则相应的时间复杂度为 O (dlog(d)/ε2).这里假定N的规模是 O (d),是考虑到对d维量子系统来说,其本征值个数不超过d,在不同本征值之间大小相差不是特别悬殊时[11],测量得到这些本征值所需制备的量子态个数是 O (d).当 1 /ε 是log(d)的多项式规模时,量子态制备过程的最大时间复杂度是 O (dpolylogd).
4.2.2 矩阵乘法量子算法的时间复杂度
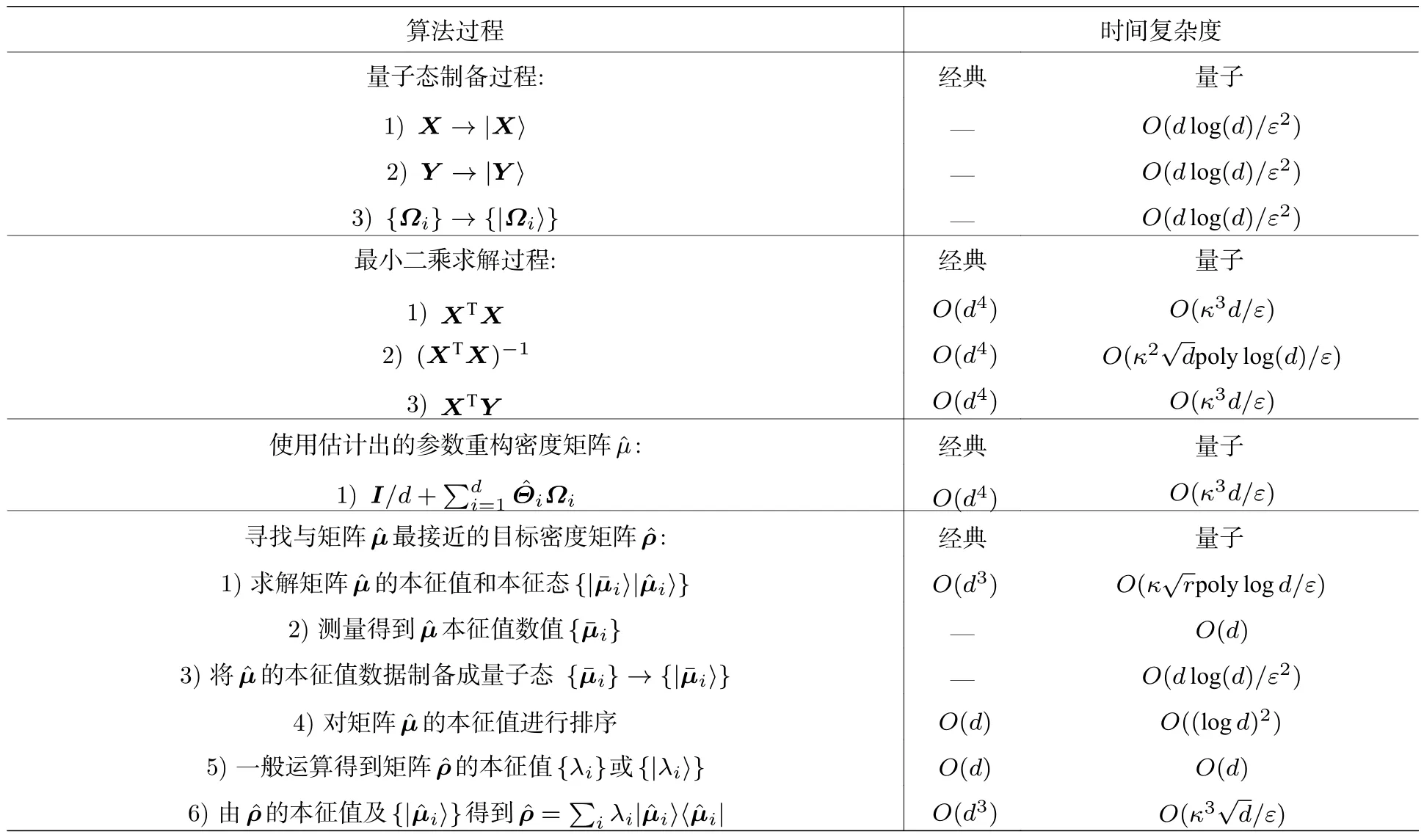
表1 量子态重构过程不同环节的量子算法与经典算法时间复杂度的对比Table 1.Time complexity comparison of each step between quantum algorithm and classical algorithm for reconstructing quantum state.
4.2.3 矩阵求逆量子算法的时间复杂度
使用基于奇异值估计量子算法的矩阵求逆算法,文献[17]分析了其时间复杂度,为O(κ2polylog(d)‖A‖F/ε).对于求解量子线性系统的算法[12],可以假设在量子态层析任务中,如果选择正四面体测量基和正六面体测量基,可以得到矩阵A是对角矩阵[4],同样有成立.因此在量子态重构过程中,使用基于奇异值估计量子算法解矩阵求逆过程的时间复杂度是当κ和1/ε都是log(d)的多项式规模时,使用矩阵求逆量子算法的最大时间复杂度是
下面解释为何要在估计本征值之后引入测量环节以及量子态制备环节.通过量子算法得到矩阵的本征值量子态、本征态,不同的本征值量子态、本征态之间是纠缠的,而后续的量子排序算法要求输入全部的本征值量子态.因而需要引入测量环节得到本征值,再将其转化为量子态数据.例如,通过表2的量子算法后,若得到的态是是存储了本征值估计值的量子态,是相应的本征态.对处于寄存器中的本征值估计值进行测量,当测量结果是时,态 | Ψ〉 塌缩到上; 测量结果是时,| Ψ 〉 塌缩到上.因此,在求解矩阵的本征值和本征态的量子算法之后,通过引入测量环节提取出本征值信息并且分别进行存储; 为与后续的排序量子算法衔接,还要将测量得到的本征值信息制备成量子态,从而贯通整个使用量子算法处理量子态层析的过程.
4.2.5 本征值排序量子算法的时间复杂度
4.2.6 量子态重构过程整体量子算法的时间复杂度
总结上述分析过程,当不考虑实现的资源代价,而只追求降低整个过程的时间复杂度时,若相关矩阵的条件数 κ 及要求的精度 1 /ε 都是log(d)的多项式规模时,准备环节及环节2)中的量子态制备过程是整体量子算法中时间复杂度最大的过程,相应的时间复杂度是 O (Npolylogd).当制备的量子态的个数N的复杂度是 O (d)时,整个量子算法过程的时间复杂度是 O (dpolylogd).矩阵乘法的量子算法的时间复杂度也是 O (dpolylogd).
5 算 例
本节用一个算例来说明整体量子算法的可行性.考虑单qubit的量子态层析,记生成源为 ρ ,此时系统的维数 d=2 .选取刘维尔空间中的一组基{Ωl}:
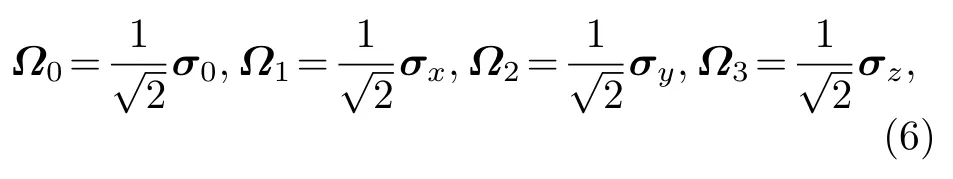
其中,l=0,1,2,3;σ0=I2×2,σx,σy,σz分别为Pauli算子.选择信息完备的正四面体测量基对ρ进行测量,得到测量基在刘维尔空间展开系数构成的可逆矩阵X以及不同测量结果的频率构成的向量Y:
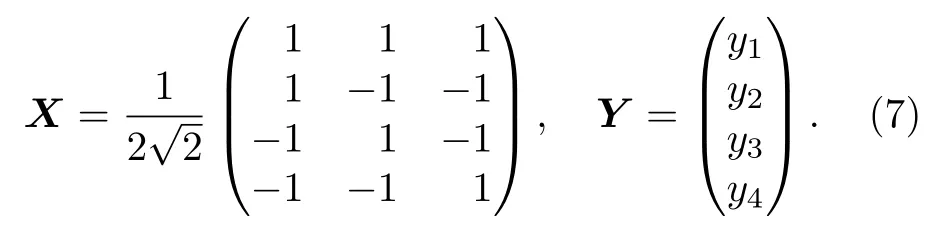
以下对照图2—图4叙述量子算法过程.
5.1 准备环节
5.2 调用量子算法过程1求解中间重构矩阵
量子算法过程1如图3所示.首先调用矩阵乘法量子算法由 X ,XT,|Y〉 计 算出 | XTY〉, XTX.
使用矩阵乘法量子算法[16]计算矩阵与向量的乘积,输入态由矩阵右奇异向量表示,输出态由矩阵左奇异向量表示,即可以得到以下输入态到输出态的变换过程:
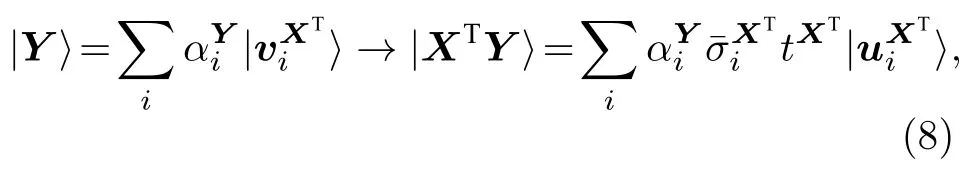
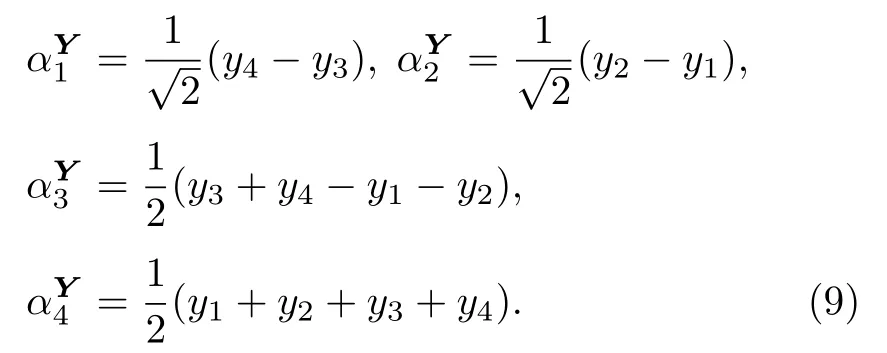
由于 XT的奇异值均为同一量子算法过程的估计精度相同,因而矩阵 XT奇异值的估计值相等.为简明表达计算过程,假定估计值与待估计值相等,即最终得到
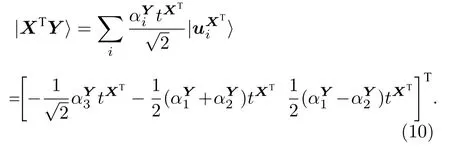
对于 XTX ,设 X=[X1X2X3],可使用矩阵乘法量子算法同时求解|XTX1〉,|XTX2〉,|XTX3〉,得到
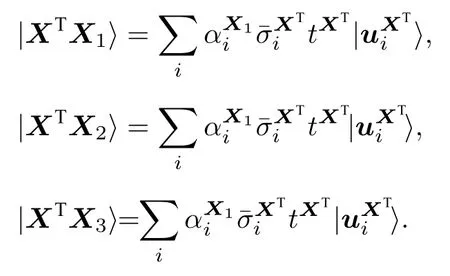
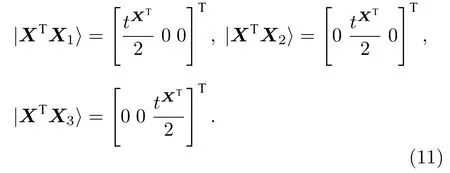
2)使用矩阵求逆量子算法计算得到|Θ〉
设A=XTX,|b〉=|XTY〉,A|Θ〉=|b〉,要得到|Θ〉=|A-1b〉.基于奇异值估计的量子算法的存储结构要求存储的是矩阵列向量元素,以及矩阵行向量的2-范数[20].由矩阵乘法量子算法计算得到的|XTX1〉,|XTX2〉,|XTX3〉对应矩阵A的列向量.由于选取的测量基使得A是对角矩阵,由对角矩阵对称性可知|XTXi〉中的元素相当于矩阵A的行向量中的元素,因而满足使用奇异值估计量子算法的存储结构,可以使用|XTXi〉 直接参与后续量子算法运算过程,而不必经过转置操作.因而
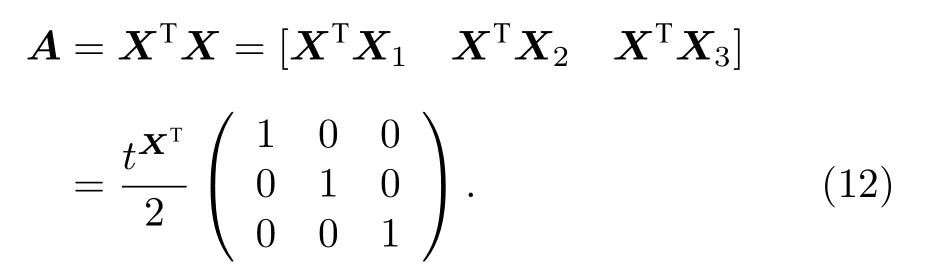
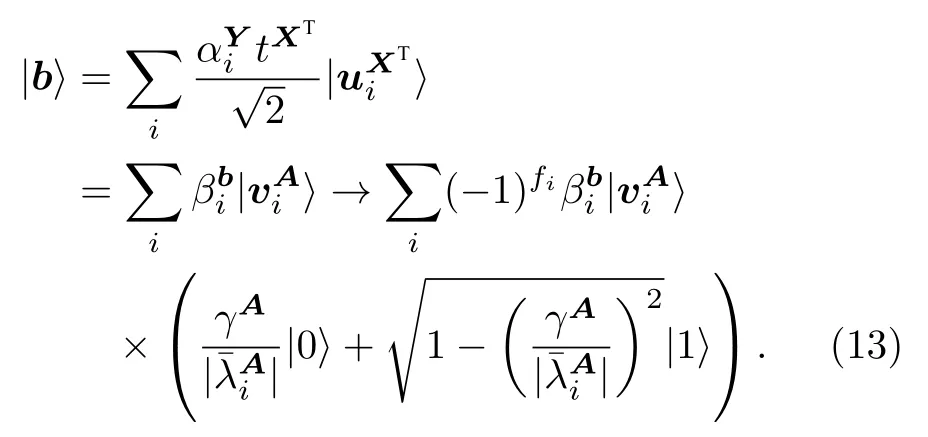
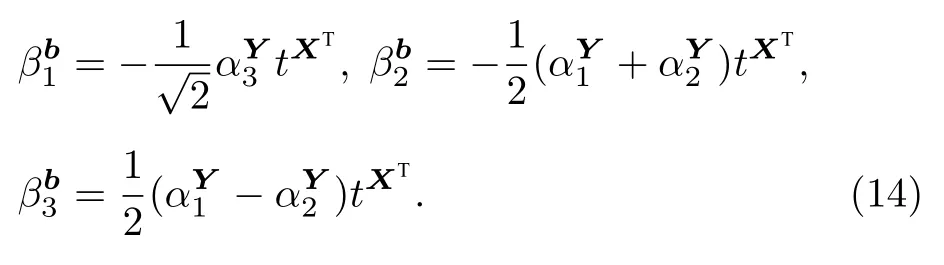
对方程(13)输出量子态的辅助量子比特位进行测量,若结果为 |0〉 ,则输出态塌缩到所需的矩阵求逆结果:
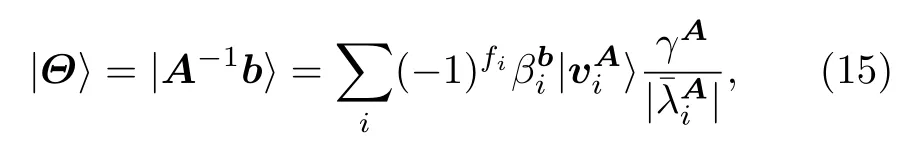
其中,γA=O(1/κ),κ 是矩阵A的条件数.A是正定厄米矩阵,对A进行奇异值分解,可以得到A的奇异值进而得到相应的本征值tXT/2,因而
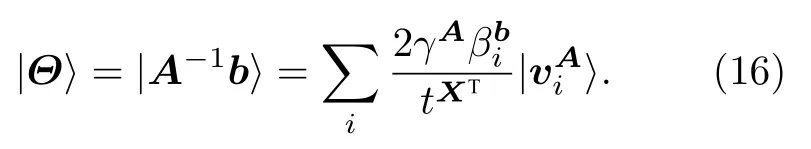
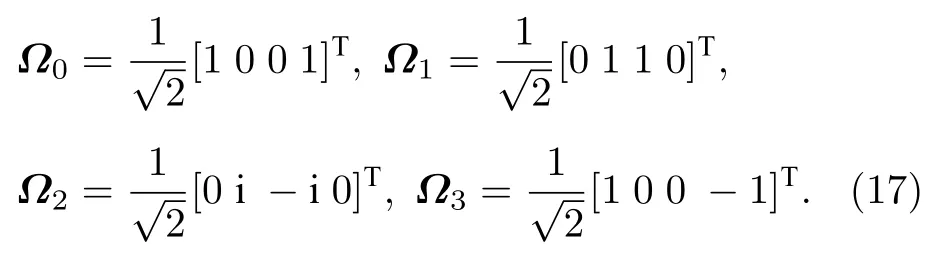
记
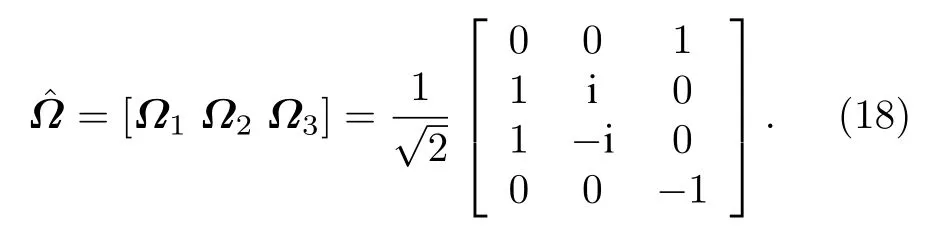
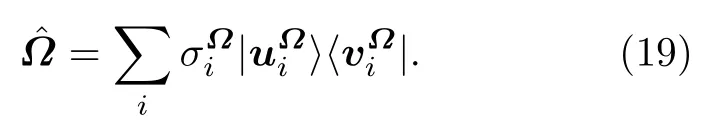
以方程(16)得到的结果为输入态,调用矩阵乘法量子算法,可以得到如下变换:
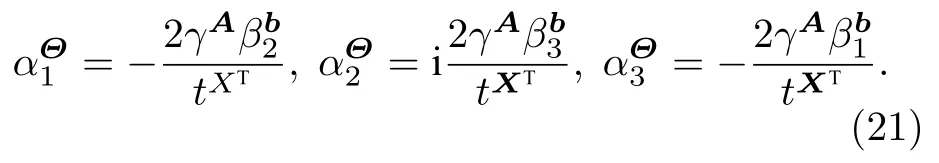
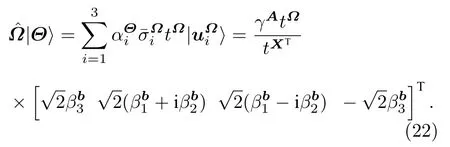
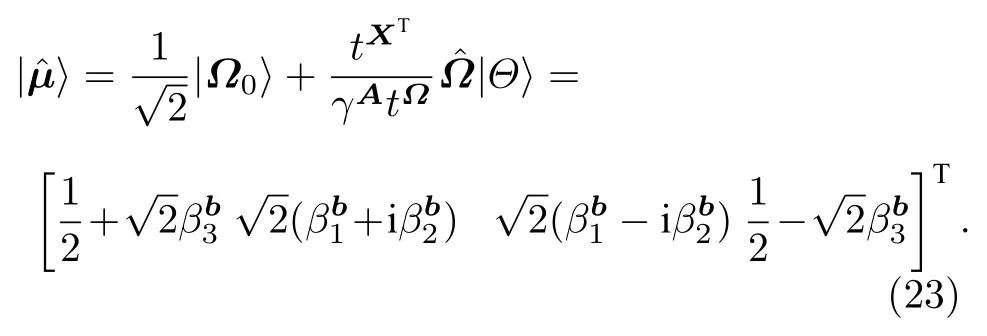
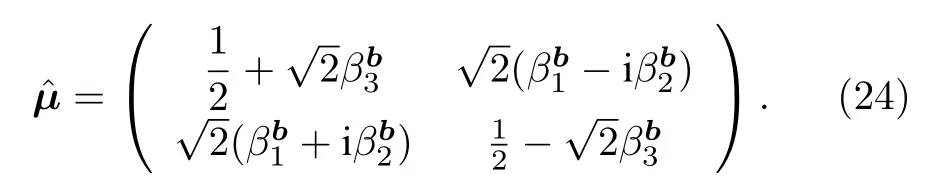
5.3 计算目标重构矩阵
设方程(24)中
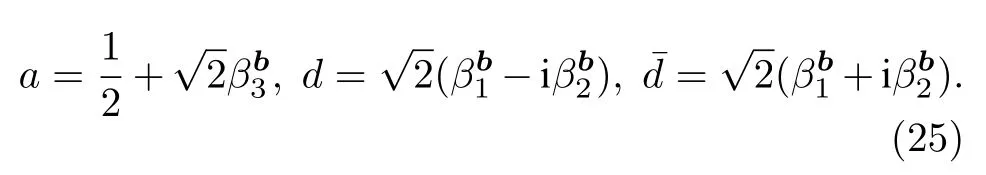
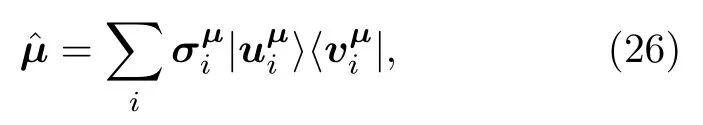
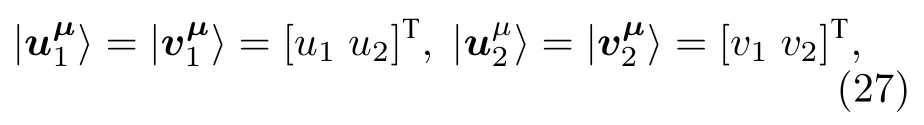
可以计算得到
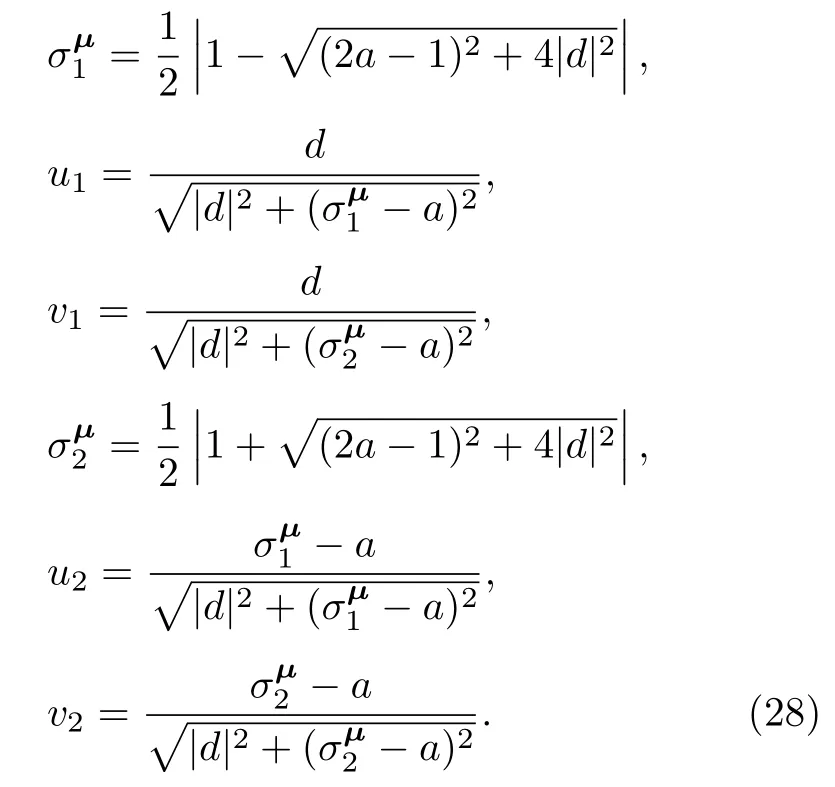
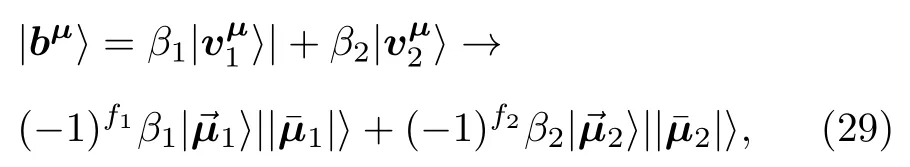
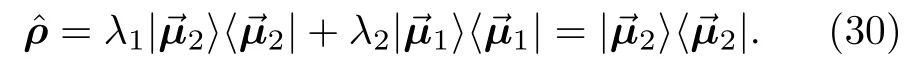
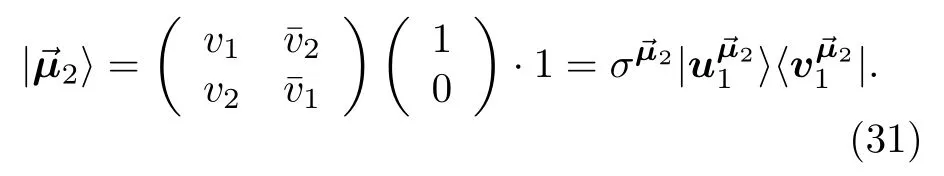
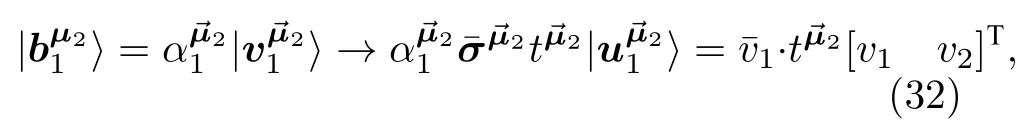
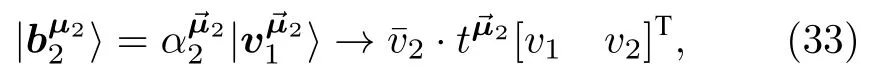
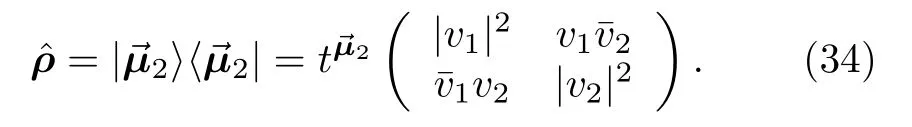
将方程(9),(14),(25)及(28)的表示代入到方程(34),并去掉因子即得到最终的使用输入数据Y=[y1y2y3y4]T表示的重构矩阵:
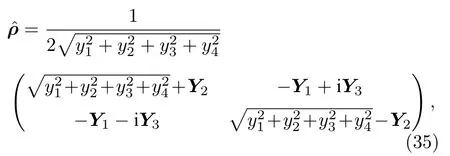
其中
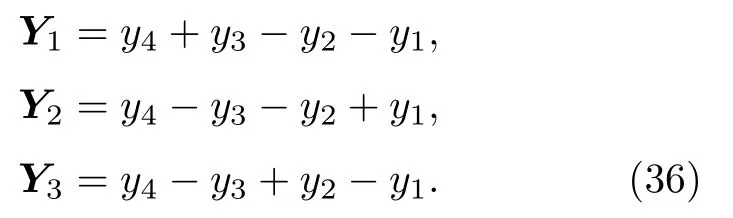
6 结 论
本文深入探讨了处理量子态重构的整体量子算法.通过在重构过程的不同步骤使用相应的量子算法,得到了实现量子态重构的整体量子算法新方案.对比分析表明: 对于d维密度矩阵,经典算法的最大时间复杂度出现在矩阵乘法过程中,为O(d4); 而对于量子算法,在精度 ε 和矩阵的条件数κ等指标满足使用量子算法进行加速的条件下,即1/ε, κ 的复杂度均为 O (polylogd)时,量子算法的最大时间复杂度出现在量子态制备过程中,为O(Npolylogd),其中N为制备量子态的数目.当制备的量子态数N的规模是 O (d),即可得到中间重构矩阵所有的本征值时,量子算法的时间复杂度为 O (dpolylogd).
通俗地说,本文主要试图回答如下问题: 如果量子计算机可物理实现且量子算法可以在量子计算机上物理实现,那么量子算法在多大程度上可以降低量子态层析的时间复杂度? 研究表明,如果量子态可以高效制备,那么采用量子算法可将量子态层析整体算法的时间复杂度从 O (d4)降为O(dpolylogd); 如果量子态无法高效制备,量子态层析整体算法的时间复杂度从 O (d4)降 为 O (d3).因为对于量子态制备问题,制备维数为d2、规模为O(d)的量子态,时间复杂度是 O(d3).因此本研究从一个侧面证明了量子态能否高效制备已成为量子算法降低时间复杂度的瓶颈。
最后简要探讨本文所提方案的物理实现可行性.文献[20]的作者讨论了奇异值估计量子算法能够实现的前提是构造出一种合适的存储经典数据的数据结构,并在文章最后给出了具体的构造形式,因而是能够物理实现的.由于方案涉及的矩阵乘法、矩阵求逆以及本征值和本征态估计的量子算法均是基于奇异值估计的量子算法,因而理论上是可以物理实现的.方案涉及到的其他过程,即量子态制备、测量以及量子排序,是理论上能够实现或已经实现的[14,19,21].因此总体来说,本文所提方案具有物理实现的可行性.
若A为正定厄米方阵,矩阵的奇异值分解也就是矩阵的本征分解,矩阵A的奇异向量 | vi〉 与 其本征向量 | μi〉 相等.若A为非正定厄米方阵,将矩阵A分别用本征分解和奇异值分解来表示,有
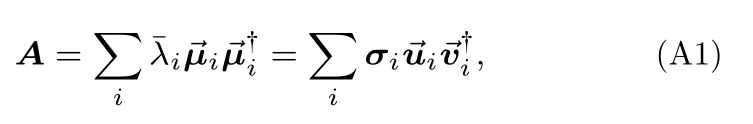

表A1 求解厄米矩阵本征值和本征态的量子算法[17]Table A1.Quantum algorithm for calculating the eigenvalues and eigenstates of Hermite matrix[17].
