法兰螺栓松动的超声导波监测方法

杜 飞， 张子涵， 徐 超

(西北工业大学 航天学院, 陕西 西安 710072)

0 引言

在实际工程中,管道应用广泛，法兰螺栓连接是管道连接的主要方式。随着工程中对管道等可靠性要求的日益提高，法兰螺栓连接对可靠性的要求也越来越高。螺栓的松动会直接导致密封失效，而管道连接处的泄漏事故占比较高[1]。因此，如何对法兰螺栓松动进行准确监测已备受关注。

吴斌等[1]提出利用机电阻抗技术监测法兰螺栓的松动，但在利用压电片监测机电阻抗变化时，其仅对压电片附近局部范围较敏感。超声导波因灵敏度高，监测范围广,已被广泛用于结构健康监测[2-3]中。Yang等[4]首次提出利用超声导波监测螺栓预紧力，随后学者对此开展了广泛研究。Wang等[5]提出利用超声导波幅值作为拧紧指标，对单个螺栓的预紧力进行监测。吴冠男等[6]提出利用混沌导波的Lyapunov维数等作为拧紧指标进行监测。由于频散、多模态等因素，超声导波信号较复杂，因此，Wang等[7]、DU F等[8]提出了基于时间反转导波的螺栓预紧力监测方法，并以时反后导波信号的幅值为拧紧指标进行预紧力监测。

上述超声导波方法均是针对平板间的螺栓连接，且均用于单个螺栓松动的情况。然而，法兰螺栓连接的是2个圆管结构，圆管中导波具有纵向、弯曲、扭转3种模态[9]，导致导波信号复杂，同时法兰上螺栓数目多，螺栓松动监测难。因此，本文提出利用导波信号的均方根偏差进行螺栓松动监测，同时根据均方根偏差值的分布对松动螺栓位置进行初步判断，利用有限元法和实验对上述方法进行了验证。

1 法兰螺栓导波监测原理

1.1 管道中的超声导波

弹性波在无限长空心圆管中传播时，各质点的位移分量[10]为

(1)

式中：ur，uθ，uz分别为径向、周向、轴向位移分量；ω为角频率；ξ为波数；Ur，Uθ，Uz为径向、周向、轴向3个方向上用Bessel函数表示的位移幅度；n=0,1,2,3，…为周向阶数。

超声波在管道传播时有纵向、扭转和弯曲模态3种传播模态。以内径81 mm、外径86 mm的铝管为例，当其弹性模量为6.9×104MPa，泊松比为0.35，密度为2 700 kg/m3时，弯曲模态的群速度计算结果如图1所示。图中，F(n，m)中n为弯曲模态的阶数，m为模数。

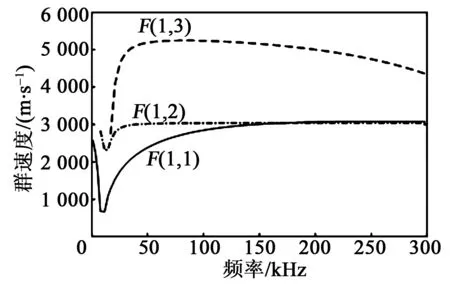
图1 铝管中弯曲模态群速度的频散曲线

1.2 超声导波监测螺栓松动原理

工程实际中，材料表面不完全光滑，接触界面上存在高低不平的微凸体，接触区域的真实接触面积取决于接触微凸体的数目及大小。弹性波在通过接触界面时，透射信号的能量取决于接触界面真实接触面积[4]。另一方面，根据接触力学的理论，接触界面的真实接触面积随着接触压力发生变化。界面接触压力由螺栓连接的扭矩大小和接触表面粗糙度决定。弹性范围内，接触界面间接触压力与螺栓上施加的扭矩关系为

(2)

式中：p为压力；T为螺栓扭矩；K为扭矩系数，一般取K=0.2;d为螺栓的公称直径。因此，通过对此标准扭矩下透射超声导波与松动后透射超声导波，可以检测螺栓预紧力的变化情况。

1.3 螺栓拧紧指标

螺栓连接状态发生改变后，透射过螺栓连接部的导波信号会产生相应的变化。现有方法通常采用导波幅值或能量相对标准扭矩下的变化量作为拧紧指标[4-5,7-8]进行松动监测。然而，由于管道中导波模态较多，为激励出单一模态导波需要压电片阵列对管道同时进行激励，对硬件的要求较高。若采用单个压电片激励，则产生的导波模态复杂，导波信号透射过法兰后更复杂。为利用导波信号的幅值或能量进行检测，需要仔细挑选接收信号中较敏感部分，应用不便。另一方面，导波信号在不同拧紧状态下进行对比时，两者变化程度用均方根偏差表示，即

(3)

式中：Vi为螺栓松动工况下的信号幅值；V0i为标准工况下的信号幅值；N为所取时域范围内数据点的个数。

本文采用均方根偏差作为拧紧指标，同时采用压电片依次进行激励的方式进行监测，此时距离压电片较近的螺栓对信号影响较大。通过对比不同接收压电片信号的均方根偏差，则能反映松动螺栓的位置。

2 法兰螺栓松动导波监测的数值模拟

为验证上述超声导波监测方法的可行性，建立了考虑压电效应的三维有限元模型，用理论研究不同螺栓预紧力及螺栓松动位置对导波信号的影响。为了简化模型，降低计算耗费，有限元模型中忽略螺栓及螺栓孔，而采用在螺栓所在区域表面施加压力进行近似等效。施加应力区域面积等于螺栓垫片的实际面积，根据式(2)计算压力，仿真中采用10 N·m对应的压强为标准工况。

2.1 有限元模型

图2为所研究的螺栓法兰结构。法兰中共12个螺栓，采用M6螺栓紧固，管道壁厚5 mm，材料为铝合金，铝合金参数与1.1节中相同；压电片型号为PZT-5H，尺寸为12 mm×3 mm×1 mm，对于螺栓法兰连接管的模型，仿真时采用4个压电片激励和4个压电片接收的方式，4个激励压电片在法兰的一侧，接收压电片在法兰的另一侧。由于同时激励4个压电片对设备要求较高，因此，仿真中采用激励单个压电片的方式。

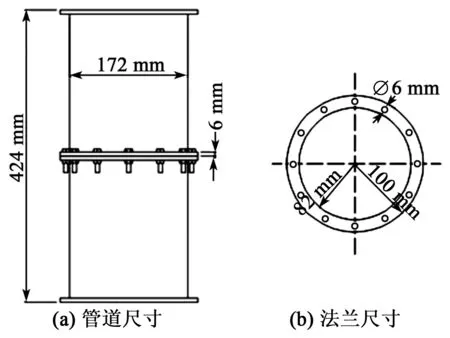
图2 螺栓法兰结构

采用商业有限元软件ANSYS建模，如图3所示。该模型的铝管采用SOLID185单元，压电片单元类型为SOLID5，法兰盘接触区域设置为面接触单元，设静摩擦系数为0.3。激励信号采用中心频率为70 kHz的5周期汉宁窗正弦调制信号，中心幅值为50 V。为准确模拟不同预紧力下的导波传播，采用2个载荷步进行计算，第一个载荷步为静力学分析，该载荷步内仅在螺栓处施加压力；第二个载荷步中，在压电片处施加电压激励，进行瞬态动力学分析。在瞬态动力学分析中，网格尺寸和时间步长的设置直接影响计算精度和计算时间耗费，即

(4)

(5)

式中：Δt为时间步长；Le为单元尺寸；fmax为波的最高频率；λmin为波的最小波长。因此，所建立的有限元模型中最大单元尺寸为2 mm，时间步长为1×10-3ms，瞬态动力学分析的时间历程设为0.2 ms。

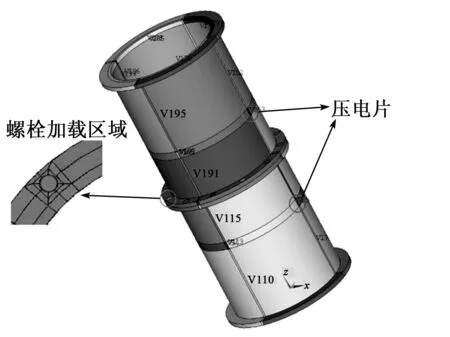
图3 三维螺栓法兰连接有限元模型及加载区域示意图

在仿真模型中，压电片位置编号和螺栓编号如图4所示。法兰一侧压电片为激励压电片，另一侧为接收压电片，法兰两侧对应位置的激励、接收压电片序号相同。

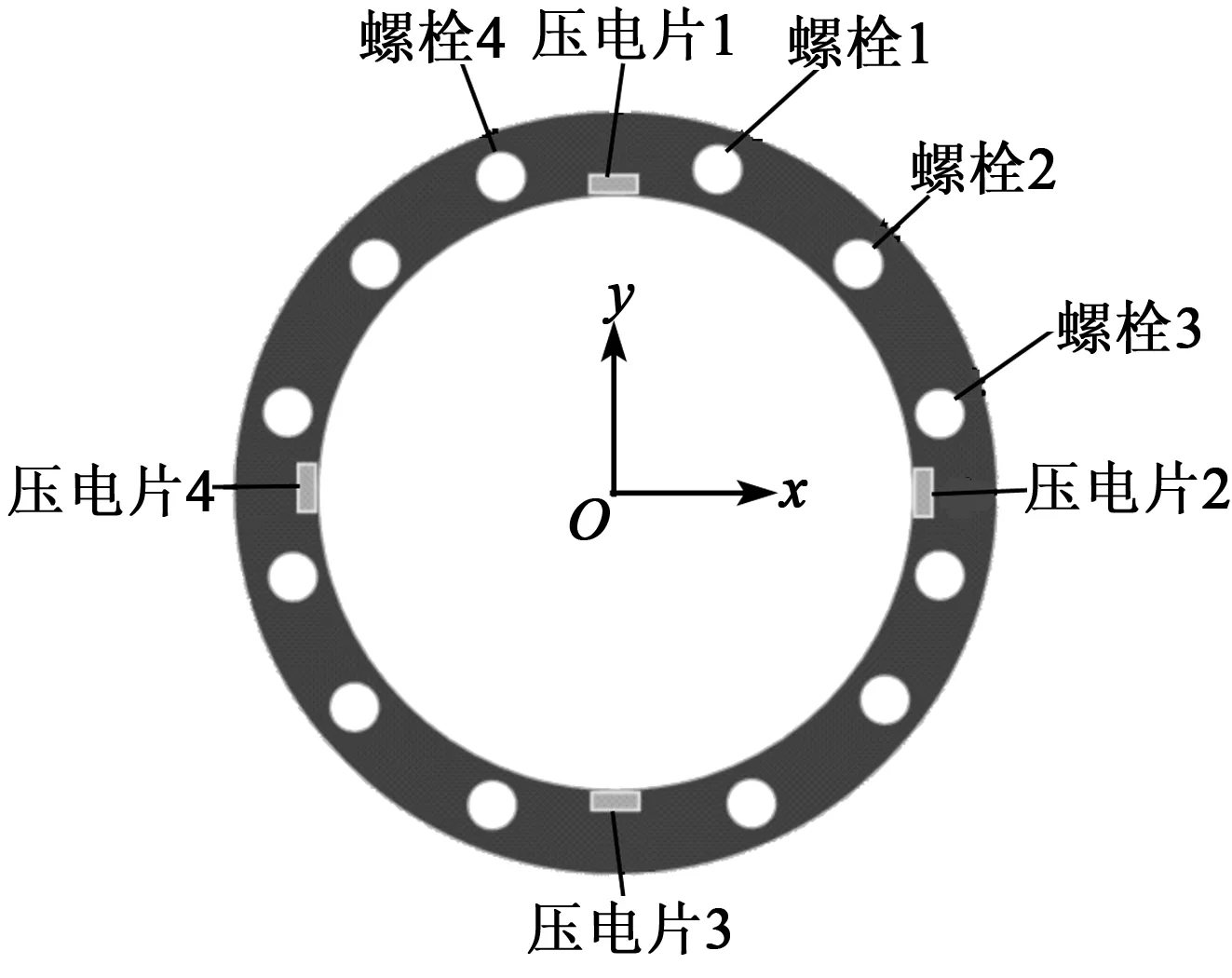
图4 压电片编号及螺栓编号示意图

2.2 仿真结果

2.2.1 扭矩整体变化对接收信号的影响

为研究压力对于导波信号的影响，首先激励压电片1，对比了12个螺栓分别同时在扭矩1 N·m和10 N·m时接收压电片1处导波响应信号的变化情况，仿真结果如图5所示。

由图5可看出，当12个螺栓全部处于标准扭矩10 N·m时，得到的响应信号幅值大于全部螺栓处于1 N·m的响应信号幅值。

2.2.2 拧紧指标随螺栓松动工况的变化

分析了不同位置螺栓松动后，超声导波信号的变化情况，为此设计了不同的仿真工况。

1) 仿真工况1：松动螺栓1。

2) 仿真工况2：松动螺栓1和2。

3) 仿真工况3：松动螺栓1和4。

此时对激励侧的压电片1进行激励，分别采集接收4个压电片上的响应信号，并进行对比，得到结果如图6所示。

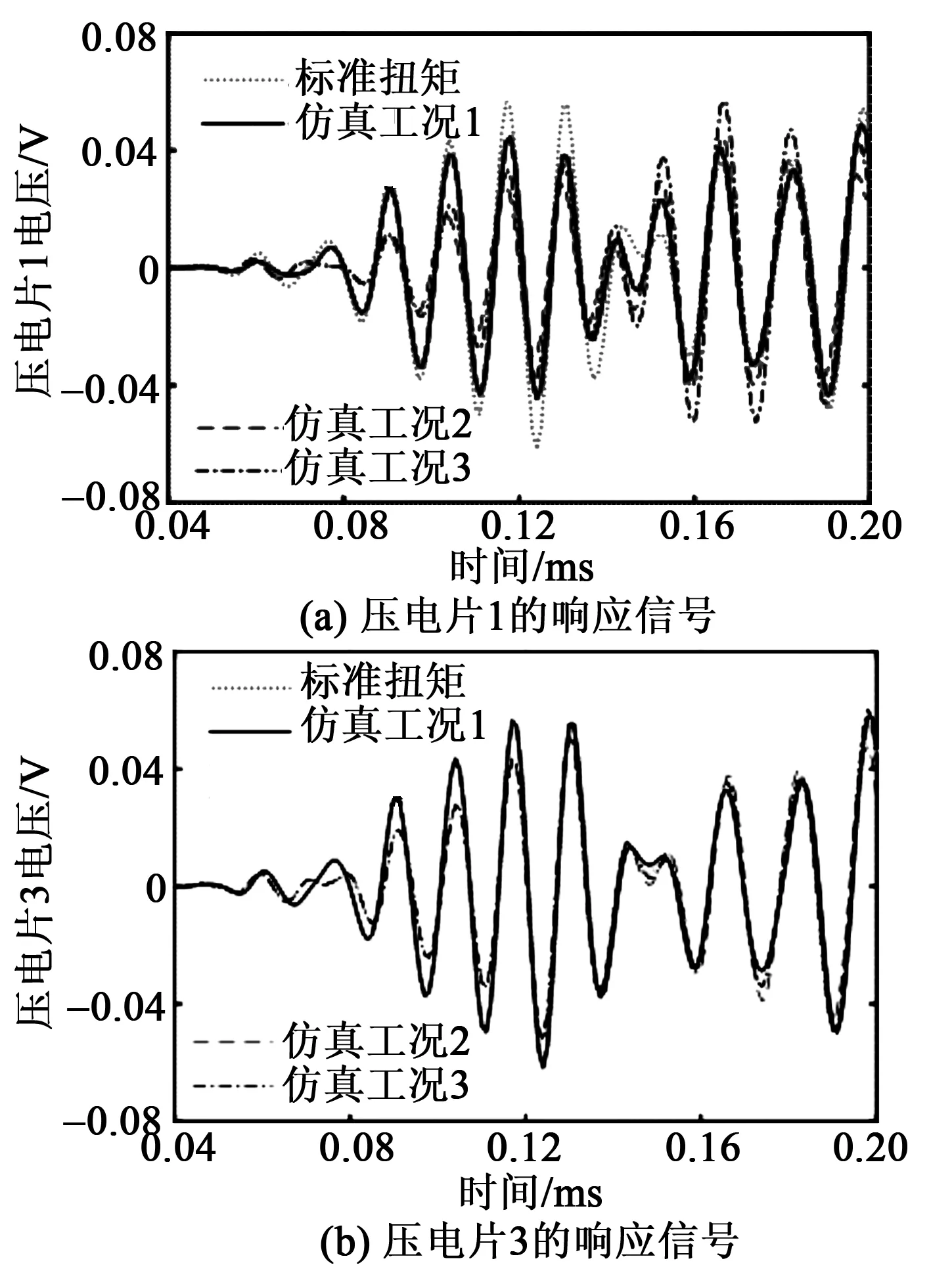
图6 不同仿真工况下压电片的响应信号

由图6(a)可看出，螺栓松动后，压电片1的幅值变化较大，在0.15 ms前螺栓松动后，响应信号幅值降低；在0.15 ms后螺栓松动后，响应信号幅值增加。同时可看出，松动2个螺栓时，信号变化更大。由图6(b)可看出，对于仿真工况1，压电片3的导波信号与标准扭矩下信号几乎无差别，这与压电片1的情况不同。其原因是压电片3与松动螺栓1距离很远，而压电片1与松动螺栓1距离很近，因而更灵敏。同时，对于仿真工况2、3，压电片3的信号也会变化，但变化幅值比压电片1小。

利用式(3)计算了上述仿真工况下的压电片1接受信号的均方根偏差指标，所得结果如图7所示。

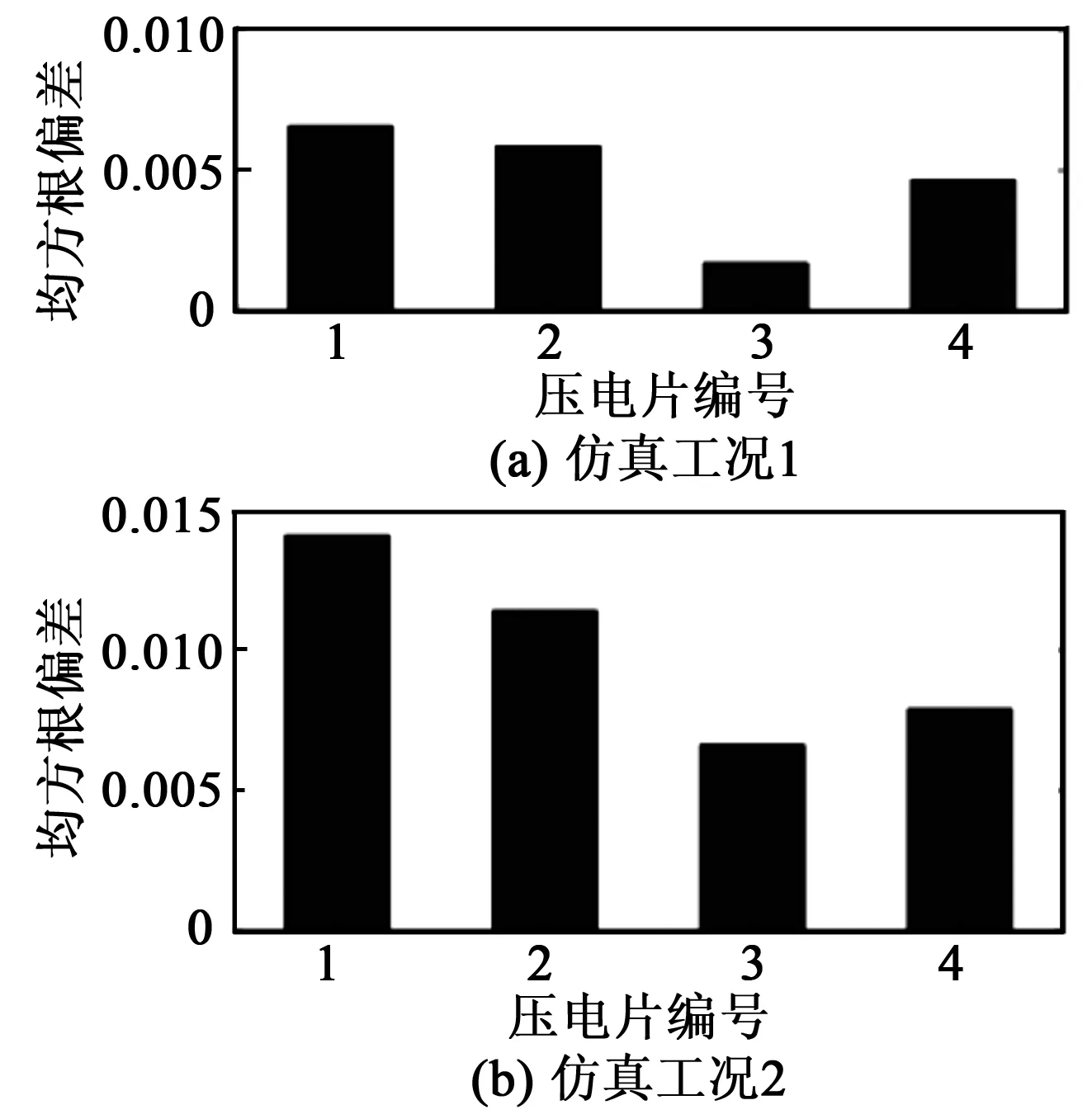
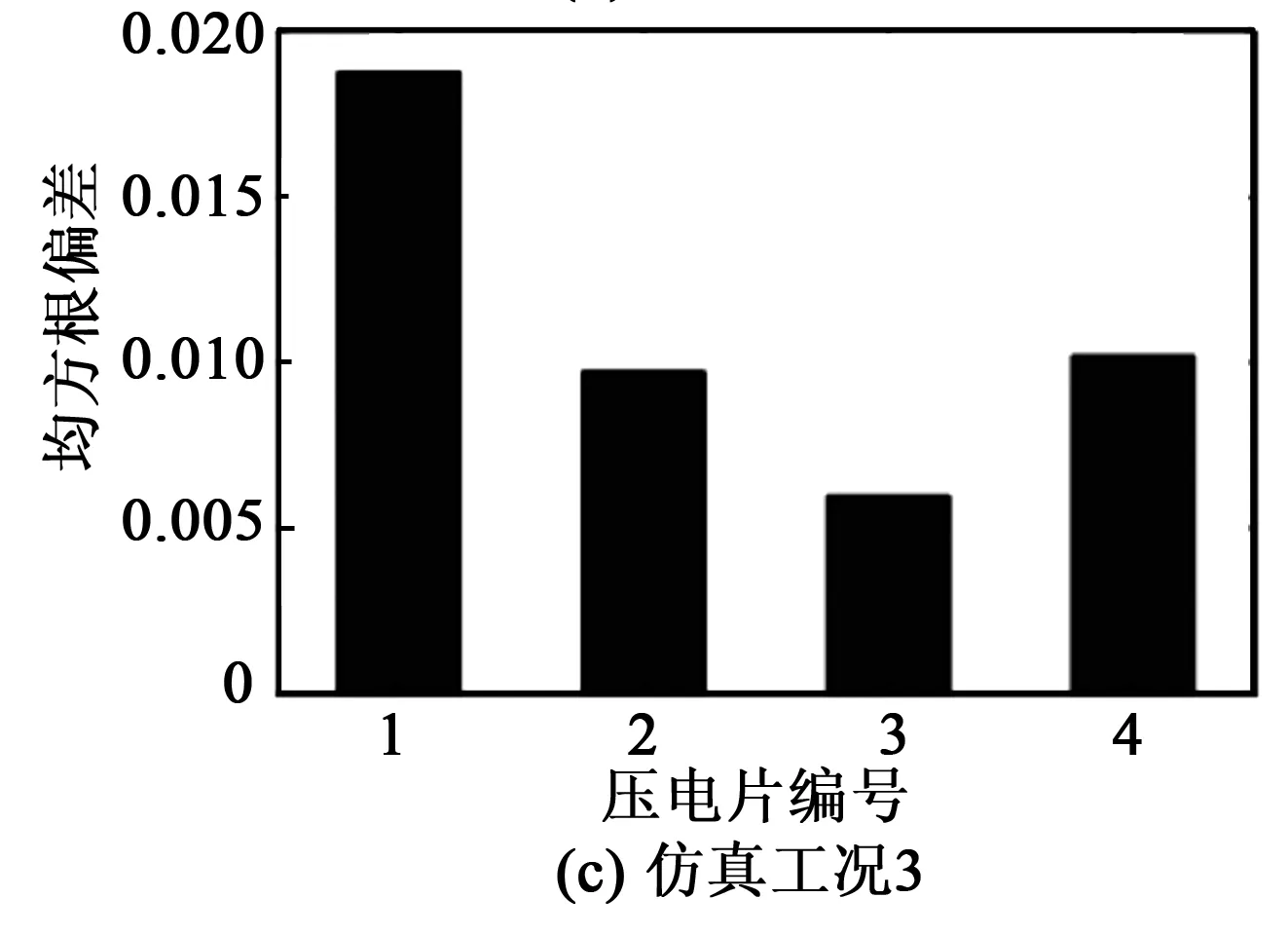
图7 压电片1接受信号的均方根偏差指标

由图7可看出，在4个接收压电片中，离松动螺栓最近的压电片1信号均方根偏差值最大，且其均方根偏差值随着松动螺栓个数的增加而增大。同时，与仿真工况2相比，仿真工况3中松动螺栓距离压电片1更近，因此，压电片1的均方根偏差值更大。由图还可看出，此时压电片2的均方根偏差值下降，这是因为松动螺栓4与压电片2的距离更远。3种工况中，压电片3的均方根偏差值一直是最小的，这是因为其距离松动螺栓最远。因此，通过上述4个压电片的均方根偏差幅值的变化情况可监测螺栓松动，并对松动位置做出初步判断。

3 实验验证

对所提出的螺栓松动监测方法进行了实验验证，以证明其可行性。

3.1 实验方案

实验采用的螺栓法兰结构尺寸与仿真中一致，管道材料为5052铝合金，法兰盘间同样采用12个5.6级的M6螺栓连接，采用的压电片与仿真中相同。由于实现4个压电片同时激励对设备要求过高，故实验时激励一个压电片，采集另一个筒上的4个压电片的响应信号。根据仿真结果，距离螺栓位置最近的压电片响应信号最灵敏。因此，实验中对压电片位置进行了调整，激励及接收压电片位置及螺栓编号示意图如图8所示。

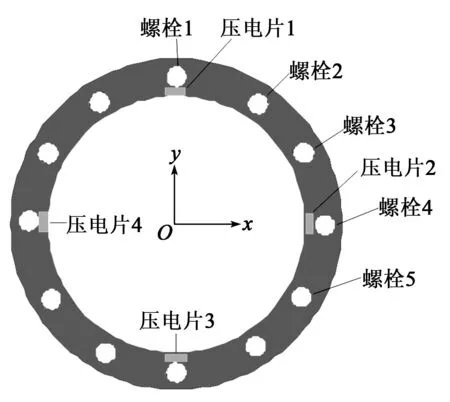
图8 压电片及螺栓编号

实验平台如图9所示，用NI USB-6366采集数据，采用PINTEK HA-400作为功放，同时利用LabVIEW控制输出激励信号，激励信号为中心频率70 kHz的5周期汉宁窗信号，经信号放大器放大施加于激励端，数据采集器的4个通道分别采集4个接收端压电片的信号，采样频率为2 MHz。实验中为了模拟自由边界条件，将试件放置于泡沫塑料上。

图9 实验装置及试件

实验中取4.8 N·m为标准扭矩，即标准工况。随后探究了单个螺栓松动及松动位置对于响应信号的影响，并对比了以下实验工况下的响应信号：

1) 实验工况0：无松动螺栓。

2) 实验工况1：松动螺栓2。

3) 实验工况2：松动螺栓1。

4) 实验工况3：松动螺栓2、3。

5) 实验工况4：松动螺栓5。

6) 实验工况5：松动螺栓4。

7) 实验工况6：松动螺栓4、5。

实验工况0中，将螺栓全部松动后重新拧到标准工况再采集响应信号。在实验工况1～3中，激励压电片1；在实验工况0、4～6中，激励压电片2。

3.2 实验结果与分析

在实验工况2时，提取了接收压电片1、2的响应信号，并将其与标准扭矩下进行了对比，结果如图10所示。由图可看出，实验工况2下接收压电片1、2的响应信号均有变化，而压电片1的变化更明显，这是由于压电片1与松动螺栓距离更近。另一方面，接收压电片1的响应信号部分波包幅值变大，而部分波包变小。

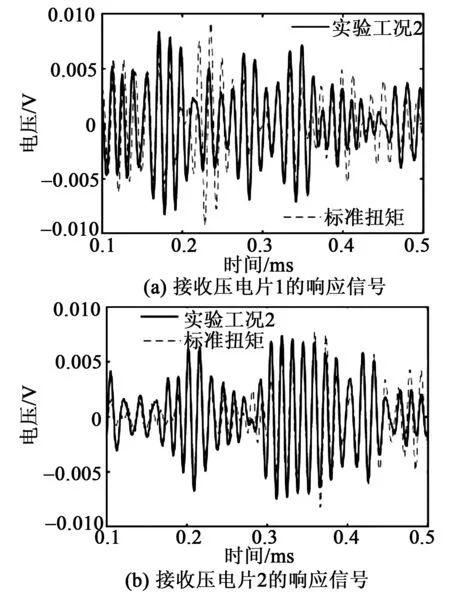
图10 实验工况2下压电片的响应信号变化

将实验工况1～6进行了3次重复实验，并利用响应信号前0.5 ms的数据，计算不同工况下每个压电片接收信号的均方根偏差指标。实验工况0～3的结果如图11所示，图中误差棒为标准差。

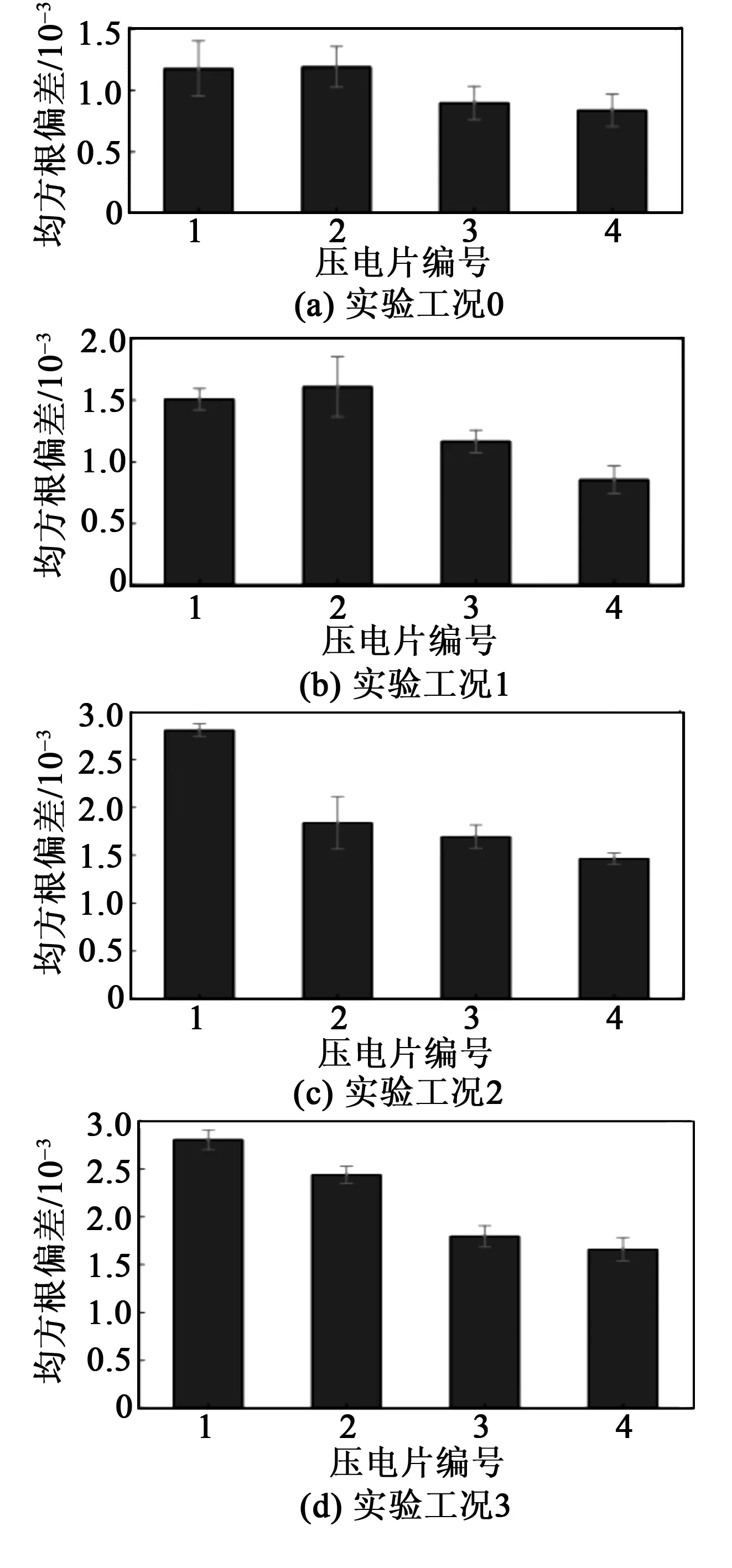
图11 不同实验工况下响应信号均方根偏差

由图11可看出，实验工况0的均方根偏差值小于其他工况。在实验工况1中，压电片1、2的均方根偏差值开始增加并高于压电片3、4。这是由于工况1中出现松动螺栓，且其位置在1、2压电片之间。实验工况2中，压电片1的均方根偏差值远高于其他压电片，这是因为实验工况2中接收压电片1与松动螺栓的距离最小。对于实验工况3，压电片1的均方根偏差值仍最大，压电片2的均方根偏差值有提高，主要原因是螺栓松动的数目增加。结果表明，压电片3、4的变化均较小，这是因为其距离松动螺栓较远。因此，根据上述4个压电片不同的均方根偏差值可判断松动工况。

在实验工况4～6中，由于松动螺栓的位置与接收压电片2位置最近，压电片2的均方根偏差值最大，且其变化模式与工况1～3一致。下面分别对比了4个接收压电片的均方根偏差值随着实验工况的变化情况，选取的实验工况是0、4～6，结果如图12所示。

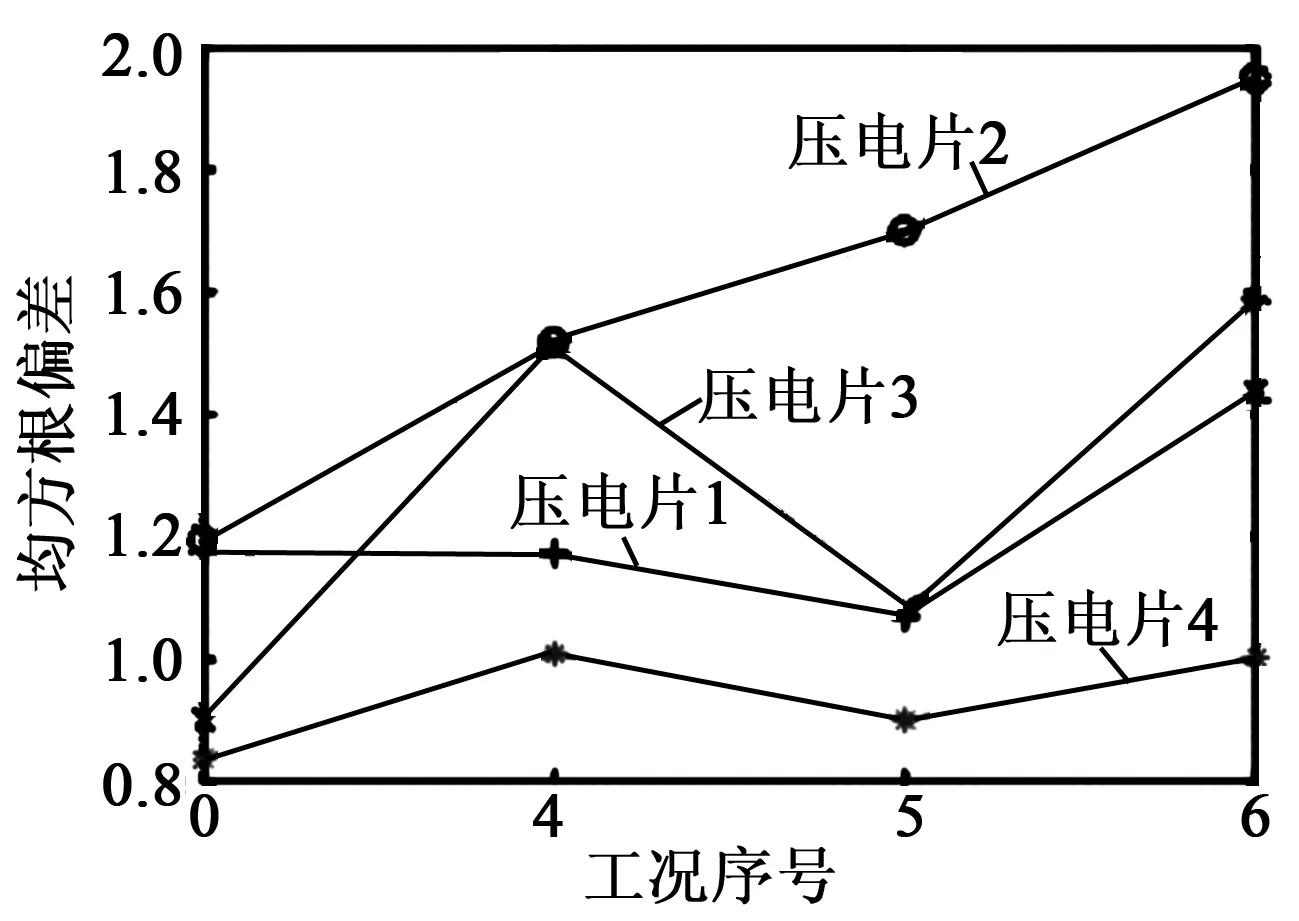
图12 压电片响应信号RMSD随工况的变化

由图12可看出，实验工况0时均方根偏差值均较小，而实验工况6中压电片1～3的均方根偏差值均较大，这是因为有2个螺栓松动。对于压电片2，均方根偏差值逐步增加，这是因为松动螺栓的位置与该压电片越来越近，且实验工况6中由1个螺栓松动变为2个螺栓松动。对于压电片3，在实验工况4、6，其均方根偏差值较大，这是因为这两个工况中松动的螺栓5与其距离较近。对于压电片4，由于松动螺栓与其距离最远，故其均方根偏差值变化很小。结果证明，当部分螺栓发生松动时，距离松动位置较近的压电片的响应信号计算得到的均方根偏差值较大；同时，根据均方根偏差值的分布模式可初步判断出松动螺栓的位置，验证了所提出方法的有效性。

4 结束语

针对法兰螺栓松动监测，本文提出利用超声导波信号的均方根偏差进行松动监测，并开展了数值仿真和实验验证。仿真和实验结果均表明，随着整体螺栓预紧力的下降，响应信号的幅值随之大幅减小。在1个或2个螺栓松动时，与松动螺栓距离最近的压电片响应信号最敏感，对应的均方根偏差值最大，同时随着松动螺栓的增加，所有压电片的均方根偏差值会有所增大。因此，通过均方根偏差值的大小及其分布可初步判断出松动螺栓的方位。