理论单位线曲线族数学公式的提出
2019-10-22宋雅坪房国忠郭希海
宋雅坪,房国忠,徐 峥,郭希海,孙 羽
(国家电网公司 东北分部,沈阳 110000)
1 概 述
洪水经验单位线是传统的洪水汇流预报方法[1],虽然方法简单,应用也很广泛,但预报时单位线的选取因人而异,预报结果的精度难以控制[2-3]。同时,经验单位线的分割与制作过程十分繁琐,难以达到理想完备的程度[4-5]。更重要的是经验单位线只能从已发生的洪水过程当中获得有限的(常见)洪水信息,对于未发生的罕见特大洪水的预报,由于缺少相应的外推单位线,极有可能存在洪峰预报严重偏小的重大安全隐患(即经验单位线缺乏外延递推性)[6-8]。能否找到一个理想完备的洪水径流单位线数学公式,使预报能够连续覆盖从极枯到极丰整个可能出现的土壤湿度状态(具有外延递推性),且其预报结果满足高精而稳定的要求,这是水文基础理论研究方面需要解决的基本问题[9]。
本文创立的理论单位线曲线族数学公式,为预报理论的实际应用提供了一种新的数学工具。期待该成果与产流预报模式相结合,在高精度预报模型中得到广泛的应用。
2 径流过程的图形描述
洪水径流过程是一个涨水段短、退水段很长的时序流量过程。当流域土壤干旱和降雨小时,产流少,洪水过程为矮胖型(洪峰涨幅小、洪水历时长);反之,当流域土壤湿润和降雨大时,产流多,洪水过程为尖瘦型(洪峰涨幅大、洪水历时短)。径流过程典型曲线见图1。

图1 径流过程典型曲线
3 洪水径流数学描述需解决的问题
3.1 寻求洪水径流过程Q-T曲线的数学公式
先要找到一个数学公式能够描述某一次洪水过程的完整形态。
3.2 验证洪水径流过程Q-T数学曲线族的代表性与完备性
在找到一个洪水径流数学公式的基础上,寻求一组洪水径流过程Q-T曲线族,其等分或非等分变化要与流域不同干湿程度的相应实际洪水单位线一一匹配,即理论单位线具有真实反映洪水径流丰枯变化的全过程(完备性),同时具有理论外延的合理性。
本文将试图通过指数函数的初等运算来解决这一复杂的汇流模式理论问题。
4 径流汇流模式的数学描述
4.1 径流过程的数学描述
洪水径流过程能否用数学公式来描述?如果能找到一个公式或初等函数来完整地反映洪水过程,不仅是一个十分有趣的数学练习,更重要的是可以通过后续预报应用研究,建立起一个更为复杂、完美的数学表达公式,乃至为水文学建立更为科学的理论打下基础。
洪水来水过程是一个涨水段相对较短、退水段相对较长的时序物理现象。这种形态的过程在其它领域也广泛存在,如通信的电话流量、公路交通流量过程等等。
由于许多水文物理量与指数函数e-at有密切联系,那么,由此推测洪水过程线的公式表达应当是以指数函数的初等运算为构成形式。果然,将两个不同退水系数的指数函数进行相减,就是一条很完美的洪水流量过程线。
Q(t,a,b)=A×(e-at-e-bt) 或
Q(t,a,b)=A×(exp(-at)-exp(-bt))
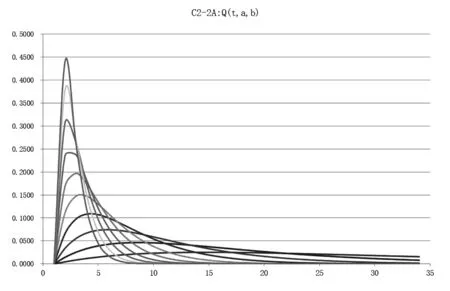
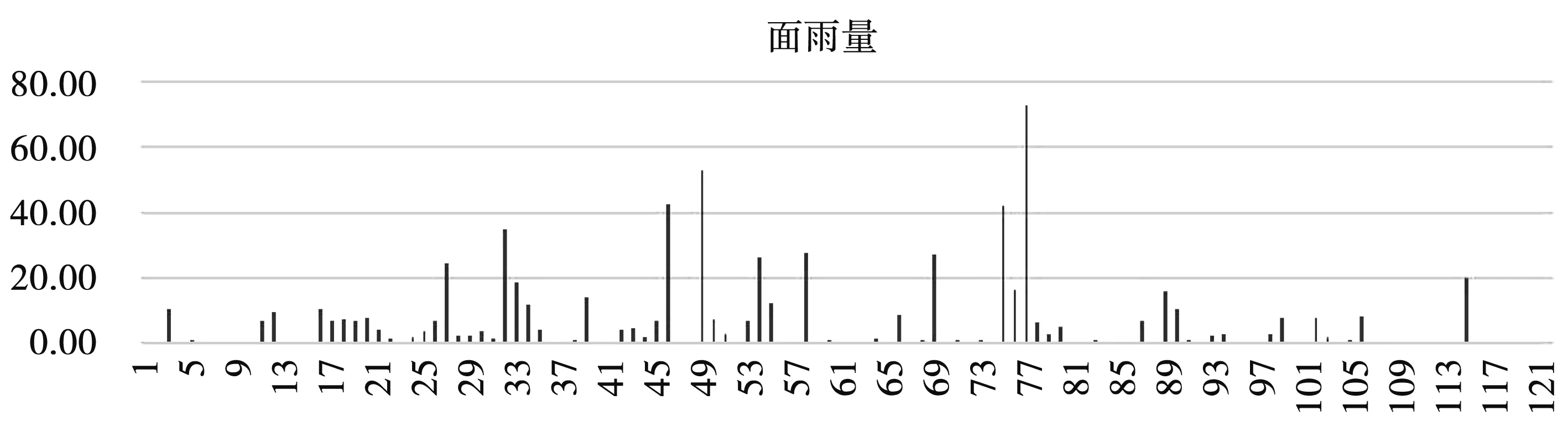
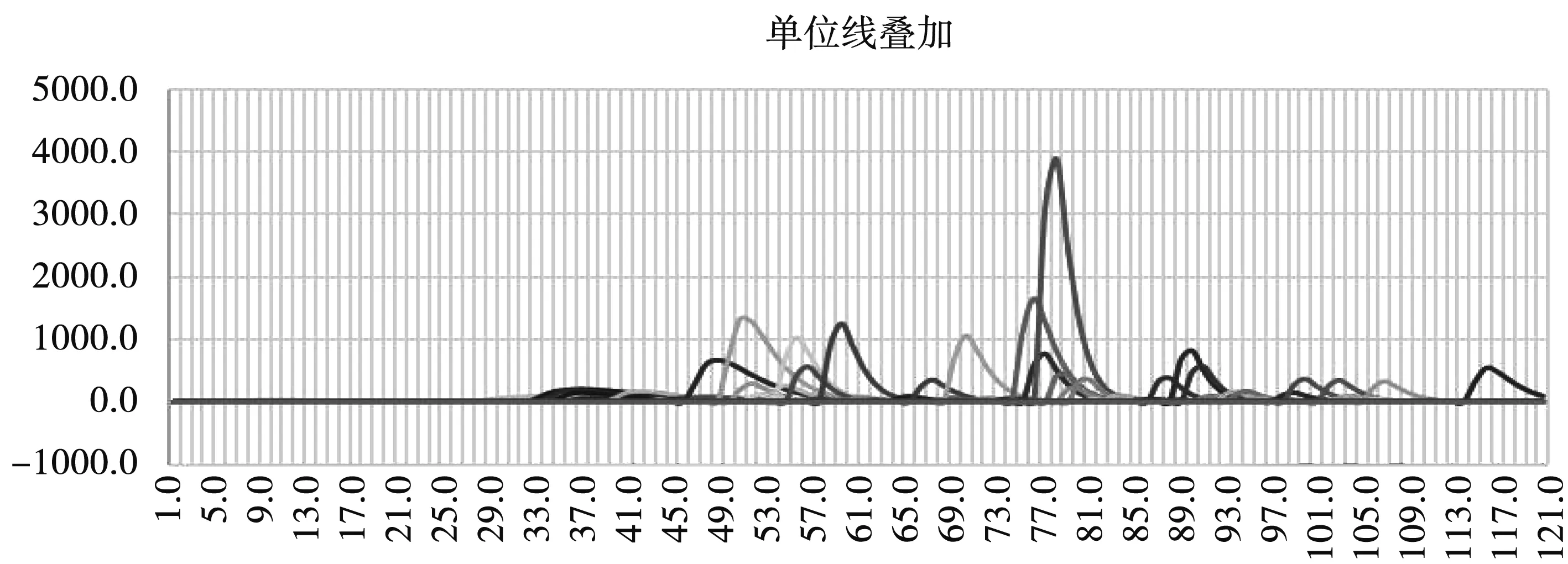
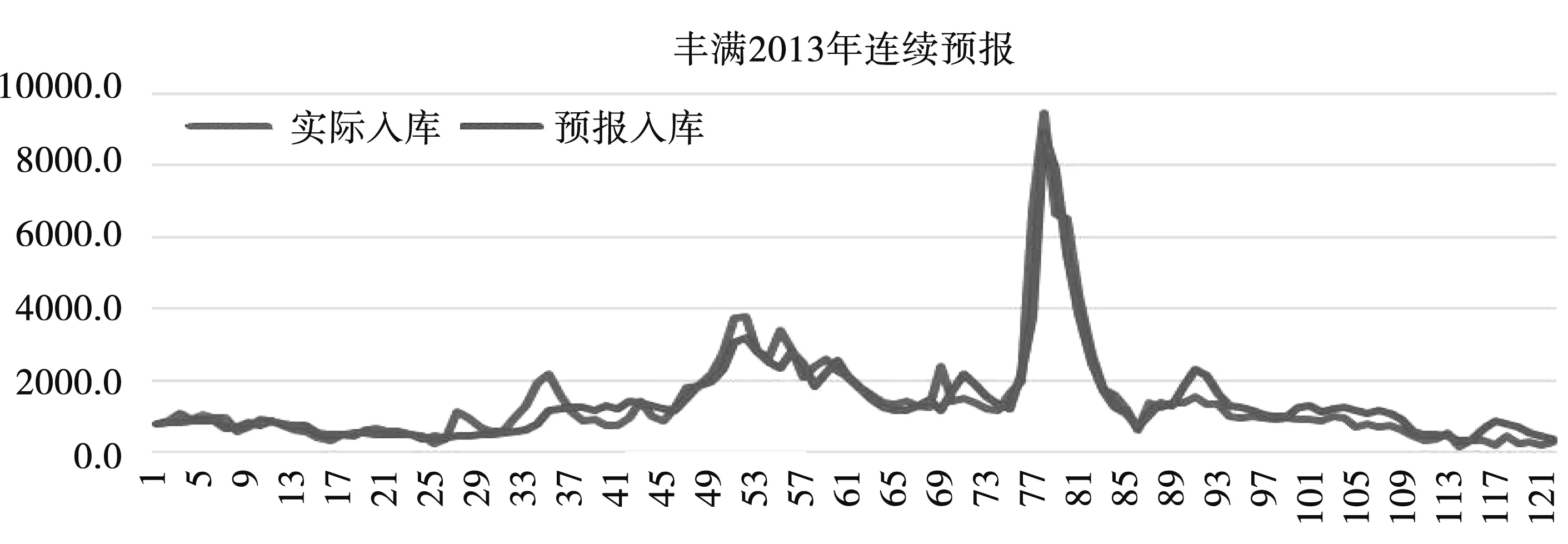
其中a 注:洪水曲线公式Q(t,a,b)=A×(e-at-e-bt) 的积分面积(洪水总量): 发现洪水径流过程Q-T曲线的数学公式后,工作仅仅是开始,还需要对洪水过程线公式进行数学处理,并解决Q-T曲线族的等分或非等分变化,目的是要让径流过程曲线族与实际流域不同干湿条件下的洪水单位线一一匹配,这样才有可能解决数学公式其代表的完备性与理论外延的合理性,其成果可以视为理论单位线。之所以称为理论单位线是因为Q-T曲线族的每条曲线的积分面积均为1。 通过反复试错后,合理选取不同的(a,b)参数,就可以完整地反映所有的洪水过程的变化趋势。理论单位线曲线族典型曲线见图2。 图2 理论单位线曲线族典型曲线 理论单位线曲线公式: Q(t,a,b)=1/(1/a-1/b)×(e-at-e-bt) 峰现时间: Tf=ln(a/b)/(a-b) 洪峰流量: Qf=ab/(b-a)×(e-aln(a/b)/(a-b)-e-bln(a/b)/(a-b)) 每条理论单位线的积分面积(t=0~∞): 每条理论单位线的计算面积(t=0~∞): s=∑Q(t,a,b)<1.0 注:曲线公式Q(t,a,b)=A×(e-at-e-bt)的面积S=A/(1/a-1/b)(A为常数) 基本假定:存在某一组参数(a,b)或(ai,bi)的理论单位线曲线族与径流系数(产流系数)可以建立唯一的对应关系,即曲线Q1,Q2,Q3,Q4,Q5,Q6,Q7,Q8,Q9,Q10分别对应径流系数为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0的洪水过程。基本假定能否符合实际,将通过后续预报应用和试错方法来检验。 给定不同的a,b参数就能得到不同的单位线,只要根据产流条件不同去合理调整a,b参数就能获得理想的洪水过程线,同时也就完成了相应的洪水径流汇流预报计算。 建模方式:先给定一组a,b参数的洪水预报标准模型,建立径流系数与理论单位线族的关系对应表;实际流域预报将根据径流系数(又称产流系数、出流系数)找到对应的单位线。同时,计算实际流域洪水历时与标准洪水历时的比值作为汇流标尺参数,进而计算时间标尺进行时标变换,代入理论单位线曲线公式即可完成洪水汇流预报计算。 如果预报结果不理想,重新给定另一组a,b参数的洪水预报标准模型,进行预报应用检验,直至预报结果完美。 洪水预报标准模型表见表1。 表1 洪水预报标准模型表 用退水段的平均退水系数代表该洪水曲线的退水系数(称为标准退水系数B标准),并与径流系数r建立回归关系。见图3。 本地退水系数:B本地=B标准^Tc 时间标尺:Tc=BT×DT/24 其中:DT为当地模型计算时段长(小时),汇流标尺BT为实际流域洪水历时与标准洪水历时的比值。 退水系数B与径流系数r关系见表2。 表2 退水系数与径流系数关系 退水系数仅用于预报模型开始时(预热段)的前期退水的计算,之后的连续预报则无此需求。 理论单位线曲线参数: ai=0.00875×(ri×Kqqt×10)^2+0.02375×(ri×Kqqt×10)+0.0175 bi=0.00875×(ri×Kqqt×10+1)^2+0.02375*(ri×Kqqt×10+1)+0.0175 si=100×(1/ai-1/bi) 其中:Kqqt各种汇流应用调节系数,用于洪水过程的局部修正(主要由人类活动影响确定)和洪水过程的整体修正(可由洪峰修正系数确定);ri为时段i的径流系数(又称产流系数、出流系数),是参数ai,bi的主要控制变量。 单位线汇流时段平均流量(m3/s): qij=0,当tj-ti<1 qij=-Ri/0.000864×100/si×TC×((exp(-ai×(tj-ti)×TC)-exp(-ai×(tj-ti)×TC))/ai/TC-(exp(-bi×(tj-ti)×TC)-exp(-bi×(tj-ti)×TC))/bi/TC),当tj-ti>=1 其中:Ri为时间标尺TC、时段i的产流量(又称径流总量),108m3。 理论单位线预报应用实例:将理论单位线曲线族模型应用到丰满2013年连续洪水预报当中,预报曲线与实际曲线符合程度较高,预报结果见图4-图6。 图4 丰满流域面雨量 图5 单位线曲线族叠加曲线 图6 丰满2013年连续洪水预报曲线 1) 洪水径流数学描述——理论单位线曲线族数学公式的提出,为水文基础理论在汇流方面的研究提供了一种新的完备理论汇流模式。 2) 理论单位线曲线族数学公式及其标准结构设计具备外延递推的合理性,通过理论单位线曲线族与径流系数之间建立恰当的关系,可以解决复杂的流域径流的汇流预报问题。 3) 由于理论单位线族具备丰枯全过程连续覆盖的洪水汇流计算特性,从而有望与其它高精产流预报模式相结合,为后续建立精确的产-汇一体预报模型提供坚实的理论算法,达到自动选配单位线,实现高精、高效预报的目的。4.2 理论单位线曲线族数学公式

5 理论单位线应用建模(汇流理论模式)
5.1 洪水预报标准模型表(理论单位线族)
5.2 确定退水系数B和时间标尺Tc

5.3 确定理论单位线参数
5.4 计算单位线汇流时段平均流量
6 结 论
