连续微弯弯道水流结构试验研究

2019-10-22卢翔，李觅

水利科技与经济 2019年9期

卢翔，李觅

(湖南省水利水电勘测设计研究总院，长沙 410007)

弯曲型河道是组成河流的基本单元之一，对防洪、航运及桥梁工程有着重要影响。自1870年J.Thompson在弯道水槽实验中发现螺旋流以来，国内外不少学者通过实地观测、数学模型计算及物理模型试验等方式从不同角度对弯道水流特性进行研究，取得了大量的成果。实地观测方面，Leeder等[1]从天然河流弯道中的水流分离现象入手，提出弯曲半径与河宽的比值及弗洛德数作为预测水流分离发生的经验判断标准。数学模型方面，杨燕华等[2]基于雷诺方程和有限体积法建立连续弯道水流的三维数学模型，研究弯道水流纵向流速剖面的变化，给出流速剖面沿程和横向的变化趋势；Stoesser等[3]采用不同数值方法模拟弯道水流结构，通过实测资料进行验证，对不同方法模拟下的流速和壁面切应力分布进行比较分析。物理模型方面，陈启刚等[4]利用PIV系统在两种不同试验方式配合下重构弯道水流的三维平均流场，对弯道水流的平均运动规律进行研究；Blanckaert等[5]根据模型试验数据对弯道环流的影响因素进行分析，指出湍流是产生凹岸弱环流的原因；刘月琴等[6]采用ADV对弯道水流紊动特性进行试验研究，根据试验数据探讨弯道水流的紊动机理并分析弯道水流的紊动特性。这些研究有一个共同特点，即研究对象为曲折系数(弯道实际流向长度与弯道起止点直线距离之比)较大的单个弯道，这种弯道水流具有主流位于凹岸侧，断面形成表层水流指向凹岸、底层水流指向凸岸的大尺度横向环流等特点。

天然顺直河道的枯水河槽通常表现为连续微弯弯道的形式，曲折系数较小，枯水和平滩流量下河道水流流动类似于弯道水流。以往大多数学者将重点放在较大曲折系数的单弯道水流特性研究中，以连续微弯弯道为研究对象的成果较少见。本文试验采用连续微弯弯道的概化模型，从纵向垂线平均流速、水流动力轴线、纵向和横向流速分布及环流强度等方面较为系统研究这种弯道的水流结构。

1 试验条件及方法

1.1 试验条件

试验模型平面布置见图1。

图1 试验水槽系统布置Fig.1 Layout of the flume experiment system

试验水槽全长23 m，宽1 m，其中试验段长13 m。试验段分为进口直线段(0～3 m)，弯道段(3～11 m)和出口直线段(11～13 m)。弯道段由8段等尺度圆弧形弯段反向连接而成。弯道中心线半径为0.86 m，曲折系数K为1.067，弯道底坡降为0.5‰。模型过水断面为梯形，尺寸见图2。

图2 模型断面尺寸Fig.2 Size of the model cross-section, cm

1.2 试验方法

试验采用两组流量、水位组合，分别代表枯水和平滩两种典型工况。试验工况见表1，其中水深、水面宽度和水面半径均为沿程平均值。水槽边壁沿水流方向(X方向)从300 cm开始，间隔50 cm垂直于流向布设一个流速测量断面，全程共布设15个流速测量断面，记作1#-15#断面。流速测量采用日本JFE公司研制的ACM2-RS型二维电磁流速计，测量精度为±0.5 cm/s，测量频率为20 Hz。流速测量从水面以下2 cm开始，沿垂向(Z方向)间隔1 cm及河宽方向(Y方向)间隔4 cm设置测点。为尽量减少误差，每个测点至少记录600个瞬时值左右，采样时间内紊流至少经过了一个周期，对其求平均值得到各测点的时均纵向、横向流速。工况一和工况二分别布置900和1 560个测点，测点布设密度适中，能较好反映水流结构。

表1 试验工况参数Tab.1 Parameters of experiment conditions

2 试验结果及分析

2.1 纵向垂线平均流速

纵向垂线平均流速平面分布图见图3。从图3上看出，两个工况纵向垂线平均流速分布较为相似，弯顶处水流高流速区均位于凸岸附近，凸岸侧的流速梯度明显大于凹岸侧；过渡段水流高流速区基本位于断面中心区域，相邻弯顶断面左右岸流速梯度呈规律性交替变化。说明水流进入连续微弯弯道后，主流向凸岸方向偏移，在过渡段处逐渐居中，然后在下一个弯道重新向凸岸偏移。两个工况中，弯顶断面凹岸近壁处均出现反向的流速，即发生水流分离现象，且工况二现象较工况一更为明显，这与弯道中水流分离现象通常出现在凸岸侧的情况不同[7-8]。这是由于本试验弯道曲折系数较小，接近于直道，水流基本沿直线前进，主流靠近凸岸侧，因此易在凹岸侧出现水流分离现象。而以往的试验及天然弯道的曲折系数较大，水流受到边界的约束作用较明显，主流进入弯道后逐渐由凸岸摆向凹岸，凸岸附近区域变为低流速区，水流流速降为零乃至负值。

图3 纵向垂线平均流速平面分布Fig.3 Plain layout of depth-averaged longitudinal velocity

2.2 水流动力轴线

水流动力轴线又称为主流线，指沿程各断面最大纵向垂线平均流速所在点的连线。图4为河道在两种工况下主流线变化情况。相较于弯道主流线大弯曲度及偏向凹岸侧的一般特点，连续微弯弯道主流线基本位于中心线附近，水流对凹岸顶冲的位置不明显。由于工况二流量大于工况一，水流的惯性力更大，其主流线摆动幅度小于工况一。

图4 水流动力轴线对比Fig.4 Comparison of fluid dynamic axis

2.3 纵向流速分布

纵向流速垂线分布选取槽内的垂线进行分析，该位置水深最大，测点数据较多具有代表性。以工况二的8#、9#及10#断面为例，分析纵向流速垂线分布横向变化，并加入工况一的8#断面进行对比，见图5，S为垂线至断面左岸顶点的距离(图2)。

由图5看出，工况二位于弯顶的8#断面和10#断面纵向流速变化规律基本一致：凸岸侧垂线流速分布接近于对数分布，测点流速沿水深方向变化较小；凹岸侧垂线流速沿水深方向先增大后减小，最大流速点始终位于z/H=0.25附近，整体呈现“凸肚”形。工况一断面纵向流速分布和工况二近似，凹岸侧最大流速点位置高于工况二。Blanckaert等[9]通过实验和理论分析指出，横向环流引起的横向对流动量输移是影响纵向流速分布的主要因素，它使得床面附近的流速增大，平顺了纵向流速沿垂线方向的分布。张红武等[10]认为弯道中纵向流速剖面与环流强度直接相关，环流强度越大纵向流速剖面变形随之加大。由此可见，凹岸侧流速最大点靠近底部，流速垂线分布偏离对数分布的现象应与该侧形成较为明显的横向环流有关。

图5 纵向流速垂线分布横向变化Fig.5 Lateral variation of vertical distribution of longitudinal velocity

2.4 横向流速分布

弯道水流显著特点为弯道离心力和静水压力差共同作用产生的横向和垂向流速，即形成弯道环流。同上选取工况二的8#、9#及10#三个典型断面分析横向流速分布，并加入工况一的8#断面进行对比，见图6。

图6中，平滩工况中断面横向流速明显小于纵向流速，弯顶断面呈现双环流结构，其中凹岸侧的环流靠近水面，凸岸侧的环流靠近床面，凹岸侧水流横向流速略大于凸岸侧，这与数值模拟的结果相符[11]。枯水工况的断面横向流速小于平滩工况，说明顺直微弯弯道中流量越大，横向环流越明显。弯道中形成了正向的凸岸主环流和逆向的凹岸次生环流，这与通常弯道中表层水流指向凹岸、底层水流指向凸岸的单环流现象有着显著差异。

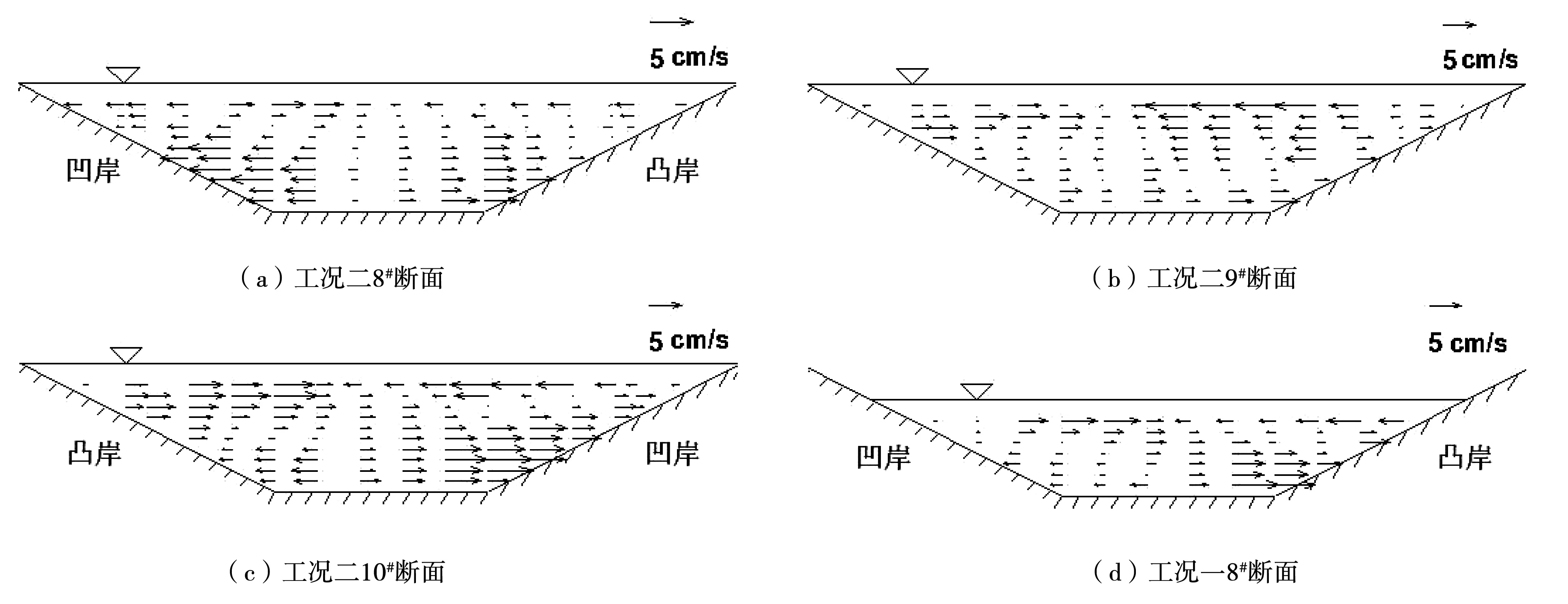
图6 断面横向流速分布Fig.6 Distribution of transverse velocity in the cross-section

Blanckaert等[5]在急弯模型试验中同样发现了类似现象，其试验中凸岸处形成的主环流明显强于凹岸处形成的次生环流(图7)，而本试验中弯顶断面形成的两个环流尺度显然更为接近，这推测原因为本试验弯道的曲折系数较小，水流受到边界的约束作用较弱，因此弯顶断面形成了两个大小更接近的弱环流。此外，连续弯道中下游弯道的环流通常受到上游弯道环流的影响，两弯道过渡段中往往残存着上游弯道的环流，见图6(b)，这是连续弯道和单弯道水流结构的明显区别。

图7 Blanckaert等[5]弯道试验断面横向流速分布Fig.7 Distribution of transverse velocity in a cross-section of Blanckaert’s flume experiment

2.5 环流强度

Blanckaert等[12]从纵向二维垂向平均动量方程出发，将不同点的速度分解为所在垂线平均值加上差值，并采用de Vriend[13]提出的简化三维Navier-Stokes方程解，定义垂线环流强度如下：

(1)

式中:〈〉为垂线平均值；vn为测点横向流速；Un为横向垂线平均流速；Us为纵向垂线平均流速；H为断面平均水深；R为中心线曲率半径。式(1)综合考虑了横向和纵向流速以及其它水力因素，同时取垂线平均值，能够反映出不同垂线的环流强弱。

利用式(1)计算工况一和工况二的6#-12#断面槽内的垂线环流强度，结果见图8。由图8可以看出，工况一和工况二垂线环流强度变化规律相似，工况一环流强度略小于工况二。整体而言，左岸侧及右岸侧各垂线环流强度沿流向分布相似，两岸分布规律相反，断面中心线处垂线环流强度维持较小值。弯顶断面(6#、8#、10#和12#断面)凹岸侧垂线环流强度大于凸岸侧，且更靠近边壁的垂线环流强度更大，这印证了凹岸侧纵向流速垂线分布偏离对数分布与该侧形成更为明显的环流有关，同时说明环流强度的大小受到边壁的影响。断面环流强度峰值沿程基本保持不变，说明连续弯道中各断面形成近似的稳定环流。