立足核心知识 增强应用意识
2019-10-22文康叶红
文康叶红
第一章 一元二次方程
领 衔 人:诸士金
组稿团队:南京市秦淮区初中数学骨干教师孵化第六组
一元二次方程作为整式方程家族里重要的一员,是继一元一次方程、二(三)元一次方程组、可化为一元一次方程的分式方程后,又一个常见的方程模型。二(三)元一次方程组可以看作是对一元一次方程在“元”上的推广,那么一元二次方程可以看作是对一元一次方程在“次”上的推广。
在现实生活中,许多问题中的数量关系都可以抽象为一元二次方程,方程模型丰富多彩。一元二次方程是以前学习的方程知识的延续和深化,它在现实生活以及数学中同样有着广泛的应用。我们知道方程模型的研究路径一般是“概念——解法——应用”,一元二次方程也不例外,下面对本章的知识进行梳理,具体如下:

由这个知识框架我们可以知道,从实际问题中抽象出数量关系、列出一元二次方程、求出方程的解,解决实际问题是学习一元二次方程这一章的主线。因此,我们需要明确学习目标,具体如下:
1.理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程;
2.会用一元二次方程根的判别式判别方程是否有实根和两个实根是否相等;
3.了解一元二次方程的根与系数的关系;
4.能根据具体问题的实际意义,检验方程的解是否合理;
5.能根据具体问题中的数量关系列出方程,体会方程是刻画现实世界数量关系的有效模型。
了解学习目标后,我们结合中考真题,一起来看一下一元二次方程这一章中的核心知识。
核心知识1:解系数是数字的一元二次方程
例1(2018·徐州)解方程:2x2-x-1=0。
【解析】想要求方程的解,需要观察这个方程的结构。经判断这是一个一元二次方程,二次项系数是2,一次项系数是-1,常数项是-1,我们可以选择配

例2 (2019·扬州)一元二次方程x(x-2)=x-2的根是 。
【解析】观察这个方程的结构,发现等号两边都有x-2,可以移项为:x(x-2)-(x-2)=0,选择因式分解法(提取公因式)来求解,或者将这个方程化成一般式x2-3x+2=0,选择公式法或配方法来解这个一元二次方程。
【答案】x1=2,x2=1。
【总结】这两题考查了一元二次方程的解法。一元二次方程的解法,包括配方法、公式法和因式分解法等,是一元二次方程这一章的重点内容之一。解一元二次方程的基本策略是降次,即通过配方、因式分解等,将一个一元二次方程转化为两个一元一次方程来解。具体地,根据平方根的意义,可得出x2=p和(x+n)2=p的解法。通过配方,我们可以将一元二次方程转化为(x+n)2=p的形式再求解;一元二次方程的求根公式x=方法或者公式法来解这个一元二次方程。,就是对方程ax2+bx+c=0(a≠0)配方后得出的。
核心知识2:判别方程是否有实根和两个实根是否相等
例3 (2016·宿迁)若一元二次方程x2-2x+k=0有两个不相等的实数根,则k的取值范围是 。
【解析】由题目中信息“方程x2-2x+k=0有两个不相等的实数根”可联想到,当b2-4ac>0时,有两个不相等的实数根。因此 b2-4ac=(-2)2-4×1×k=4-4k>0,即k<1。
【答案】k<1。
【总结】本题考查的是一元二次方程的根的情况,利用一元二次方程根的判别式判别方程是否有实根和两个实根是否相等。我们只要掌握如下知识,这一类问题便可迎刃而解。
一元二次方程ax2+bx+c=0(a≠0)的根的情况如下:
当b2-4ac>0时,有两个不相等的实数根;
当b2-4ac=0时,有两个相等的实数根;
当b2-4ac<0时,没有实数根。
核心知识3:一元二次方程的根与系数的关系
例4 (2019·盐城)设x1、x2是方程x2-3x+2=0的两个根,则x1+x2-x1x2=___。
【解析】已知一元二次方程x2-3x+2=0的二次项系数a=1,一次项系数b=-3,常数项c=2,由一元二次方程的根与系数的关系可得x1+x2-x1x2=3-2=1。
【答案】1。
【总结】本题考查了一元二次方程的根与系数的关系,此为选学内容。一元二次方程的根与系数有如下关系:
方程ax2+bx+c=0(a≠0)的两个根是x1、x2,则它们之间有如下关系:

核心知识4:用一元二次方程解决实际问题
例5 (2016·泰州)随着互联网的迅速发展,某购物网站的年销售额从2013年的200万元增长到2015年的392万元。求该购物网站平均每年销售额增长的百分率。
【解析】平均变化率问题(以增长为例)中常用的数量关系是:“变化前的量+增长的量=增长后的量”“增长的量=变化前的量×增长率”。将这两个数量关系合起来可表示为:变化前的量×(1+增长率)=增长后的量。如果设平均增长率为x,2013年的年销售额为200万元,2014年的年销售额为200×(1+x)万元,2015年的年销售额为200×(1+x)×(1+x)万元,即200(1+x)2万元,根据“从2013年的200万元增长到2015年的392万元”,即可列出方程。
解:设该购物网站平均每年销售额增长的百分率是x。
根据题意,得200(1+x)2=392。
解这个方程,得x1=0.4,x2=-2.4(不合题意,舍去)。
答:该购物网站平均每年销售额增长的百分率是40%。
【总结】平均变化率问题的关键是理解变化率和变化量的区别,进而正确理解经过1次、2次变化,数量的变化量和变化率的表示。可设变化前的量为a,变化后的量为b,平均变化率为x,则经过2次变化后的数量关系可表示为a(1±x)2=b。
例6 (2018·盐城)一商店销售某种商品,平均每天可售出20件,每件盈利40元。为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件。
(1)若降价3元,则平均每天销售数量为_______件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
【解析】问题中涉及的数量关系较多,如:“降价前每件商品的利润×降价前每天的销售量=降价前总利润”“降价后每件商品的利润×降价后每天的销售量=降价后总利润”“降价前每件商品的利润-每件商品的降价数=降价后每件商品的利润”“降价前每天的销售量+2×降价数=降价后每天的销售量”等。
我们可以借助列表的形式分析其中的数量关系,其中设每件商品降价x元时,该商店每天销售利润为1200元,则可表示如下表:
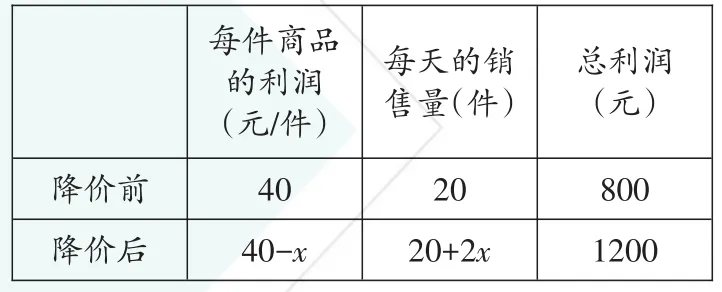
800 1200每天的销售量(件)总利润(元)降价前降价后每件商品的利润(元/件)40 40-x 20 20+2x
解:(1)26;
(2)设每件商品降价x元时,该商店每天销售利润为1200元,则平均每天销售数量为(20+2x)件,每件盈利为(40-x)元,且40-x≥25,即x≤15。
根据题意可得(40-x)(20+2x)=1200,
整理得,x2-30x+200=0,
解得x1=10,x2=20(不合题意,舍去)。
答:每件商品降价10元时,该商店每天销售利润为1200元。
【总结】一元二次方程是刻画现实世界中某些数量关系的有效数学模型。在运用一元二次方程分析、表达和解决实际问题的过程中,利用表格可以帮助我们分析其中的数量关系,建立数学模型解决实际问题。
此外,我们还要根据具体问题的实际意义,检验方程的解是否合理。
总之,对于一元二次方程的学习,我们在解一元二次方程时,抓住“降次”这一基本策略,在解决实际问题时,利用表格或者线段示意图分析题意,寻求数量关系,尝试建立方程模型解决问题,增强数学应用意识,努力做到化繁为简、化难为易、有的放矢。
