坐标系与参数方程解题策略

秦坤超 第一中学 河北省衡水市

一、参数方程、极坐标方程与普通方程的互化

对于极坐标与直角坐标的相互转化而言，直角坐标化为极坐标方程比较容易，只需将公式x=ρcosθ，y=ρsinθ直接代入并化简即可；而极坐标方程化为直角坐标方程则相对困难一些，解此类问题，常用方法有代入法、平方法等，还经常会用到同乘(或除以)ρ等技巧.

在将曲线的参数方程化为普通方程时，不仅仅是把其中的参数消去，还要注意 x、y 的取值范围，同时在消去参数的过程中一定要注意普通方程与参数方程的等价性.常见的消参数法有：代入消元(抛物线的参数方程)、加减消元(直线的参数方程)、平方后再加减消元(圆、椭圆的参数方程)等.而对于含三角函数的参数方程，经常使用的公式为sin2α＋cos2α＝1.在将曲线的参数方程化为普通方程的过程中，一定要注意参数的范围，确保普通方程与参数方程等价，否则很容易因为忽略参数方程中的某些限制条件而失误.

应该注意的是，极坐标方程与参数方程之间不能直接互化，必须以普通方程为桥梁，即将极坐标方程转化为普通方程再转化为参数方程，或将参数方程转化为普通方程再转化为极坐标方程，要注意普通方程与参数方程的等价性.

【例1】已知曲线C的极坐标方程为ρ＝2cos θ，以极点为原点，极轴为x轴的正半轴建立直角坐标系，则曲线C的参数方程为___________.

【解析】由 ρ＝ 2cos θ知，ρ2 ＝ 2ρcos θ

二、参数方程的应用

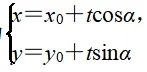
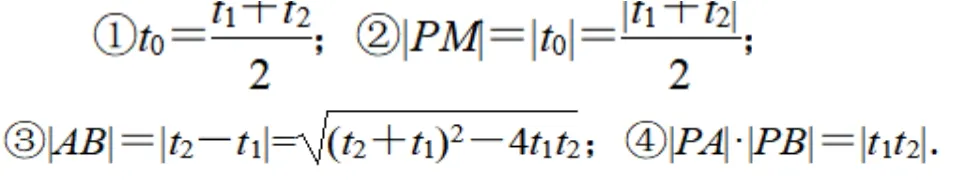
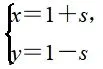
三、极坐标方程及其应用

求曲线的极坐标方程的步骤为：(1)建立适当的极坐标系，设P(ρ，θ)是曲线上任意一点；(2)由曲线上的点所适合的条件，列出曲线上任意一点的极径ρ和极角θ之间的关系式；(3)将列出的关系式进行整理、化简，得出曲线的极坐标方程.

由直角坐标方程化为极坐标方程，其方法就是把x＝ρcos θ，y＝ρsin θ代入方程，根据三角函数公式整理．

【例3】在直角坐标系xOy中，直线C1：x＝-2，圆C2：(x-1)＋(y-2)＝1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系.

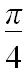
【解析】：(1)因为 x＝ ρcosθ，y＝ ρsinθ，所以 C1的极坐标方程为 ρcosθ＝-2，

C2的极坐标方程为 ρ2-2ρcosθ-4ρsinθ＋ 4 ＝ 0.