基于NLS方程的畸形波演化规律研究
2019-10-21罗春莲

摘 要:畸形波具有短暂性和偶然性的特征,导致畸形波实测数据较少,畸形波的机理及影响因素仍然不明确。本文针对有限水深Peregrine呼吸子解畸形波的生成及演化进行了相关研究。
关键词:畸形波;NLS方程;Peregrine呼吸子解
0 引言
过去,有限水深畸形波的规律研究多从边带不稳定性出发(Stokes波对于缓慢调制的周期性扰动是不稳定的),如:Whitham[1]基于不稳定性理论推导了一对非线性守恒型方程;Chu等人[2]修正了Whitham方程,并研究了波包在长时间范围内的演化。然而,边带不稳定性虽从非线性的角度较为成功地阐述了畸形波的生成机理,但对畸形波的波面函数、边带不稳定性的频率范围并未明确地给出,研究表明[3],基于弱非线性(小波陡ka<<1)和窄带谱假定(∣Δk∣/k<<1)的非线性薛定谔方程可较好地描述畸形波的波浪包络演化,畸形波的短暂性、大波高等特征与非线性薛定谔方程呼吸子解的特征符合良好。
1. NLS方程的数值计算方法
研究表明,对于形如式(1)的非线性薛定谔方程,存在如式(2)的孤波解
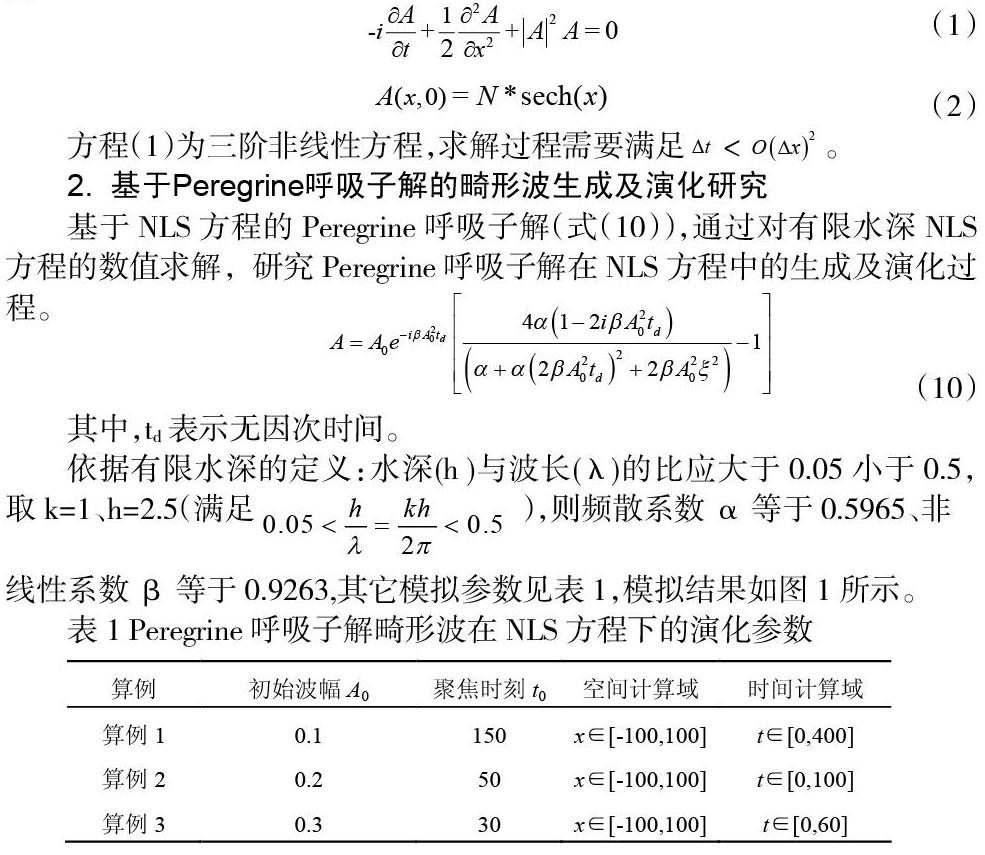
2. 基于Peregrine呼吸子解的畸形波生成及演化研究
基于NLS方程的Peregrine呼吸子解(式(10)),通過对有限水深NLS方程的数值求解,研究Peregrine呼吸子解在NLS方程中的生成及演化过程。
其中,td表示无因次时间。
线性系数β等于0.9263,其它模拟参数见表1,模拟结果如图1所示。
由图1可知:在算例1中,初始时刻(t=0),波浪几乎以正弦波的形式向前传播,仅在局部有微小扰动;畸形波生成时刻(t=150),波列最大波峰高度瞬间增大2倍(为载波波峰高度的3倍);片刻之后(t=175),最大波峰高度瞬间减小至最大波高的1/2;整个演化过程中,畸形波的生成和消失的时间为50(从t=125到t=175),远小于波浪的演化周期300,这说明了畸形波生成和消失的偶然性,且t=125时(畸形波生成前)和t=175时(畸形波生成后)存在较大的波峰和波谷,这说明畸形波生成前后会有较大的波峰和波谷生成。算例2至算例3呈现类似变化规律,这里不再赘述。
3. 小结
本文主要基于有限水深NLS方程,研究畸形波生成和演化规律,总结如下。
(1)基于一阶Peregrine呼吸子解畸形波解的分析。
(2)基于NLS方程的数值求解,研究一阶Peregrine呼吸子解畸形波在NLS方程中的生成和演化规律,研究表明:Peregrine呼吸子解畸形波发生时,常伴随较大的波峰和波谷,畸形波生成和消失具有偶然性。
参考文献:
[1]Whitham G B. Non-linear dispersion of water waves[J]. Journal of Fluid Mechanics, 2006, 27(2): 399-412.
[2]Chu V H, Mei C C. The nonlinear evolution of Stokes waves in deep water[J]. Journal of Fluid Mechanics, 1971, 47(4): 337-352.
[3]张晓. Matlab微分方程高效解法[M]. 北京, 机械工业出版社, 2016: 71.
作者简介:
罗春莲(1991-),女,汉族,福建龙岩人,教师,中共党员,助教,硕士研究生,主要从事畸形波及其对海洋结构物作用研究.
