武汉房价影响因素的实证分析
2019-10-21田思琪王新华
田思琪 王新华

武汉轻工大学
摘要:基于研究的1999-2017年数据建立相关的双对数回归方程模型,运用Stata软件进行分析数据结果。研究表明,武汉人口越多,武汉房价越高;武汉居民人均年消费水平越高,武汉的房价也会越高;武汉的建筑总产值越高,武汉房价越低。
关键词:武汉房价;影响因素;双对数回归模型
本文将基于收集整理的近十几年数据资料进行分析武汉房价的影响因素,在此建立计量经济學的相关模型,了解其主要因素和次要因素,并对所选的因素进行统计推断和经济意义上的检验,最后选择出拟合效果最好的因素得出结论并给予一些相关的政策建议。
一、文献综述及研究假设
作为国家的支柱产业,房价从根本上影响着国计民生,不仅只有武汉房价接连上涨,诸多地方的房价也被投资者炒得火热,与此同时,一些学者开始研究房价猛涨的背后原因。刘海云、吕龙(2018)研究了我国房价泡沫传染网络及其传染效应的影响因素,研究结果表明在房价泡沫猛增的过程中城市间房价泡沫传染效应发挥着重要作用,除此之外我国的经济发展状况、人口数量及其分布情况等因素也不能被忽略,对城市间房价泡沫传染效应有着显著的影响。
以上文献是基于我国整体房地产而言的,大部分研究方面都是宏观层次,而本文研究地区缩小为武汉,且主要在微观层次进行研究。本文选取的是面板数据,收集1999-2017年房价与以上研究的影响因素的数据,因此,本文提出如下四个假设:
H1:武汉地区的人口越多,武汉平均房价越高。随着人口的增加,居民对住房的需求量也会同步增加。
H2:武汉居民人均年消费水平越高,武汉平均房价越高。人均年消费水平越高,购买房屋的能力和投资欲望越强,房子更具有稳定性和保障性,越来越多的人看好这一投资机会,房价也因此被炒得越来越高。
H3: 武汉地区人均GDP越高,武汉平均房价越高。本文的人均GDP指标是在一年中平均每个人产生的价值,用来衡量经济发展状况,经济发展越快,也会带动房地产事业的发展。
H4:武汉建筑总产值越大,武汉平均房价越低。建筑业的总产值越大,意味着房子开发越多,开发投资的增加会对房价的上涨起到一定的抑制作用。
二、数据、变量、模型的选择
在数据选取方面,为减少多重共线性的影响,本文选取的是武汉近十几年(1999-2017)的平均房价以及人口数量、人均年消费水平、地区人均GDP和建筑总产值,来进行实证分析和研究检验。
在变量选取方面,本文将假设中提到的四个可能影响房价的因素都作为变量归结到模型中。
在模型选取方面,基于前文中提出的假设以及选取的变量,最后确定的模型为:
LnY=β0+β1LnX1+β2LnX2+β3LnX3+β4LnX4+u
在选取的模型中对因变量及自变量取对数处理,对数形式可以减少模型中的多重共线性,并能在一定程度上消除量纲和减弱异方差的影响,u是误差项,代表了未纳入模型中的变量的影响情况,还代表了在研究过程中的实验误差。
三、实证结果及分析
(一)参数估计
利用Stata软件进行回归估计,结果见表1。
表1 Stata回归结果分析
可得估计方程:
Lny=-36.3652+4.9083LnX1+1.0449LnX2-0.4450LnX3-0.3929LnX4
se= (10.3033(1.4360 ) (0.4006) (0.4032) (0.1462)
t= (-3.53) (3.42) (2.61) (1.10) (-2.69)
由表可知,该模型R2=0.9908,
(二)模型的计量检验
1、多重共线性的检验与修正
①计算方差膨胀因子VIF值检验多重共线性,计算结果见表2。
表2 LnX1-LnX4的VIF值
由结果知VIF=169.77,大于10,即表明存在高度多重共线性。
②对LnX1-LnX4在显著性水平ɑ=0.05进行检验,检验结果见表3。
表3 相关系数检验
在显著性水平为0.05的条件下在显著的t值后加“*”符号,强调对应变量之间高度相关,并且由以上的VIF结果可知LnX3对应的VIF的值较大为298.60,在下文的修正过程中应剔除X3。
③多重共线性的修正----逐步回归向前法
利用向前逐步回归法,得到修正后的回归结果如表4.
表4 逐步回归向前法修正后的回归结果
由回归结果知LnX1、LnX2和LnX4对应的p值均小于0.05,说明剔除掉X3后的模型回归结果显著。
④得出修正后的结果
Lny=-35.9044+4.9464LnX1+1.4168LnX2-0.3324LnX4
se=(10.3694)(1.4460) (0.2183) (0.1365)
t= (-3.46) (3.42) (6.49) (-2.43)
由表可知,修正后的模型R2=0.9900,
2、异方差检验及修正
①残差散点图检验
从输出结果可以推测出不存在扰动项,模型可能模拟得较为充分,怀疑不存在异方差,但是否存在異方差还需更精确的检验方法。
②怀特检验
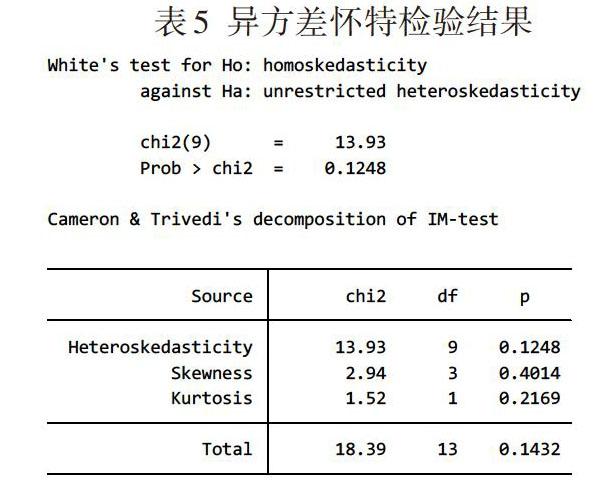
表5 异方差怀特检验结果
怀特检验结果显示,p值为0.1432,故在显著性水平为0,05的条件下接受原假设,说明不存在异方差,即不需要进行异方差的修正。
3、自相关检验及修正
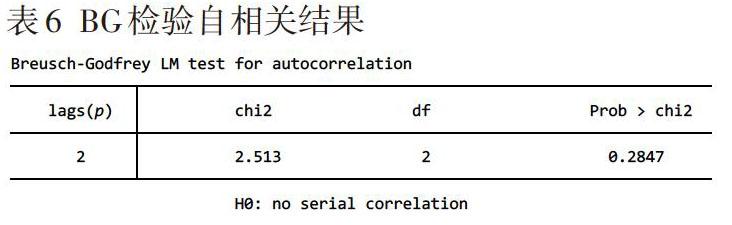
自相关检验——布鲁尔什-戈弗雷(BG)检验,结果见表6。
表6 BG检验自相关结果
从BG检验自相关结果可知,自相关假设检验对应的P值为0.2847,在显著性水平0.05的条件下不显著的,接受原假设H0,表明该模型中不存在自相关,不需要进行自相关的修正。
4、模型的确立
Lny=-35.9044+4.9464LnX1+1.4168LnX2-0.3324LnX4
se=(10.3694)(1.4460) (0.2183) (0.1365)
t= (-3.46) (3.42) (6.49) (-2.43)
由模型方程可知,自变量人口数量和人均年消费水平的系数均为正数,说明这两个变量均和应变量房价呈正相关,而自变量建筑总产值的系数为负数,说明此变量与房价呈负相关。
四、结论及政策建议
(一)结论
本文选取了人口数量、人均年消费水平、人均GDP以及建筑总产值这4个微观层次的影响因素,并使用Stata软件进行研究,在研究的过程中发现自变量人均GDP对房价不产生显著性的影响,故在修正过程中剔除这一自变量,最后的结果达到了实验的目的。
(二)政策建议
①有关部门应加强调控人口的流动情况,避免农村居民都移居至城市,否则会加剧城市住房的供应不足情况,导致房价的不稳定增长。
②制定明确的住房发展目标,加大保障性住房供给,合理安排住房供应商中商品房、政策性支持方及租赁住房比例,持续增加保障性住房比例。
③加大监督和执法的力度,严厉打击中介机构、房地产企业以及其他机构的违法行为,坚决抑制扰乱房地产市场的投机行为,一经查出则会严惩并进行曝光处理。
参考文献:
[1]黄厚霞、侯莉颖.房价影响综述 [J].天津出版总社,2011,(7):39-44.
[2]张世涵.房价对居民消费的影响及其区域差异研究[J].商业经济研究,2018(23):178-180.
[3]刘海云,吕龙.城市房价泡沫及其传染的“波纹”效应[J].中国工业经济,2018(12):42-59
作者简介:田思琪,女,武汉轻工大学经济与管理学院会计系大三学生,研究方向是会计。
王新华,男,武汉轻工大学经济与管理学院副教授,研究方向是计量经济学。
