基于神经网络的正弦波函数拟合实现研究

陈豪 吴健

摘  要：针对在人工智能教学当中，学生掌握线性回归之后对其他的初等函数的拟合实现产生的疑问，进行简单的教学研究。主要采用TensorFlow开源软件库，利用Python语言来编写神经网络程序。对于已有的呈现正弦波样态分布的点的集合进行训练，并通过调整训练参数最终得到拟合成功的正弦波模型，可以为其他的初等函数的拟合及以后基于训练模型的预测研究提供一些见解。

关键词：TensorFlow;Python;神经网络;正弦波;拟合

中图分类号：TP183;O174      文献标识码：A 文章编号：2096-4706（2019）21-0004-03

Abstract：We mainly focus on the questions of the fitting of other primary functions after students master linear regression in AI teaching，and then carries out some simple teaching research. It mainly uses TensorFlow open source software library and uses Python language to write neural network program. By training the existing set of points which present the distribution of sinusoidal wave patterns and adjusting the training parameters，the sinusoidal wave model can be successfully fitted，which can provide some insights for the fitting of other elementary functions and the prediction research based on the training model in the future.

Keywords：TensorFlow;Python;neural network;sine wave;fitting

0  引  言

在人工智能基础课程的教学中，对于线性回归的理解是掌握其他各种复杂的算法规律的第一步，紧接之后要学习的就是根据线性方程进行数据归类的预测。在各类基础的人工智能教学材料中，都将线性回归放在最前面予以讲授。在实际的教学过程中，因为学生对于線性方程在中学阶段已有掌握，对于线性回归的知识理解起来也并无大的障碍。但是掌握了线性回归之后，会自然而然地引向非线性的情况，应该如何进行回归计算并得出判断结论。提炼后，得到学生提出的具体问题是：在已知的初等函数中，除了线性方程外，是否其他的函数，如幂函数、对数函数、三角函数等的方程式皆可以成为回归的判断结论？本文就这个疑问，从初等函数中选取正弦波函数进行针对性的初步研究。

1  搭建环境与建立数据集

在人工智能的教学中主要采用主流的TensorFlow开源软件库，Google作为其开发者已经推广多年，各种开发环境与插件较为完善。如果采用国内百度的飞桨（PaddlePaddle）开源库同样可以完成此项任务，但主流教学中已经采用了TensorFlow，它的高使用率与高市占率可以让学生在对口企业中快速上手，有利就业，故采用TensorFlow开发。利用PyCharm IDE，配合安装Python 3.6版本，并导入TensorFlow的官方包，进行环境运行测试，成功后，指导学生开始开始建立训练所需的点数据集。这里还需要在PyCharm中安装pandas和NumPy工具插件，利用它们建立训练用数据集。

建立数据集分为三步，首先在[-π，π]之间生成400个平均分布的等距离点。关键语句为：

train_X = numpy.linspace（-math.pi， -math.pi， 400）

train_X = train_X.reshape（-1， 1）

train_X = train_X.astype（'float32'）

然后，为了让数据集看起来较为真实，需要添加微小扰动的干扰值，生成干扰值的关键语句为：

train_noise = numpy.random.normal（0， 0.03， train_X.shape）

train_noise = train_noise.astype（'float32'）

最后，完成训练点数据集的生成，关键语句为：

train_y = numpy.sin（train_X） + train_noise

这里使用利用Matplotlib库的pyplot对象显示训练集数据的分布状况，如图1所示。

2  建立神经网络与参数初始化

模拟正弦曲线涉及到非线性，这里利用神经网络来完成。TensorFlow中提供了方便地建立神经网络的搭建工具。对于正弦波拟合，搭建2层的神经网络就可以了。这里定义1个前置输入层、2个连接层、1个输出层的简单神经网络。2个连接层之间的连接的输出结果需要通过ReLU函数进行激活，然后数据进入第2个连接层，再次使用适当的权重与偏移，直接输出到输出层。整体神经网络的结构如图2所示。

3  模型训练

3.1  训练过程

模型的生成需要经过多次重复训练，最初设置循环2000次，但循环开始后，训练次数超过1000后图形基本无变化。经过反复测试得出，设置训练次数为800次既不耗费过多时间，也可以获得较好的训练效果。程序设置每经过40次训练循环，渲染当前图形并报告当前的损失函数。渲染当前图像采用plt的散点图，y值的显示范围设定-1.3到1.3，确保能够显示图形的全部部分，在进入到下一次40倍数的循环次数后，清空当前画面中已有的渲染点，将新的训练计算结果与x结对的点实时显示出来。

for step in range（800）：

session.run（optimizer.minimize（loss））

if step % 40 == 0：

predict = session.run（predict_y）

if step：

ax.lines.remove（lines[0]）

lines = ax.plot（X， predict， 'b-'， lw=5）

plt.title（'step： %d loss： %.4f' %（step， session.run（loss）））

3.2  结果拟合

经过多次循环运算之后形成了拟合样态效果。整体图形的变化趋势是，开始图形变换比较快，每经过40次循环后拟合弯曲形态和角度会有很大变化，但到了100次之后，变化幅度变小，图形只在细微的部分发生变化。观察损失函数的变化也具有这样的趋势。所以不进行平均取样展示，而是先前的取样间隔为40次，后期双倍次数取样。这里具体取样的是第0次、第40次、第80次、第120次以及第200次、第280次、第360次、第440次的拟合结果。损失函数也从最初的23.3060急速下降到了后期在0.0100以下，并缓慢变化到0.0040。抽取各次的图形后渐进的效果如图3所示。

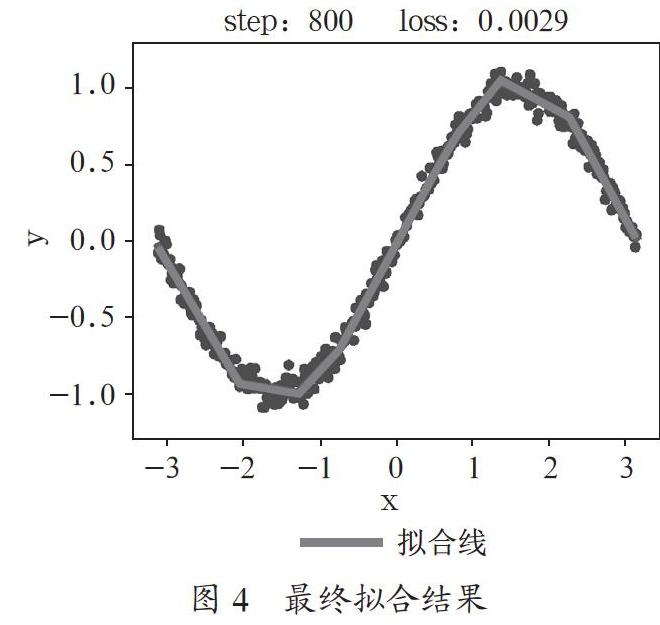
完成800次循环之后，最终拟合的图像如图4所示。损失函数降到0.0029。如果继续增加训练次数，损失函数无法继续下降，甚至會重新回到0.0030以上，所以本次训练的能够达到的损失函数最低为0.0029。

可以看到，其实在400次循环后，拟合效果已经较好。到800次结束时，红色拟合线已经基本与正弦曲线重叠，正弦函数模拟模型训练成功，可用于之后的预测。

4  结  论

通过以上的操作，利用神经网络，通过已有的训练数据集，实现了正弦波曲线的拟合。解答了学生的提出的疑问。还可以通过修改程序实现其他三角函数的拟态，以及其他初等函数，例如指数函数、对数函数，包括混合初等函数的拟合，学生可以利用之前学习到的高等数学知识进行举一反三的训练，增强对高等数学在人工智能中应用的理解。接下来，可以利用TensorFlow的模型保存与重载机制，进行新进数据的状态预测。总之，利用好TensorFlow或者PaddlePaddle开源工具，配合Python语言，将其融入到人工智能的教学中，以直观可视的方式让学生了解艰深的人工智能的知识。

参考文献：

[1] 刘帅奇，赵杰，刘明，等.新工科背景下基于教师科研成果转化的实践教学研究 [J].课程教育研究，2019（14）：39-40.

[2] 杨沛，谭琦，丁月华.一种面向非线性回归的迁移学习模型 [J].计算机科学，2009，36（8）：212-214+242.

[3] 周飞燕，金林鹏，董军.卷积神经网络研究综述 [J].计算机学报，2017，40（6）：1229-1251.

[4] 徐晓.计算机视觉中物体识别综述 [J].电脑与信息技术，2013，21（5）：4-6+41.

[5] 卢宏涛，张秦川.深度卷积神经网络在计算机视觉中的应用研究综述 [J].数据采集与处理，2016，31（1）：1-17.

作者简介：陈豪（1982-），男，汉族，江苏盐城人，讲师，硕士，主要研究方向：人工智能、大数据技术;吴健（1985-），男，汉族，江苏苏州人，实验师，硕士，主要研究方向：软件技术。