中央子午线对平面坐标转换精度的影响

曹学东 张新兵

摘要：本文介绍了四个具有代表性的平面坐标转换模型，并通过实例分析了相似变换模型和正形多项式模型的适用性，以及中央子午线对平面坐标转换精度的影响。对于区域性基础测绘和中小型工程测绘项目中涉及的平面坐标转换问题，具有一定的指导意义和实用价值。

关键词：中央子午线、相似变换模型、正形多项式模型、坐标转换、精度

众所周知，我国历史上采用的坐标系统包括1954年北京坐标系和1980西安坐标系以及众多的地方独立坐标系，并积累了大量的测绘成果。经国务院批准，我国自2008年7月1日起启用2000国家大地坐标系，新系统与现行国家大地坐标系转换、衔接的过渡期为8至10年。现有各类测绘成果在过渡期内可沿用现行国家大地坐标系并逐步转换到2000国家大地坐标系，2008年7月1日后新生产的各类测绘成果应采用2000国家大地坐标系[1]。对于区域性基础测绘和中小型工程测绘项目而言，坐标系统转换涉及两个方面，一是现有各类测绘成果的坐标系统逐步转换到2000国家大地坐标系，二是使用1954年北京坐标系或1980西安坐标系起算数据，生产2000国家大地坐标系测绘成果，而这些均涉及平面坐标的系统转换。由于高斯投影长度变形的特点，平面坐标的系统转换除要求重合点具有足够的数量、合理的分布和必要的精度外，新旧平面坐标的中央子午线和转换模型的选择也至关重要。

1 平面坐标转换模型

1.1 一般多项式模型

2.2 实例数据与解算结果

在北纬46°00′～46°16′、东经83°43′～83°59′区域（约1000km2），按2′的经纬间隔生成9×9个格网结点的大地坐标，以此作为1980西安坐标系的大地坐标，并据此在1980西安坐标系至2000国家大地坐标系的坐标改正数模型中内插得到相应的2000国家大地坐标系的大地坐标。对于格网结点的1980西安坐标系大地坐标，由东经81°00′～84°00′每隔30′作为一个中央子午线，分别计算相应的高斯投影平面坐标，共得到7个不同高斯投影带（平面坐标系）的平面坐标。2000国家大地坐标系的大地坐标则以东经84°作为中央子午线计算高斯投影平面坐标。

用7套不同中央子午线的高斯投影平面坐标分别解算转换为2000国家大地坐标系平面坐标的转换参数并统计其内部不符值情况，具体结果见表1。

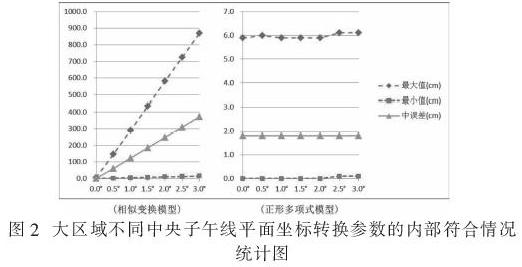
表1中Lo为源坐标即1980西安坐标系高斯投影平面坐标的中央子午线，dLo为源坐标中央子午线与目的坐标即2000国家大地坐标系高斯投影平面坐标中央子午线差值的绝对值。从中不难看出，相似变换模型的内部不符值与源坐标和目的坐标的中央子午线关系非常密切，其最大值、最小值和中误差均随着中央子午线差值的增大而增大，与中央子午线差值成正比。正形多项式模型的内部不符值则与源坐标和目的坐标的中央子午线没有关系，其最大值、最小值和中误差始终保持稳定且较小的水平。图1是将7套坐标转换参数的内部不符值情况以中央子午线差值为横轴、不符值数值为纵轴绘制成的折线图，亦更加直观地反映了这些变化规律。

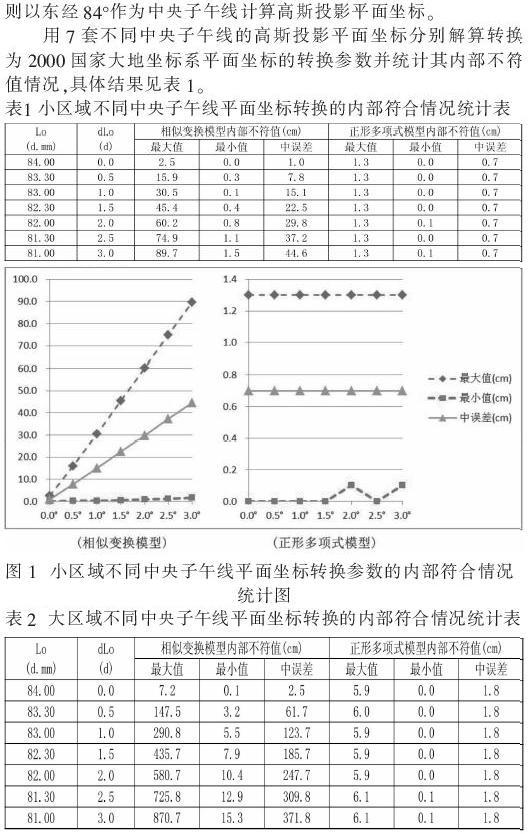
为了进一步证实上述变化规律，又在北纬46°00′～46°50′、东经83°09′～83°59′区域（约10000km2），按2′的经纬间隔生成26×26个格网结点的大地坐标，按相同的方法求得該区域不同中央子午线的高斯投影平面坐标分别解算转换为2000国家大地坐标系平面坐标的7套坐标转换参数的内部不符值（见表2、图2）。结果表明，其变化规律与前述完全一致。

3 结语

（1）相似变换模型适用于面积较小的转换区域，区域面积越小转换精度越高;区域面积相同的情况下，源坐标和目的坐标的中央子午线越接近转换精度越高，与中央子午线差值成正比。采用相似变换模型进行平面坐标转换时，应该将源坐标和目的坐标的中央子午线统一到相同的经线上，且转换区域面积不宜过大，具体的面积大小可以视内部不符值的情况而定。由于各类测绘地理信息商用软件均支持相似变换模型，所以其应用范围较大，在小区域基础测绘和小型工程测绘项目等方面都可以使用。

（2）正形多项式模型与转换区域面积、源坐标和目的坐标中央子午线的大小关系不大，即使在区域面积稍大、中央子午线相差较远的情况下也能够获得稳定且较高精度的转换结果。但是，各类测绘地理信息商用软件对其支持程度不高，所以正形多项式模型更适应于特定情况下的应用，如区域性基础测绘项目中的坐标转换或地、县（市）级基础测绘服务保障。

（3）一般多项式与正形多项式模型、仿射变换与相似变换模型的转换情况基本相同，本文限于篇幅关系没有列出。

（4）在实际坐标转换工作中，应该根据已有数据的情况进行预处理并选择适当的转换模型，然后依据转换结果的内部不符值中误差对重合点进行筛选，滤除大于2倍中误差的粗差点，以期转换结果达到技术要求的精度。

参考文献：

[1]国家测绘局.国家测绘局公告.2008（第2号）.

[2]黄维彬.近代平差理论及其应用[M].北京：解放军出版社，1992.

[3]曹学东.非线性坐标转换模型及其解算方法[J].创新与未来论文集，2004.

[4]OGP.Coordinate Conversions and Transformations including Formulas[J].Surveying and Positioning Guidance Note，2009.

（作者单位：新疆新力测绘工程有限公司）