水深及衬砌弹性模量对水工隧洞动位移的影响
2019-10-21胡良明孙奔博胡云鹤刘婷婷
胡良明 孙奔博 胡云鹤 刘婷婷

摘要:考虑水工隧洞在不同的输水深度和衬砌弹性模量条件下的地震动力响应变化规律,对研究水工隧洞在地震激励作用下的变形破坏机制非常重要。根据黏弹性人工边界和地下结构抗震计算理论,选取合理的材料参数和模型边界条件,应用ANSYS建立了某水工隧洞的三维有限元模型,对其施加拟合后的人工地震波,并采用瞬态分析法计算了隧洞结构模型在不同输水深度和衬砌弹模下的动位移变化规律。结果表明:输水深度在一定程度上可以改变水工隧洞抗震性能,水工隧洞随着输水深度的增加,水平位移和竖向位移受影响的程度有明显的区别,水平位移先增加后减少,竖直位移无明显规律;衬砌弹性模量能够在很大程度上影响水工隧洞的抗震性能,各参考点的水平位移随着衬砌弹性模量的增加呈现出先减小后增加,大部分参考点的竖直位移都在增加;水工隧洞在地震发生后其拱顶及拱肩受影响程度比较大,在水工隧洞设计中应特别关注。
关键词:水工隧洞;地震;输水深度;弹性模量:位移
中图分类号:TV312
文献标志码:A
doi:10.3969/j.issn.1000-1379.2019.03.023
人们普遍认为地下结构随着地基的运动而运动,故当地下结构在地震影响范围之内时,地下结构也会随着较弱的地面运动而发生相应的运动,不至于发生破坏。但是,这种毫无科学依据的观点被1995年发生在日本阪神的大地震证明是荒谬的,随着近年来越来越多的地下结构被发现在地震发生后受到不同程度破坏,人们不得不把研究的目光转向地下工程的抗震问题上来[1]。Kirzhner等[2]分析了隧道与围岩系统的地震反应,并总结了动力荷载对其稳定性的影响:Hashash等[3]提出了基于弹性壳体理论的盾构隧道地震响应拟静力分析方法:林皋等[4-8]归纳总结前人的研究成果,对地下结构与地面结构的震动特性进行了对比,得出了7个概括性结论:高峰等[5]比较了黏弹性边界、黏性边界和固定边界条件的精度,通过对地震荷载作用下隧道结构的反应分析,总结出了无限地基对计算结果的影响程度,以及地震作用下隧道衬砌容易破坏的位置。
水工隧洞作为水工建筑物不可缺少的组成部分,在水利工程建设中发挥着重要作用。与其他地下结构相比,水工隧洞不仅存在土与结构的相互作用,而且存在水与结构的相互作用,其地震反应比其他地下结构更复杂,因此研究输水深度及衬砌弹性模量对水工隧洞地震的影响不仅具有重要的工程价值,而且具有重要的理论意义。
1 地下结构抗震的基本原理
1.1 结构运动方程
结构通过有限元离散后,在运动状态下各节点的动力平衡方程如下:
2 有限元模型的建立
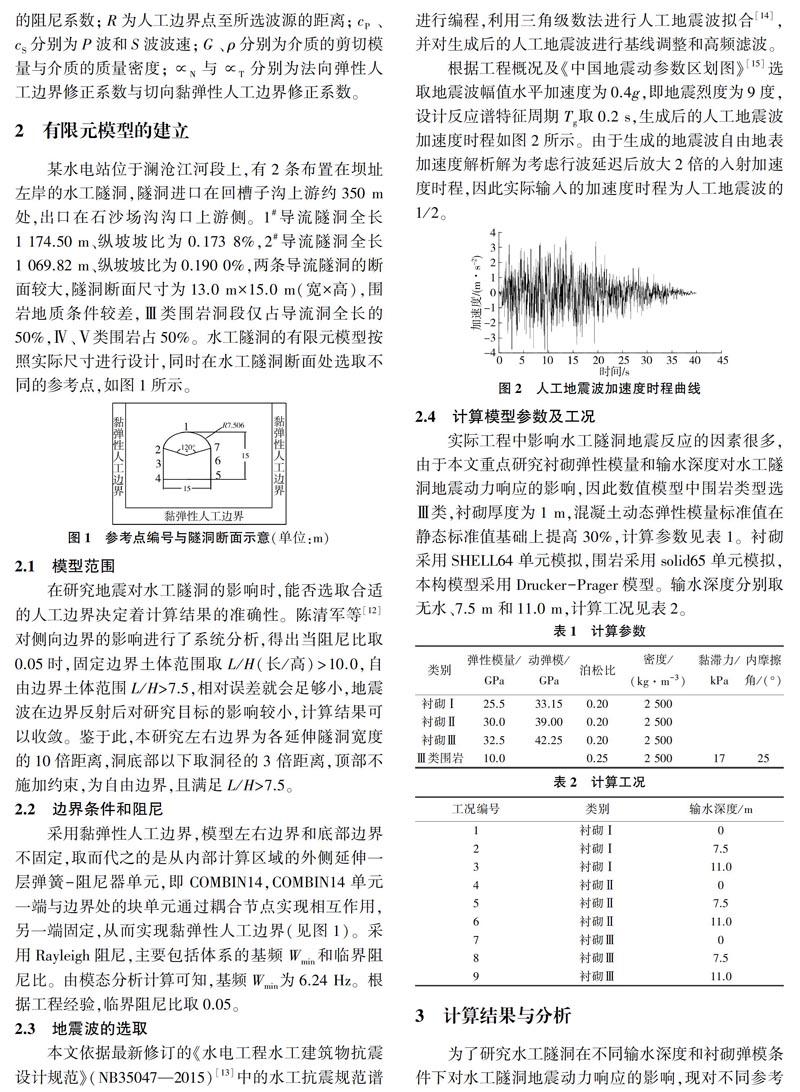
某水电站位于澜沧江河段上,有2条布置在坝址左岸的水工隧洞,隧洞进口在回槽子沟上游约350 m处,出口在石沙场沟沟口上游侧。1#导流隧洞全长1 174.50 m、纵坡坡比为0.173 8%,2#导流隧洞全长1 069.82 m、纵坡坡比为0.190 0%,两条导流隧洞的断面较大,隧洞断面尺寸为13.0 mx15.0 m(宽×高),围岩地质条件较差,Ⅲ类围岩洞段仅占导流洞全长的50%,Ⅳ、V类围岩占50%。水工隧洞的有限元模型按照实际尺寸进行设计,同时在水工隧洞断面处选取不同的参考点,如图1所示。
2.1 模型范围
在研究地震对水工隧洞的影响时,能否选取合适的人工边界决定着计算结果的准确性。陈清军等[12]对侧向边界的影响进行了系统分析,得出当阻尼比取0.05时,固定边界土体范围取L/H(长/高)>10.0,自由边界土体范围L/H>7.5.相对误差就会足够小,地震波在边界反射后对研究目标的影响较小,计算结果可以收敛。鉴于此,本研究左右边界为各延伸隧洞宽度的10倍距离,洞底部以下取洞径的3倍距离,顶部不施加约束,为自由边界,且满足L/H>7.5。
2.2 边界条件和阻尼
采用黏彈性人工边界.模型左右边界和底部边界不固定,取而代之的是从内部计算区域的外侧延伸一层弹簧一阻尼器单元,即COMBIN14,COMBIN14单元一端与边界处的块单元通过耦合节点实现相互作用,另一端固定,从而实现黏弹性人工边界(见图1)。采用Rayleigh阻尼,主要包括体系的基频W.。和临界阻尼比。由模态分析计算可知,基频Wmin为6.24 Hz。根据工程经验,临界阻尼比取0.05。
2.3 地震波的选取
本文依据最新修订的《水电工程水工建筑物抗震设计规范》( NB35047-2015)[13]中的水工抗震规范谱进行编程,利用三角级数法进行人工地震波拟合[14],并对生成后的人工地震波进行基线调整和高频滤波。
根据工程概况及《中国地震动参数区划图》[15]选取地震波幅值水平加速度为0.4g,即地震烈度为9度,设计反应谱特征周期T8取0.2 s.生成后的人工地震波加速度时程如图2所示。由于生成的地震波自由地表加速度解析解为考虑行波延迟后放大2倍的入射加速度时程,因此实际输入的加速度时程为人工地震波的1/2。
2.4 计算模型参数及工况
实际工程中影响水工隧洞地震反应的因素很多,由于本文重点研究衬砌弹性模量和输水深度对水工隧洞地震动力响应的影响,因此数值模型中围岩类型选Ⅲ类,衬砌厚度为1m.混凝土动态弹性模量标准值在静态标准值基础上提高300-/0,计算参数见表1。衬砌采用SHELL64单元模拟,围岩采用solid65单元模拟,本构模型采用Drucker-Prager模型。输水深度分别取无水、7.5 m和11.0 m,计算工况见表2。
3 计算结果与分析
为了研究水工隧洞在不同输水深度和衬砌弹模条件下对水工隧洞地震动力响应的影响,现对不同参考点的x(水平)方向位移、y(竖直)方向位移进行对比分析。
3.1 输水深度对水工隧洞动力响应的影响
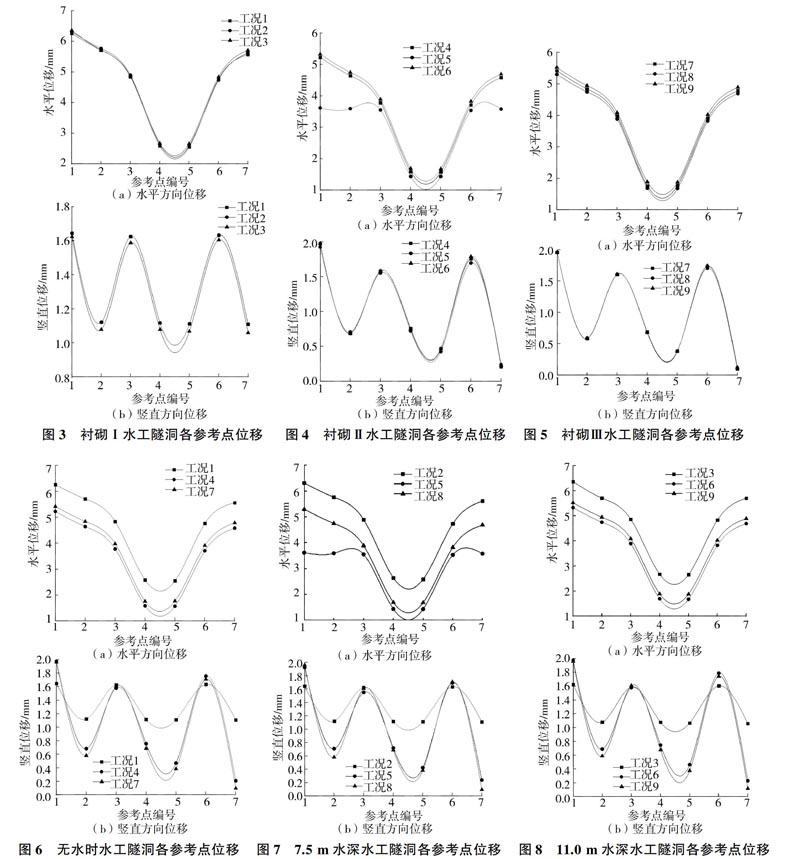
固定衬砌的弹性模量,对输水深度为0、7.5、11.0m情况下水工隧洞的位移进行分析。由图3-图5可以看出,随着输水深度的增大,水工隧洞各个参考点水平位移受地震激励的影响大体上在增大。水平位移在隧洞上部较大,在隧洞底部较小,基本上呈现出隧洞两侧左右对称的规律。竖直位移变化并没有呈现出规律性,随着输水深度的增大,各参考点竖直位移受影响程度不同,各参考点竖直位移变化幅度均低于5%。
3.2 衬砌弹性模量对水工隧洞位移的影响
为了研究水工隧洞在不同衬砌弹性模量下各参考点最大位移的变化规律,现对水工隧洞在地震激励中用下各参考点的最大位移(见图6-图8)进行分析。
由图6-图8可以看出:随着衬砌弹性模量的增大,隧洞水平位移基本上呈现先减小后增大的趋势;水工隧洞大部分参考点的竖直位移随着衬砌弹性模量的增大而减小:水工隧洞拱顶处的水平位移和竖直位移远大于其他部位的,拱肩处次之。
4 结论
(1)输水深度对水工隧洞的抗震稳定性有一定的影响,但水工隧洞并不会随着输水深度的增大而趋于更加不稳定的状态,相反,输水深度在一定程度上能够减轻水工隧洞受破坏的程度。
(2)衬砌弹性模量的改变对水工隧洞的抗震稳定性影响比较大。随着衬砌弹性模量的增大,水工隧洞的水平位移呈现先减少后增大的趋势,这说明结构抵抗外荷载的能力并不会随着弹性模量的增大而增强,相反,当结构越来越趋于刚性时,其本身更容易发生挤压或者断裂破坏。
(3)在不同输水深度或不同衬砌弹性模量条件下,水工隧洞各参考点水平位移的共同特征是在拱顶处比较大,在洞底处很小,隧洞中部水平位移处在顶部与底部的中间值:水工隧洞竖直位移的共同特征是在隧洞一侧的中部较大,在另一侧相对较小。
(4)在水利工程设计中合理地考虑输水深度和衬砌弹性模量,不仅能使水工隧洞抗震性能指标达到规范的要求,而且能达到降低工程造价的目的。对比不同工况下水工隧洞位移发现,当衬砌弹性模量接近20 GPa时,衬砌厚度更为安全经济,改变衬砌弹性模量不能改善其抗震性能,应采取其他更为有效的方法。
参考文献:
[1] 孙奔博,胡良明,付晓龙,围岩类型及衬砌厚度对水工隧洞地震动力响应的影响分析[J].水利水电技术,2017,48(3):12-18.
[2]KIRZHNERF,ROSENHOUSE G.Numerical Analysis of TunnelDynamic Response to Earth Motions[J].Tunneling andUnderground Space Technology ,2000, 15(3):249-258.
[3]HASHASH Y M A, HOOK J J,SCHMIDT B,et al.SeismicDesign and Analysis of Underground Structures[J].Tunneling and Underground Space Technology, 2001, 16(4):247-293.
[4]林皋,任红梅,复杂不均匀地层中地下结构波动响应频域分析[J].大连理工大学学报,2008,48(1):105-112.
[5] 陈健云,胡志强,林皋,大型地下結构三维地震响应特点研究[J].大连理工大学学报,2003,43(3):344-348.
[6]林皋,地下结构抗震分析综述(上)[J].世界地震工程,1990,6(2):1-11.
[7]林皋,地下结构抗震分析综述(下)[J].世界地震工程,1990,6(3):1-10.
[8]林皋,梁青槐,地下结构的抗震设计[J].土木工程学报,1996,29(1):15-25.
[9] 高峰,关宝树,隧道地震反应分析中几种边界条件的比较[J].甘肃科学学报,2004,16(1):110-112.
[10] 刘晶波,谷音,杜义欣,一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报,2006,28(9):1070-1075.
[11]谷音,刘晶波,杜义欣,三维一致粘弹性人工边界及等效粘弹性边界单元[J].工程力学,2007,24(12):31-37.
[12] 陈清军,杨永胜,土层随机地震反应分析中侧向边界的影响[J].岩土力学,2011,32( 11):3442-3447.
[13] 国家能源局,水电工程水工建筑物抗震设计规范:NB35047-2015[S].北京:中国电力出版社,2015:20-30.
[14] 谯雯,刘国明,肖振翔,等,水工建筑物设计反应谱人工地震波合成[J].水力发电学报,2013,32(5):232-238.
[15] 中国国家标准委员会,中国地震动参数区划图:CB18306-2015[S].北京:中国标准出版社,2015:10-15.
