济南市地表水控制指标动态管理研究

李锡铜　曹升乐　刘阳　刘超

摘要：“三条红线”是最严格水资源管理制度的核心，用水总量控制是“三条红线”之首。用水总量控制指标由地表水控制指标和地下水控制指标两部分组成。为研究地表水控制指标的动态管理方法，以国家分配的地表水用水总量控制指标为基础，建立不同频率年降水量与地表水控制指标的关系：利用马尔可夫过程理论，推断预报年的降水丰枯情况及年降水量，确定预报年的地表水控制指标：结合预报年年初地表水蓄水量，对预报年的地表水控制指标进行动态调整。以济南市为例，给出了地表水控制指标动态管理过程，最终确定济南市2017年地表水控制指标为2.39亿_3，原制定济南市2017年地表水控制指标为3.60亿_3，两者差异明显。

关键词：用水总量：控制指标：地表水;济南市

中图分类号：TV213.4

文献标志码：A

doi：10.3969/j.issn.1000- 1379.2019.03.016

水是生命之源，是人类生活和社会发展中无法替代的资源，也是生态系统中不可或缺的要素。随着我国人口的增长与社会经济的发展，对水资源的需求越来越大，水资源缺乏问题日益突出。为此，2011年中央一号文件明确提出实行最严格水资源管理制度，制定用水总量、用水效率和水功能区限制纳污“三条红线”[1]。用水总量控制是“三条红线”之首，用水总量控制指标的合理确定是水资源可持续利用、区域社会经济可持续发展的根本保障。

在取用水总量控制方面，国外部分学者对河流最大允许取水量进行了广泛研究，如D.L.Blanc等[2]预测了撒哈拉沙漠南部地区未来的缺水量：L- Collet等[3]通过构建水资源综合模型，评估了地中海地区中尺度流域的最大可供水量。“三条红线”具有鲜明的中国特色，陈军等[4]根据西双版纳地区的实际情况，构建了西双版纳“三条红线”控制指标体系：陈方等[5]基于用水总量控制红线，构建了太湖流域用水总量控制指标体系;刘淋淋等[6]通过对狭义、广义及严格意义地表（地下）水资源可利用量的对比分析，提出了用水总量控制指标的确定方法。目前，我国各流域水行政主管部门建立了比较完善的水资源管理体系。黄河流域水量调度及用水总量控制的工作开展较早，为用水控制指标的制定提供了许多可供借鉴的经验[7]。

目前，我国各地区未来一段时间的用水总量控制指标均按国务院办公厅2013年印发的《实行最严格水资源管理制度考核办法》规定再分配得到，为一固定值。笔者认为该控制指标（特别是地表水的控制指标）应随年降水量（地表水资源量）的丰枯而变化，同时受年初地表水蓄水量的影响。基于此，本文对地表水控制指标的确定方法进行研究。

1 地表水控制指标的确定方法

首先确定年降水量与地表水资源量的关系，根据分配的地表水控制指标，得到年降水量与地表水控制指标的关系：通过加权马尔可夫模型预测年降水量，确定地表水控制指标：最后结合年初蓄水量对控制指标进行调整。

1.1 年降水量与地表水控制指标的关系

地表水资源量的多少取决于年降水量的大小，而地表水的控制指标应以地表水资源量为基础。考虑到降水量年际差异，丰水年降水量大，对应的地表水资源量多，则地表水控制指标理论上应大一些：枯水年降水量小，对应的地表水资源量少，则地表水控制指标理论上应小一些。因此，首先分析年降水量与地表水动态控制指标的关系。

1.1.1 年降水量与地表水资源量关系确定

利用年降水量序列，用适线法确定年降水量频率曲线，进而确定不同频率的年降水量。据此建立年降水量与地表水资源量的关系方程，并推求不同频率年降水量对应的地表水资源量。

1.1.2 年降水量与地表水控制指标关系确定

年降水频率为50%即平水年时的降水量对应国家规定的地表水控制指标。年降水频率小于50%（即丰水情况）时，地表水控制指标原则上由地表水资源可利用量确定，以年降水频率5%（丰水年上限值）时对应的地表水资源量的40%为地表水控制指标的上限值：年降水频率为5% - 50%时，地表水控制指标呈线性变化，起点为地表水的控制指标，终点为地表水控制指标的上限值。年降水频率大于50%（即枯水情况）时，地表水控制指标原则上由地表水可供水量确定。分别确定年降水频率75%（偏枯年降水量）和95%（枯水年下限值）时的可供水量，即为年降水频率为75%和95%时对应的地表水控制指标。年降水频率为50% - 75%和75%- 95%时，地表水控制指标同样呈线性变化。因此，降水频率从95%到5%，年降水量与地表水控制指标的关系为3段分段函數。

1.2 年降水量预测

在制定用水控制指标时需要对当年的降水情况进行预测。年降水量序列可以通过多元线性回归[8]、灰色系统[9]、人工神经网络[10]、马尔可夫模型、模糊理论[11]等数值模拟方法来进行预测。相对于其他预测方法，马尔可夫模型是典型的定量预测方法，适用于中短期预测，且预测结果精度较好[12]，因此本文采用马尔可夫模型来预测年降水量的丰枯情况。

1.2.1 马尔可夫模型介绍

马尔可夫模型是一种以概率论和随机过程理论为基础，运用数学模型来分析客观对象发展变化过程的一种方法[13]。它最重要的特点是“无后效性”，要确定将来的状态，只需知道现在的状态即可。马尔可夫模型的统计特性完全由它的初始分布和转移概率确定[14]。对于离散型序列有：

1.2.2 马尔可夫模型预测年降水量的基本步骤

（1）区间的划分及丰枯状态确定。用均值标准差法将降水序列分为枯水、偏枯、平水、偏丰和丰水5个状态，分别对应空间状态1、2、3、4、5。

（2）转移矩阵的确定。按上述分级标准确定降水序列中各年降水量所对应的状态，利用式（1）和式（2）对所得的结果进行统计计算，可得不同步长马尔可夫模型的转移概率矩阵。

（3）计算年降水序列的各阶自相关系数“及各步长的权重w_k。

自相关系数r_k计算公式为

1.2.3 均值标准差法

水文序列的丰枯区间划分有很多种方法，如要素距平值法、均值标准差法、保证率法、集对分析法等。结合各方法优缺点、适用性及研究区实际情况，本文采用均值标准差法。

均值标准差法同时考虑了均值和方差的影响，其通用划分标准为x+bs（x为水文序列均值、s为水文序列标准差、b为系数）。

运用均值标准差法将丰枯状态按照枯水、偏枯、平水、偏丰、丰水5级划分，常见划分标准见表1。

1.3 地表水控制指标的动态调整

根据预测的年降水量确定当年地表水控制指标后，需对该指标进行调整。地表水用水指标的确定不仅要考虑年降水量的影响，而且应反映年初蓄水量的多少，地表水蓄水量用水库与湖泊的蓄水量来表示。

分析年初地表水蓄水量长序列资料，确定年初地表水合理的蓄水量值（可采用地表水年初蓄水量的多年平均值）。当年初的地表水蓄水量小于合理的蓄水量时，应适当减小当年地表水指标：当年初的地表水蓄水量大于合理的蓄水量时，可适当增加当年地表水指标。减小（或增大）的具体值应以年初地表水蓄水量对应的可利用量为基础综合确定，同时考虑蒸发和渗漏的影响。

依据预测得到的年降水量推求地表水控制指标，并结合年初蓄水量对控制指标进行调整的方法称为地表水控制指标的动态管理方法。

2 应用实例

以山东省济南市为例，对2017年地表水控制指标进行动态管理研究。济南市水资源主要来自大气降水和过境河流，由当地地表水、地下水和客水组成。济南市水资源具有总量不足、年际变化大、年内分配不均和地域分布不均等特点。济南市为资源性缺水地区，是全国重点缺水城市之一。济南市多年平均降水量为645.6 mm，多年平均水资源量为15.70亿m³，其中地表水资源量为7.94亿m³。由山东省用水总量控制指标确定的济南市2017年地表水的控制指标为3. 60亿m³。

2.1 济南市年降水量与地表水控制指标的关系

2.1.1 济南市年降水量与地表水资源量的关系

济南市2000-2016年年降水量与地表水资源量的关系见图1，用各种线形进行分析、拟合，结果表明一次函数的拟合度最高。推求出的年降水量与地表水资源量的回归方程为

y= 0.028 5x - 10.622 （R²= 0.936 8）

（6）

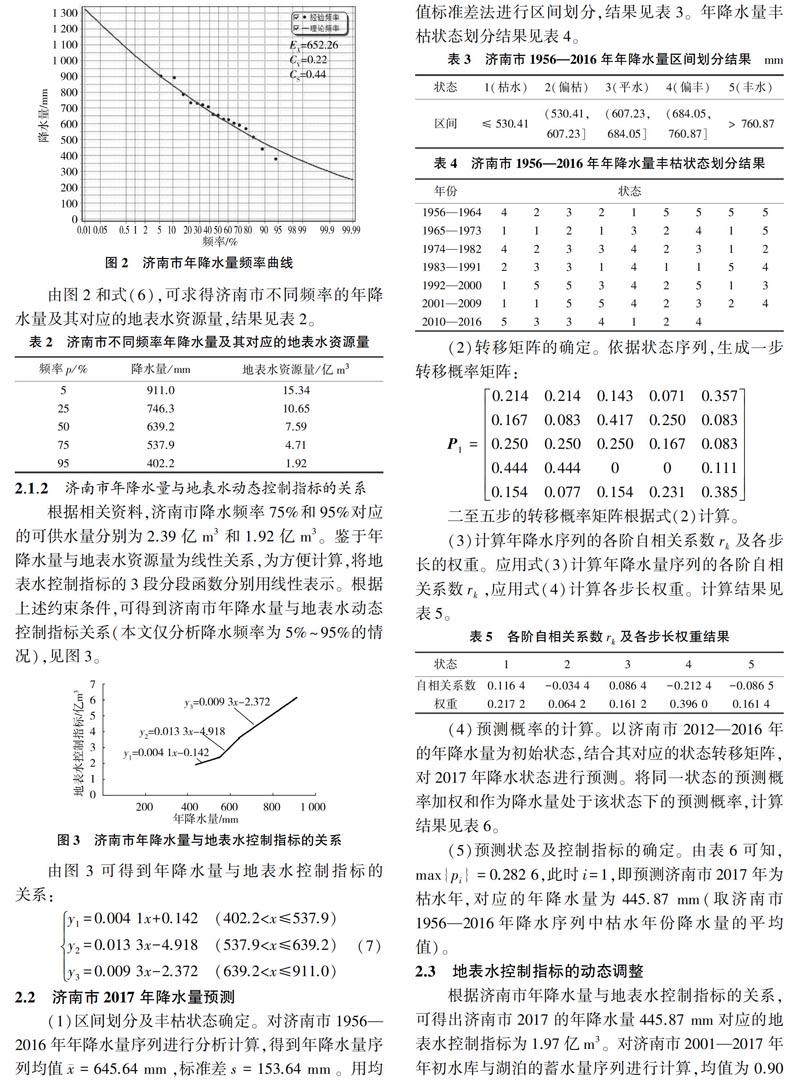
利用济南市1956-2016年降水量序列，确定降水量频率曲线，适线结果见图2。

由图2和式（6），可求得济南市不同频率的年降水量及其对应的地表水资源量，结果见表2。

2.1.2 济南市年降水量与地表水动态控制指标的关系

根据相关资料，济南市降水频率75%和95%对应的可供水量分别为2.39亿m³和1.92亿m³。鉴于年降水量与地表水资源量为线性关系，为方便计算，将地表水控制指标的3段分段函数分别用线性表示。根据上述约束条件，可得到济南市年降水量与地表水动态控制指标关系（本文仅分析降水频率为5% - 95%的情况），见图3。

由图3可得到年降水量与地表水控制指标的关系：

Yi= 0.004 lx+0.142 （402.2

y2= 0.013 3x-4.918 （537.9

y3= 0.009 3x-2.372 （639.2

2.2 济南市2017年降水量预测

（1）区间划分及丰枯状态确定。对济南市1956-2016年年降水量序列进行分析计算，得到年降水量序列均值x= 645.64 mm，标准差s=153.64 mm。用均值标准差法进行区间划分，结果见表3。年降水量丰枯状态划分结果见表4。

（2）转移矩阵的确定。依据状态序列，生成一步转移概率矩阵：

二至五步的转移概率矩阵根据式（2）计算。

（3）计算年降水序列的各阶自相关系数r_k及各步长的权重。应用式（3）计算年降水量序列的各阶自相关系数r_k，应用式（4）计算各步长权重。计算结果见表5。

（4）预测概率的计算。以济南市2012-2016年的年降水量为初始状态，结合其对应的状态转移矩阵，对2017年降水狀态进行预测。将同一状态的预测概率加权和作为降水量处于该状态下的预测概率，计算结果见表6。

（5）预测状态及控制指标的确定。由表6可知，max{pi}=0.282 6，此时i=l，即预测济南市2017年为枯水年，对应的年降水量为445. 87 mm（取济南市1956-2016年降水序列中枯水年份降水量的平均值）。

2.3 地表水控制指标的动态调整

根据济南市年降水量与地表水控制指标的关系，可得出济南市2017的年降水量445.87 mm对应的地表水控制指标为1.97亿m3。对济南市2001-2017年年初水库与湖泊的蓄水量序列进行计算，均值为0.90亿m³：济南市2017年年初水库与湖泊的蓄水量为1.42亿m³（考虑蒸发与渗漏的影响，系数为0.8），地表水控制指标可增加0.42亿m³。因此，最终确定济南市2017年地表水控制指标为2.39亿m³，与根据山东省用水总量控制指标确定的济南市2017年地表水控制指标为3.60亿m³相比少了1.21亿m³，说明年降水量以及年初水库与湖泊的蓄水量对地表水控制指标的影响较大，地表水控制指标的动态管理研究有实际意义。

3 结语

（1）以国家分配的地表水用水总量控制指标为基础，通过研究预报年的降水年型和地表水年初蓄水量对地表水控制指标的影响，提出了地表水控制指标的动态管理方法。并以济南市为例，对其2017年地表水资源量的控制指标提出了具体调整方案。通过调整后的地表水控制指标与原分配指标进行对比可以看出，两者差异明显，说明地表水控制指标的动态管理研究有实际意义。

（2）地表水控制指标的动态管理方法适用于我国北方大部分地区，对于充分利用地表水资源、保障地区社会经济的可持续发展具有十分重要的现实意义，对其他地区地表水总量控制指标的制定具有借鉴意义。

（3）地表水控制指标的确定受多种因素的影响，目前这方面的研究成果不多。本文仅考虑了预报年的降水年型和年初地表水蓄水量，下一步需要对该方法进行深入研究。

参考文献：

[1]王浩，实行最严格水资源管理制度关键技术支撑探析[J].中国水利，2011（6）：28-29.

[2]BLANC D L，PEREZ R.The Relationship Between Rainfalland Human Density and Its Implications for Future WaterStress in Sub-Saharan Africa[J].Ecological Economics，2008，66（2）：319-336.

[3]Collet L，Ruelland D， Borrellestupina V， et al.IntegratedModelling to Assess Long-Term Water Supply Capacity of aMeso-Scale Mediterranean Catchment[J]. Science of theTotal Environment， 2013， 461-462（7）：528-540.

[4] 陳军，杨国胜，武晓文，等，西双版纳最严格水资源管理“三条红线”控制指标体系研究[J].水电与新能源，2014（3）：6—9.

[5]陈方，盛东，高怡，等，太湖流域用水总量控制体系研究[J].水资源保护，2009，25（3）：37-40.

[6]刘淋淋，曹升乐，于翠松，等，用水总量控制指标的确定方法[J].南水北调与水利科技，2013，11（5）：159-163.

[7]孔祥磊，黄河山东段河道治理与工程质量控制研究[D].济南：山东大学，2012：27-47.

[8]张晓伟，黄领梅，沈冰，等，灰色自记忆神经网络模型在年径流预测中的应用[J].西安建筑科技大学学报（自然科学版），2006，38（6）：761-764.

[9]邓聚龙，灰色系统基本方法[M].武汉：华中理工大学出版社，1987：74-89.

[10]张青贵，人工神经网络导论[M].北京：中国水利水电出版社，2004：67-81.

[11]杨纶标，高英仪，凌卫新，模糊数学原理及应用[M].5版，广州：华南理工大学出版社，2011：52-76.

[12] 冯朝山，基于加权马尔可夫模型的降水预测研究[J].人民黄河，2009，31（4）：31-33.

[13]冯虹，邹华，魏文元，马尔可夫链在教学质量评价中的应用[J].天津师范大学学报（自然科学版），1999，l9（1）：6-10.

[14]朱宁，李竹梅，马尔可夫过程在教学管理中的应用[J].桂林电子工业学院学报，2000，20（2）：74-77.