基于PID及前馈-反馈的换热器控制系统

张璐

摘 要：现阶段，换热器的温度控制不仅存在很大的滞后性，而且还存在很多扰动因素。通常PID控制在过程控制中总能取得较好的控制效果，但当扰动因素较多时，仅使用PID控制方法往往效果不佳。故本文以不考虑扰动因素的PID控制为基础，分析了构成存在扰动因素时的前馈-反馈系统。该系统不仅有效消除了温度控制存在的纯滞后问题，而且使扰动因素对系统稳定性的影响降到最小，得到较好的控制性能。

关键词：纯滞后;扰动;PID;前馈-反馈

中图分类号：TQ051.5文献标识码：A文章编号：1003-5168（2019）16-0085-03

Abstract： The temperature control of heat exchanger not only has great lag， but also has many disturbance factors. Usually， PID control can always achieve better control effect in process control， but when there are many disturbance factors， only using PID control method is often not good. Therefore， based on the PID control without considering the disturbance factors， the feedforward feedback system with disturbance factors is constructed in this paper. Not only the pure lag problem of temperature control is effectively eliminated， but also the influence of disturbance factors on the stability of the system is minimized， and the better control performance is obtained.

Keywords： pure lag;perturbed;PID;feedforward-feedback

换热器又叫做热交换器，是化工、石油、动力、食品及其他许多工业部门的通用设备，在生产中占有重要地位。

1 系统数学模型

1.1 换热器的特性

图1为换热器的基本换热原理，其中[G1]、[G2]分别为工艺介质及载热体的流量;[T1i]、[T2i]分别为工艺介质及载流体的入口温度;[T1o]、[T2o]分别为及载流体的出口温度;[c1]、[c2]分别为工艺介质及载热体的比热容。

热量平衡方程为[1]：

（1）

式中，[q]为传热速率（单位时间内传递的热量）;[G]为质量流量;[c]为比热容;[T]为温度。

传热过程中的传热速率为：

（2）

式中，[K]为传热系数;[F]为传热面积;[ΔT]为两流体间的平均温差。

其中，平均温差[ΔT]对于逆流、单程的情况为对数平均值表示如下：

（3）

当[13≤T1i-T1oT2o-T2i≤3]时，误差在5%以内，可采用算术平均值来代替，算术平均值表示为：

（4）

整理可得热换器的静态特性方程为：

（5）

流体出口温度为：

（6）

1.2 换热器的动态特性

换热器由于两侧都不发生相变，动态特性为分布参数的非线性方程，但为了说明换热器动态特性的基本规律，可以用近似关系来描述。

①由于出口温度增量与工艺介质入口温度增量是线性关系，故工艺介质入口温度[T1i]对出口温度[T1o]的影响可用以纯滞后环节来描述，即

（7）

②同理，由于出口温度增量与载热体流量增量成线性关系;而与载热体流量的增量、工艺介质流量的增量成非线性关系。故入口温度[T2i]、流量[G2]及工艺介质流量[G1]对出口温度[T1o]的影响可用带有纯滞后的二阶惯性环节来近似，即：

（8）

2 被控对象及性能分析

2.1 被控对象

由上述分析，可假设载热体的被控对象动态特性为：

（9）

即

（10）

当影响出口温度的其他3个变量变化较频繁、幅值波动较大时，工艺介质流量波动大且变量可测量，可构成工艺介质为前馈信号和载热体流量的前馈-反馈控制系统，设干扰通道的传递函数为：

（11）

2.2 被控对象性能分析

由MATLAB得到被控对象闭环系统的阶跃响应曲线，如图2所示。该系统带有滞后性，不是一有输入就有输出结果，而是经过了很长时间的滞后才有响应。而且，该系统最大超调量过大，所以在减小滞后时间的同时，还要减小最大超调量。

3 热换器的控制方案

3.1 单回路控制系统

图3是控制系统方框图，其中，[Gcs]为需要设计的控制器，希望在该控制器的控制调节作用下，使系统获得较好的性能。

3.2 前馈-反馈控制系统

前馈控制补偿器的传递函数应为：

（12）

該载热体前馈-反馈控制系统方框图如图4所示。

由于扰动是由除载热体流量以外，工艺介质入口温度、工艺介质流量、载热体入口温度这3个变量造成的，故该扰动是一个带有纯滞后的二阶环节。可知，其传递函数模型为：

（13）

可假设其中的增益、时间常数及滞后：

（14）

设前馈控制补偿器的近似传递函数的形式为：

（15）

[Td1]、[Td2]为动态前馈时间常数，可在Simulink仿真中对其进行整定。

4 基于PID的控制器设计

4.1 单回路控制系统的PID控制器设计

PID控制系统[3]由PID控制器和被控对象组成。[et]为控制器的输入量，将[et]的比例[P]、积分[P]和微分[D]通过线性组合构成控制量，对被控对象进行控制，其控制规律为：

（16）

其传递函数形式：

（17）

式中：[KP]表示比例系数;[TI]表示积分时间常数;[TD]微分时间常数;[KP]、[TI]、[TD]选取决定控制器的性能。

利用试凑法调节PID参数，依次调节P、I、D的大小，经反复试凑得到最佳阶跃响应图，如图5所示。

其中，得到PID的3个参数为[KP]=0.25，故取[Ki]=0.007，[KD]=2.5。于是，得到PID控制器：

4.2 整定前控制器參数

设前馈控制器的模型为：

（19）

现讨论控制器参数[Kf]以及[T1]和[T2]的工程整定[4]。

4.2.1 整定静态前馈系数。当系统无前馈时，设系统在输入[x0]、扰动[m0]作用下，系统输出为[y0]，然后接入前馈回路，调节前馈控制器的静态系数[Kf]，使系统稳定时输出恢复[y0]，此时的[Kf]值即为所求得的前馈控制器的静态系数。

令[Kf]=0，[T1]=0，[T2]=0，输入[x0]=5，干扰为[m0]=0，得系统的响应曲线，如图6中的实线。加入阶跃扰动后，系统响应曲线如图6所示。

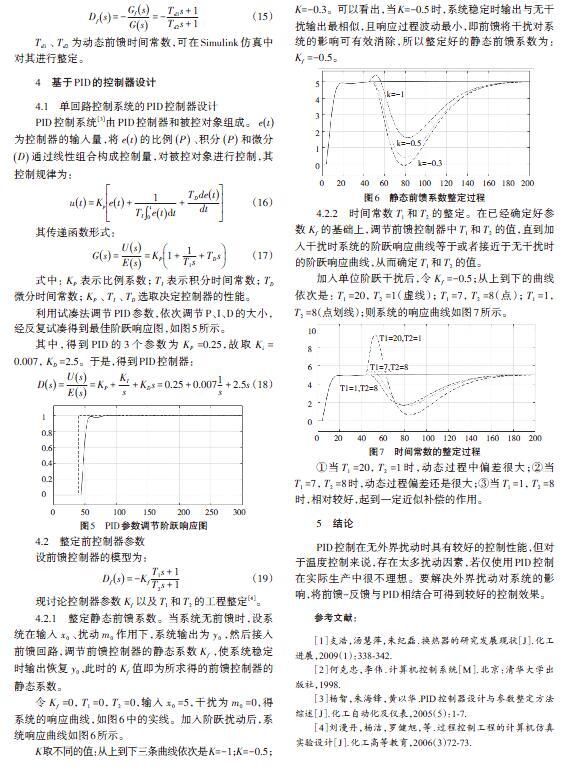
K取不同的值：从上到下三条曲线依次是K=-1;K=-0.5;K=-0.3。可以看出，当K=-0.5时，系统稳定时输出与无干扰输出最相似，且响应过程波动最小，即前馈将干扰对系统的影响可有效消除，所以整定好的静态前馈系数为：[Kf]=-0.5。

4.2.2 时间常数[T1]和[T2]的整定。在已经确定好参数[Kf]的基础上，调节前馈控制器中[T1]和[T2]的值，直到加入干扰时系统的阶跃响应曲线等于或者接近于无干扰时的阶跃响应曲线，从而确定[T1]和[T2]的值。

加入单位阶跃干扰后，令[Kf]=-0.5;从上到下的曲线依次是：[T1]=20，[T2]=1（虚线）;[T1]=7，[T2]=8（点）;[T1]=1，[T2]=8（点划线）;则系统的响应曲线如图7所示。

①当[T1]=20，[T2]=1时，动态过程中偏差很大;②当[T1]=7，[T2]=8时，动态过程偏差还是很大;③当[T1]=1，[T2]=8时，相对较好，起到一定近似补偿的作用。

5 结论

PID控制在无外界扰动时具有较好的控制性能，但对于温度控制来说，存在太多扰动因素，若仅使用PID控制在实际生产中很不理想。要解决外界扰动对系统的影响，将前馈-反馈与PID相结合可得到较好的控制效果。

参考文献：

[1]支浩，汤慧萍，朱纪磊.换热器的研究发展现状[J].化工进展，2009（1）：338-342.

[2]何克忠，李伟.计算机控制系统[M].北京：清华大学出版社，1998.

[3]杨智，朱海锋，黄以华.PID控制器设计与参数整定方法综述[J].化工自动化及仪表，2005（5）：1-7.

[4]刘漫丹，杨洁，罗健旭，等.过程控制工程的计算机仿真实验设计[J].化工高等教育，2006（3）72-73.