简述飞行模拟器比力矢量运算
2019-10-21康峰
康峰

摘 要 在全动飞行模拟器运动系统中,对加速度的仿真是个非常重要的指标,飞行员在驾驶舱内,不仅能感受到车辆的加速度,同时还能感受到重力的加速度。三轴比力矢量的计算是建立运动系统加速度最基本的一步。
关键词 比力矢量;加速度;轴系统
引言
随着中国民航事业和中国大飞机制造业快速的发展,飞行模拟器的需求也越来越大。而我国的自主生产全动飞行模拟器发展却非常缓慢,瓶颈就在于运动系统的仿真和其工作的稳定性。随着现代技术不断提高,世界各先进的模拟机生产厂如CEA;L3等的飞行模拟器运动系统,其成本越来越低,性能越来越好。本文就将对其运动系统中最关键的指标:加速度做出研究。
1轴系统的建立
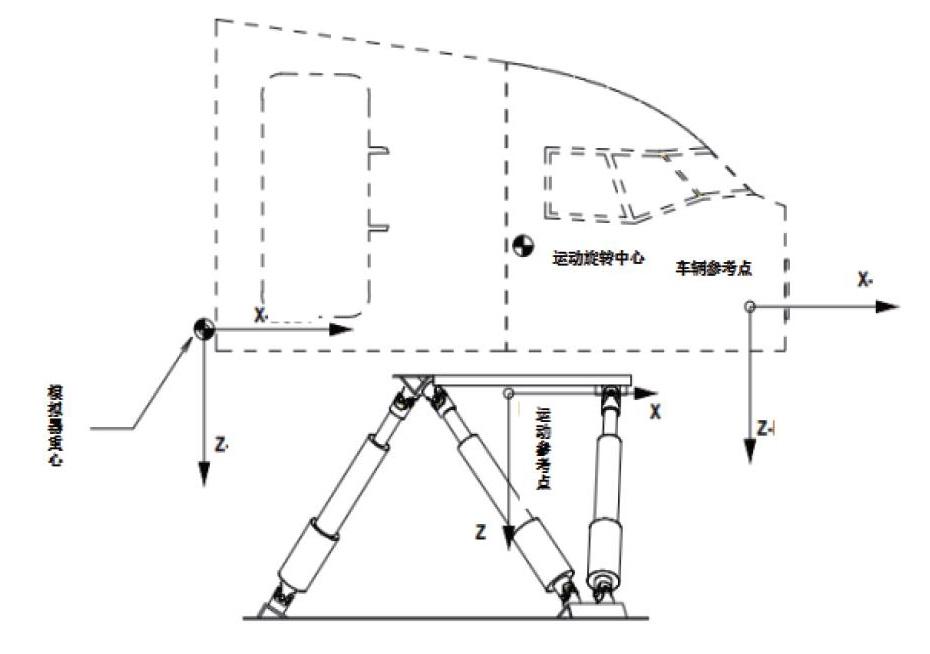
为了描述模拟器位置和姿态必须选择一些坐标系作为参考基准,下图显示了飞行模拟器运动系统应用中不同参考点和轴系统的位置,使用以下参考点和轴系统:
(1)运动参考点:运动平台坐标系固定在运动平台上。运动平台坐标系的XY平面位于顶部连接平面内。Z轴向下。运动平台坐标系的原点位于顶部旋转接点所组成的三角形的质心,这是运动系统上关节三角形的原点称为运动参考点。
(2)运动旋转中心:这是驾驶员的位置。运动软件将指令的线性和旋转加速度转换到这一点。
(3)车辆参考点:这里之所以定义为车辆,是因为驾驶舱中的飞行员能感觉到车辆的线速度。车辆参考点是车辆参考系统的原点。这里飞行模拟器的重心、运动旋转中心、运动参考点都在本车辆参考系统中定义[1]。
(4)模拟器座舱重心:这是实际模拟器重力中心。重心的位置在车辆参考系统中确定,并由主计算机发送。重心也是模拟器轴线系统的原点。线性加速度和旋转加速度是沿着和关于模拟器轴给出的。
惯性轴系统固定在地上。惯性轴系统中的偏移是根据处于中立位置的运动参考点的位置来测量的。
以上就是模拟器轴系统的建立,所有坐标系都是右手坐标系。正X向指向行驶方向,正Y向指向右侧,正Z向指向下方 。
2比力及其比力矢量计算
在三维空间中,描述一个刚体运动要六轴,三轴加速度,三轴角速度。用加速度传感器可以测量加速度的值,是测量轴向的力。
比力,就是单位质量上作用的非引力外力,通常我们用加速度计测量的不是载体的运动加速度,而是载体相对于惯性空间的绝对加速度和引力加速度之差,这就是比力。在飞行模拟器应用中,直线加速度通常由主机以比力的形式传输。驾驶舱中的飞行员不仅能感觉到如同车辆的线性加速度,还能感觉到重力加速度[2]。
通常情况下飞行员所感觉到的是加速度和重力加速度之间的矢量差,这和加速度计测量的一样。当假定飞行员的质量为m时,作用于飞行员的力为m×a(由于车辆加速)和m×g(由于重力),作用于飞行员的总力矢量是m×(a-g)。这就是比力,定义为单位质量上所有力的总和。
2.1 比力矢量
这里必须沿着车轴系统解析比力矢量,以获得比力Axb、Ayb和Azb(車身轴系统的原点位于车辆重心)。在一般线性加速度计测量是比力(a+g)不能分辨出重力加速度g和运动加速度a,一个加速度计只能测量一个方向的比力,测量矢量必须使用三个加速度计,三个加速度计垂直安装可测量比力矢量,进而得到运动加速度。假设沿着车身轴的三个轴安装三个线性加速度计系统。每个加速度计测量线性加速度和重力分量(比力)之差。这里大写字母A代表比力以区分线加速度,b(body)代表驾驶员身体,用xb、yb、zb表示沿着车身轴线系统驾驶员x y z方向,使车辆线速度为(vxb、vyb、vzb)加速度计的输出为[3]:
2.2 加速度传感器测量倾角原理
三轴加速度以重力为输出矢量来决定物体在空间的姿态,把加速度传感器国定在物体水平面上,当物体姿态改变时,通过测量由于重力引起的加速度,可以计算出设备相对于水平的倾斜角度,通过分析动态的加速度,可以分析出设备的移动的方式。使作用在车身上的重力为(Fxbg,Fybg,Fzbg),当车身轴线系统相对于地球固定轴线系统的姿态表示为欧拉角φ(关于x轴)和θ(关于y轴),然后车身轴系统中的重力分量为:
3结束语
以上便是关于比力矢量的数学解析,比力Axb、Ayb和Azb是运动计算机(变量AX AY和AZ)的输入,通过计算机洗出算法对飞机起飞过程中的水平加速和角速度信号进行洗出滤波,得到运动平台的加速度和角速度指令信号,来控制模拟器的运动作动筒运动,从而使驾驶员不仅能感受到车辆的加速度同时还能感受到重力的加速度,这一指标在模拟器模拟飞机起飞形态时最为重要[4]。
参考文献
[1] 王辉,朱道杨,平凡.基于模糊逻辑的高逼真度运动体感算法研究[J].系统仿真学报,2017,(3):546-551.
[2] 董新民,王小平.飞行模拟器电动式纵向操纵人感系统的研究[C].中国航空学会第八次飞行器控制与操纵学术交流会.中国航空学会第八次飞行器控制与操纵学术交流会论文集.湖北襄樊:中国航空学会,1999:92-96.
[3] 吴重光.仿真技术[M].北京:化学工业出版社,2000:179.
[4] 王行仁.飞行实时仿真系统技术[M].北京:北京航天航空大学出版社,1998:31.
