中考里的“有理数”

文 季红娟

有理数是每年各地中考必考的基础知识，涉及的题型和知识点还是比较多的。此外，对于本章中最基本的分类讨论、数形结合等数学思想，也是同学们后续学习要掌握的。下面，我们将近两年各地中考中有关有理数的考点进行归纳、解析，以帮助同学们更好地掌握相关内容。

考点1 相反数、绝对值、倒数的定义

此类问题考查的都是相反数、绝对值、倒数的相关概念。熟知并能熟练运用定义最关键。在此基础上，结合数轴渗透数形结合思想，结合绝对值渗透分类讨论思想，对概念的运用便能进一步深化。

例1（2018·绥化）的相反数是（）。

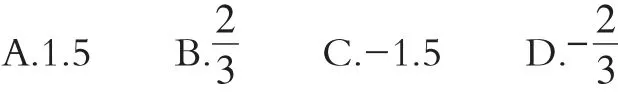
【解析】根据相反数的定义解答。选A。

【点评】此类题目是最基础的有理数定义类型的题。理清相关概念是关键。

变式1（2017·包头）a2=1，b是2的相反数，则a+b的值为________。

A.-3 B.-1 C.-1或-3 D.1或-3

【解析】本题结合了有理数的乘方、相反数和有理数的运算，是中考中对计算能力最基本的要求。考虑到有平方，分类讨论：①当a=-1，b=-2时，a+b=-3；②当a=1，b=-2时，a+b=-1。故选C。

考点2 实际问题中的有理数运算

有理数的混合运算是初中数学中最基本的运算，熟悉并能熟练运用有理数的运算法则是关键。如果将有理数的运算赋予实际问题的背景，我们便需要从实际问题中提炼出数学模型，理解这是数学中的哪类问题，并能熟练解决。

例2（2018·咸宁）咸宁冬季里某一天的气温为-3℃～2℃，则这一天的温差是__。

A.1℃ B.-1℃ C.5℃ D.-5℃

【解析】本题主要考查有理数的减法。此问题中的温差是指最高温度与最低温度的差，所以这一天的温差是2-（-3）=2+3=5。故选C。

【点评】计算温差，实际上就是有理数的减法运算。掌握好有理数减法运算是关键。

变式2（2019·金华）某地一周前四天每天的最高气温与最低气温如下表，则这四天中温差最大的是（ ）。

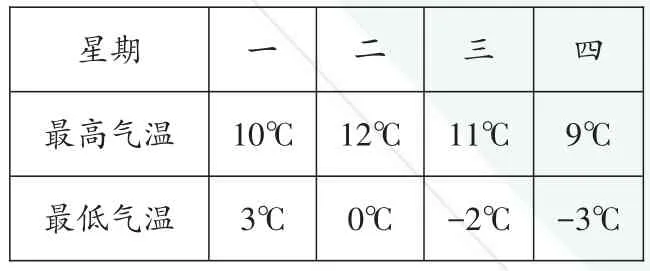
一二三四星期最高气温最低气温10℃3℃12℃0℃11℃-2℃9℃-3℃

A.星期一 B.星期二

C.星期三 D.星期四

【解析】比较每天的温差大小即可。选C。

考点3 科学记数法

科学记数法是将绝对值较大或较小的数表示成比较方便简洁的形式：a×10n。其中1≤既可以是正整数，也可以是负整数。确定n的值时一定要数清楚小数点移动的位数。

例3（2019·自贡）近年来，中国高铁发展迅速，高铁技术不断走出国门，成为展示我国实力的新名片。现在中国高速铁路营运里程将达到23000公里，将23000用科学记数法表示应为（ ）。

A.2.3×104B.23×103

C.2.3×103D.0.23×105

【解析】根据科学记数法定义求解。选A。

【点评】正确表示出a与n的值是关键。

变式3（2018·河南）据统计，2017年河南省在线政务应用的网民规模达3183万人，数据“3183万”用科学记数法表示为（ ）。

A.3.183×103B.0.3183×108

C.3.183×107D.31.83×106

【解析】本题需将“3183万”中的“万”先进行转化。将文字转化成数字，“万”表示的是104，那么3183万=3183×104。然后根据科学记数法的定义可知：3183万=3183×104=3.183×107。故选C。

考点4 利用数轴，数形结合

例4（2018·贵阳）如图1，数轴上的单位长度为1，有三个点A、B、C。若点A、B表示的数互为相反数，则图中点C对应的数是（ ）。

图1

A.-2 B.0 C.1 D.4

【解析】由相反数在数轴上的定义，可知原点位置是A、B中点。故点C对应的数是1。选C。

【点评】此题主要考查数轴三要素的确定。根据两点间的距离确定原点位置，然后通过单位长度来解决。

变式4（2019·枣庄）点O、A、B、C在数轴上的位置如图2所示，O为原点，AC=1，OA=OB。若点C所表示的数为a，则B点所表示的数为（ ）。

图2

A.-（a+1） B.-（a-1）

C.a+1 D.a-1

【解析】点B所表示的数与点A所表示的数互为相反数，而点A所表示的数为a-1，故选B。