综放开采顶煤采出率预测模型的构建与应用
2019-10-21朱帝杰陈忠辉
朱帝杰,陈忠辉
(1.太原理工大学 矿业工程学院,山西 太原 030024; 2.太原理工大学 原位改性采矿教育部重点实验室,山西 太原 030024; 3.中国矿业大学(北京) 力学与建筑工程学院,北京 100083)
综放开采作为目前我国厚煤层开采的主要技术,其最终目的是通过提高顶煤采出率、降低含矸率,使综采效益达到最优。为此,许多学者对综放开采相关规律做了大量研究[1-2]。白义如等[3]结合工程实际,利用相似模拟试验的研究方法确定了白草峪井田5号煤层的分层方法以及最佳采放比;邵小平等[4]采用薄板破断理论,通过一定简化建立了急斜煤层顶板岩层的薄板力学模型,确定了急斜煤层综放开采工作面合理段高判别式,并以此计算了不同倾角煤层的合理段高极值;VAKILI A等[5]综合BCCM等4种数值模型,结合工程实际较好的分析了综放开采顶煤的冒放机理,明确了影响顶煤冒放性的6种指标,提出了一种新的顶煤冒放性及顶煤采出率评价准则;KAREKAL S等[6]将基于光滑粒子流体动力学的无网格连续数值方法应用于模拟长壁开采的岩石垮落过程,通过与传统基于网格的数值模拟方法对比,指出该方法具有与其他数值方法兼容性好、计算效率高的优点,尤其适用于模拟断层结构及破碎的大变形和块体流动等问题;MANOJ KHANAL等[7]利用有限元软件模拟了直接顶以及不同层位顶煤的垮落模式,指出其具有相似性,分析了顶板强度及硬度对顶煤采场不同位置支撑压力的影响;来兴平等[8]结合理论分析、数值模拟和现场实测等方法分析了急斜特厚煤层覆层类椭球体结构形成过程与局部化动态演化规律,指出顶煤与上覆残留煤矸复合形成非对称“拱结构”并演化为典型倾斜椭球体结构;BASARIR H等[9]结合Soma Eynez煤矿实际,利用FLAC3D分析了巷道附近的应力分布,并指出分析结果可用于进一步分析回风巷道的稳定性;蒋金泉等[10]对颗粒状散体介质离散元软件进行再开发,模拟了不同放煤步距条件下的破碎顶煤与直接顶的放出规律,给出了顶煤厚度为2~3 m时的合理放煤步距并用于指导实际生产;黄炳香等[11]采用散体模型试验分析了不同放煤步距、不同顶煤块度对煤矸砂流动状态和混矸程度的影响,给出了不同煤矸块度条件下的放煤步距选取原则;陈庆丰等[12]结合平朔矿区生产实际,通过相似模拟试验研究了顶煤采出率与含矸率的相互关系,指出实际生产时可将煤流中的矸石比例达到20%作为终止放煤的依据;王家臣等[13]利用自主研发的顶煤运移跟踪仪对顶煤采出率进行了现场观测,指出对于一般条件的放顶煤工作面,可用70%作为顶煤采出率的基本估计;YANG Shengli等[14]运用PFC3D软件分析了不同煤层倾角条件下的顶煤放出体及煤矸分界线形态,并结合模型试验和现场观测等方法分析了不同层位顶煤采出率的大小,指出顶煤采出率随距离底板高度的增加而减小。已有研究成果对深入理解综放开采顶煤放出规律具有重要意义,但同时可以看出,目前的研究(特别是对放出体形态和顶煤采出率的研究)还多局限于数值模拟和模型试验等方法,仅有的理论研究仍然停留在经典椭球体理论[15-16],总体进展缓慢,而且对于何时终止放煤也没有一个具体标准。
基于上述分析,结合综放开采时单个煤块和矸石的流动往往具有随机性的客观事实,于斌等[17-18]初次尝试利用随机介质理论研究了综放过程中顶煤放出体和煤矸分界线的形态特征,并进行了模拟验证。笔者尝试将随机介质理论引入到综放开采顶煤回收研究,推导了煤矸分界线和放出体方程,进一步研究了放出体的动态演化规律,建立了顶煤采出率与含矸率的理论计算模型,据此讨论了两者的相互关系;然后结合同煤集团塔山矿生产实际,通过模型试验和现场实测,研究了顶煤采出率与含矸率的相互关系,给出了可用于指导实际生产的放煤终止原则。研究成果对于推动综放开采的理论研究和指导实际生产具有借鉴意义。
1 理论分析
随机介质理论由波兰学者LITWINISZYN[19]于20世纪50年代提出,最初用于描述干砂的流动和预测颗粒流放出体形状,国内外学者不断发展完善[20-22]。该理论在金属矿开采中的应用愈加频繁,理论体系也日趋成熟[23-24],已经成为除椭球体放矿理论之外的又一崩落法放矿分析方法,但在厚煤层综放开采中还鲜有涉及。
综放开采的移架过程导致顶煤和顶板破碎成结构极为复杂的多孔隙散体,该散体结构在重力作用下发生垮落,忽略垮落过程中顶煤和矸石的瞬时松散效应,将其简化为连续流动的随机介质,利用概率统计和微积分方法推导出煤矸分界线和放出体方程,建立顶煤采出率与含矸率理论计算模型,并据此研究顶煤放出体形态演化规律以及顶煤采出率与含矸率的相互关系。该研究过程假定:
(1)移架过程中,顶煤和顶板在重力和震动作用下充分破碎。
(2)忽略顶煤和矸石密度、块度以及孔隙等因素的影响,将破碎顶煤及矸石简化为可在重力作用下连续流动的随机介质。
(3)周期性放煤时,将上一次放煤结束时形成的煤矸分界线作为下一次放煤的起始煤矸分界线,即假设在移架过程中无顶煤和矸石垮落。
1.1 公式推导
以综放支架放煤口中心为坐标原点建立二维平面坐标系,如图1所示。在放煤过程中,标志层逐渐沉降为漏斗状曲线并随放出顶煤量不断变化,将沉降曲线极值点连线定义为偏移曲线(图1红色虚线),统计多组数值模拟不同高度标志层沉降曲线极值点在x方向的偏移量,结果表明该偏移量呈一定规律,结合文献[23]与图1坐标系,利用综合优化分析计算软件平台1stOpt对各偏移量进行最小二乘回归拟合,结果表明该偏移曲线可表征为
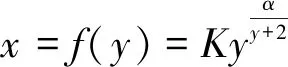
(1)
式中,K为尾梁影响系数;α为煤矸散体流动参数。
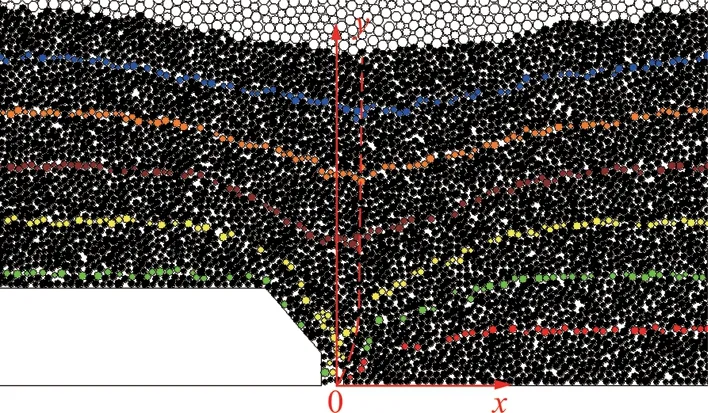
图1 理论推导坐标系Fig.1 Coordinate system for theoretical derivation
结合文献[23]得煤矸散体颗粒移动概率密度方程:
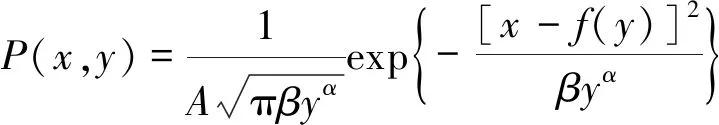
(2)
式中,β为煤矸散体流动参数;A为尾梁平均切余系数,由式(3)得到:
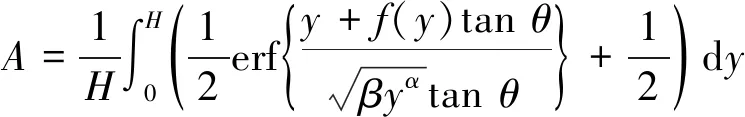
(3)
式中,H为煤层厚度;θ为尾梁倾角。
考察某一点(x,y),以该点为中心取一δ邻域,设该邻域长度为l,由式(2)得δ邻域内煤矸散体下移概率:
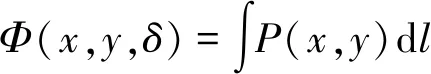
(4)
设单位时间内放煤口放出煤矸散体量为s(s为常数,表示放出体纵剖面面积),煤矸散体平均铅直下降速度为vy,根据统计学知识,单位时间内流入δ邻域(足够小)的煤矸散体量等于流出量,即
Φ(x,y,δ)s=P(x,y)ls=lvy
(5)
由式(5)得铅直移动速度方程:
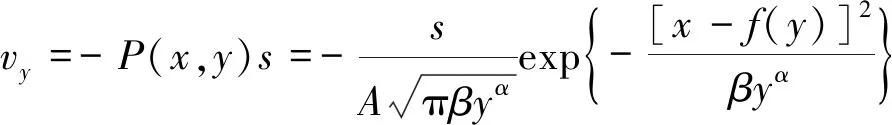
(6)
式中,负号表示速度方向与坐标增量方向相反。
设想以点(x,y)为中心任取一线单元,为保持流动连续性,单位时间内流出该线单元的面积量与流进量应相等(即实际工程中单位时间内流出某一水平面的煤矸散体量与流进量相等),根据二维流体流动的连续性方程得平均水平下降速度:
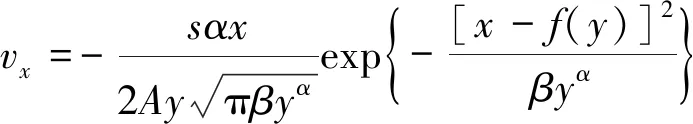
(7)
对于任一固定点,颗粒经过该点时的移动迹线之切线,应与该点速度方向共线,故有dx/dy=vx/vy,将式(6),(7)代入此关系式,积分得煤矸颗粒移动迹线方程:
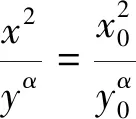
(8)
设y0层面上某散体颗粒坐标为A0(x0,y0),当放煤口放出煤矸量S时,该颗粒下移到A(x,y)位置,颗粒在下移过程中应满足dy/dt=vy,将式(6),(8)代入该关系式得
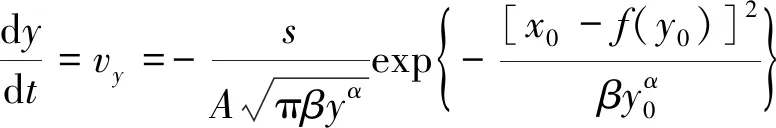
(9)
将式(9)沿颗粒移动迹线积分整理得
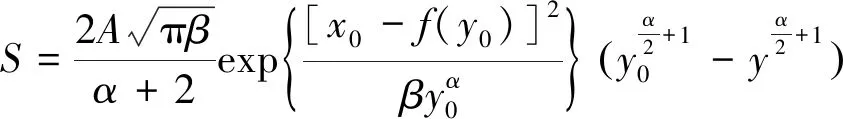
(10)
联立式(8),(10),整理得煤矸y0层面沉降曲线方程:
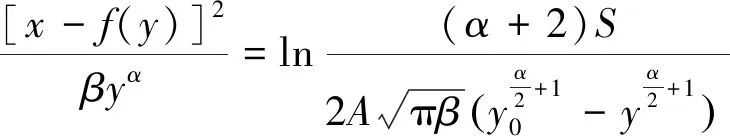
(11)
当颗粒A0(x0,y0)刚好移到放煤口时,此时对应的放出量S0定义为A0点的达孔量,在式(10)中令y=0,并去掉x0,y0的脚标,得煤矸颗粒达孔量方程:
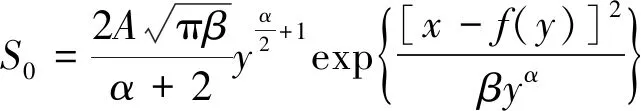
(12)
由式(12)可知,对于任一高为y的层面,在x=f(y)点颗粒的达孔量S最小,因此放出体顶点的坐标位置为[f(yH),yH]。当放出体顶点到达放煤口时,放出量为
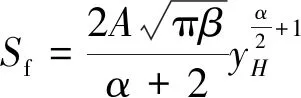
(13)
式中,yH为放出高度(铅直高度)。
联立式(11),(13),并将y0,yH替换为煤层厚度H,得煤矸分界线方程:
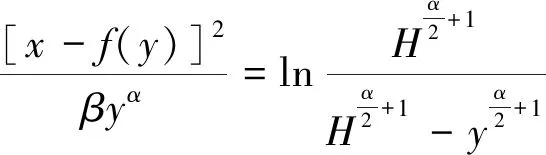
(14)
放出体表面是达孔量场的等值面,联立式(12),(13),整理得放出体方程:
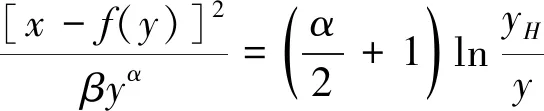
(15)
1.2 煤矸散体流动参数确定
在模型中铺设多层带序号直径0.004 m的白色巴厘石标志颗粒,其层间距0.026 m,水平间距0.015 m。为最大程度减小模型侧壁影响,标志颗粒铺在模拟煤层走向中部,如图2所示,具体材料参数见模型试验部分。根据理论推导坐标系确定标志颗粒坐标,模拟放煤至顶层标志颗粒高度,统计放出的标志颗粒,反推放出体形态,并用式(15)回归拟合,从而确定煤矸散体流动参数α,β和尾梁影响系数K。
以顶煤厚0.13 m为例,放出体试验形态及回归拟合结果如图3所示,参数拟合结果为:α=1.60,β=0.40、尾梁影响系数K=0.20;同理得顶煤厚0.26 m时,α=1.52,β=0.28,K=0.14;顶煤厚0.39 m时,α=1.46,β=0.21,K=0.08。
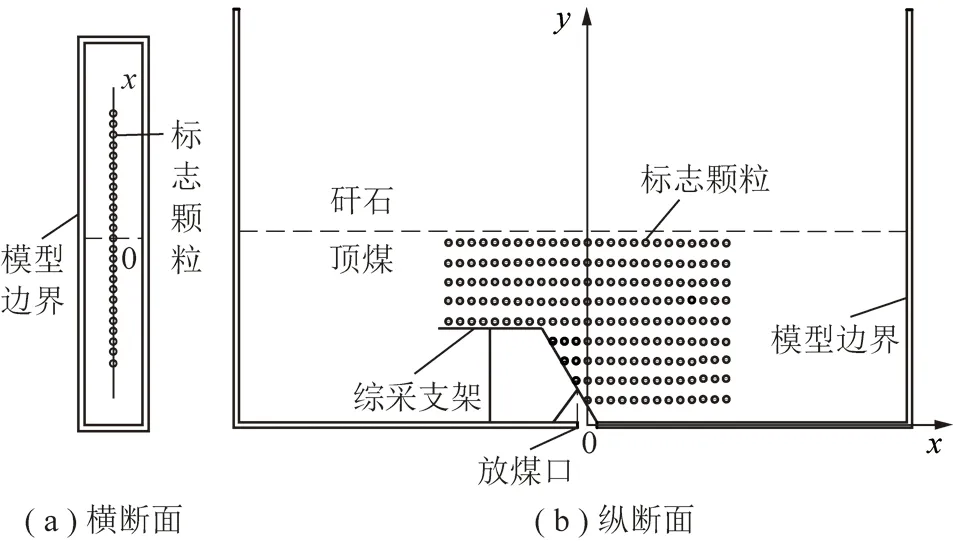
图2 标志颗粒布置示意Fig.2 Layout of marked particles
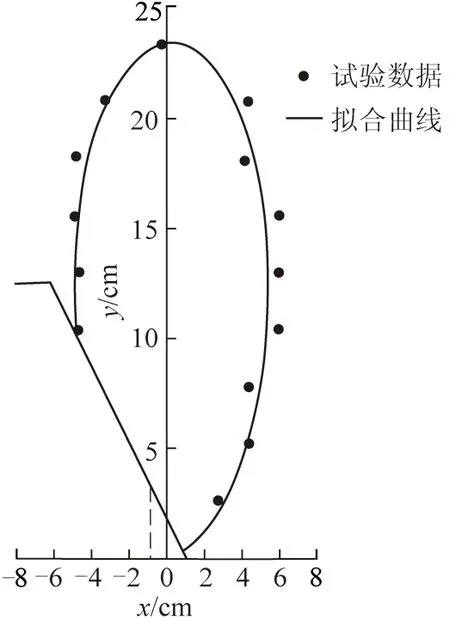
图3 顶煤放出体回归拟合Fig.3 Regression fitting of top coal drawing body
1.3 顶煤放出体动态演化
结合同煤集团塔山矿8102工作面实际工况,取综放支架高度h=3.5 m,尾梁倾角θ=60°,根据所推放出体方程画出不同顶煤厚度、不同放煤程度时的顶煤放出体形态,分析其发育特征,如图4,5所示。
由图4可知,不同顶煤厚度条件下的放出体演化特征整体相似:对于某一顶煤厚度,放出体高度较小时,放出体轴偏角(放出体长轴即虚线与y轴夹角)较大,放出体形状呈尾梁切割类圆形,此时经典椭球体理论的适用性较低;随着放出体高度的增加,放出体轴偏角逐渐减小,即逐渐向煤壁方向倾斜,其形状逐渐过渡为尾梁切割类椭圆,椭球体理论的适用性逐渐增强。由图5可知,不同顶煤厚度条件下的放出体演化特征又有所差异:当放出体高度相等时,顶煤越厚,其对应的放出体轴偏角及放出量(放出体面积)越小,放出体形状较顶煤薄时更接近椭圆。
1.4 顶煤采出率与含矸率关系
依据图6定义顶煤储量为(H-h)L,则相应有:顶煤采出率=S2/[(H-h)L]、含矸率=S1/(S1+S2)。取放煤步距L=0.8 m,分别讨论顶煤厚3.5,7.0和10.5 m三种情况下顶煤采出规律。限于篇幅,现仅将顶煤厚3.5 m时的矸石放出量、顶煤放出量以及含矸率、顶煤采出率计算结果列出,见表1。
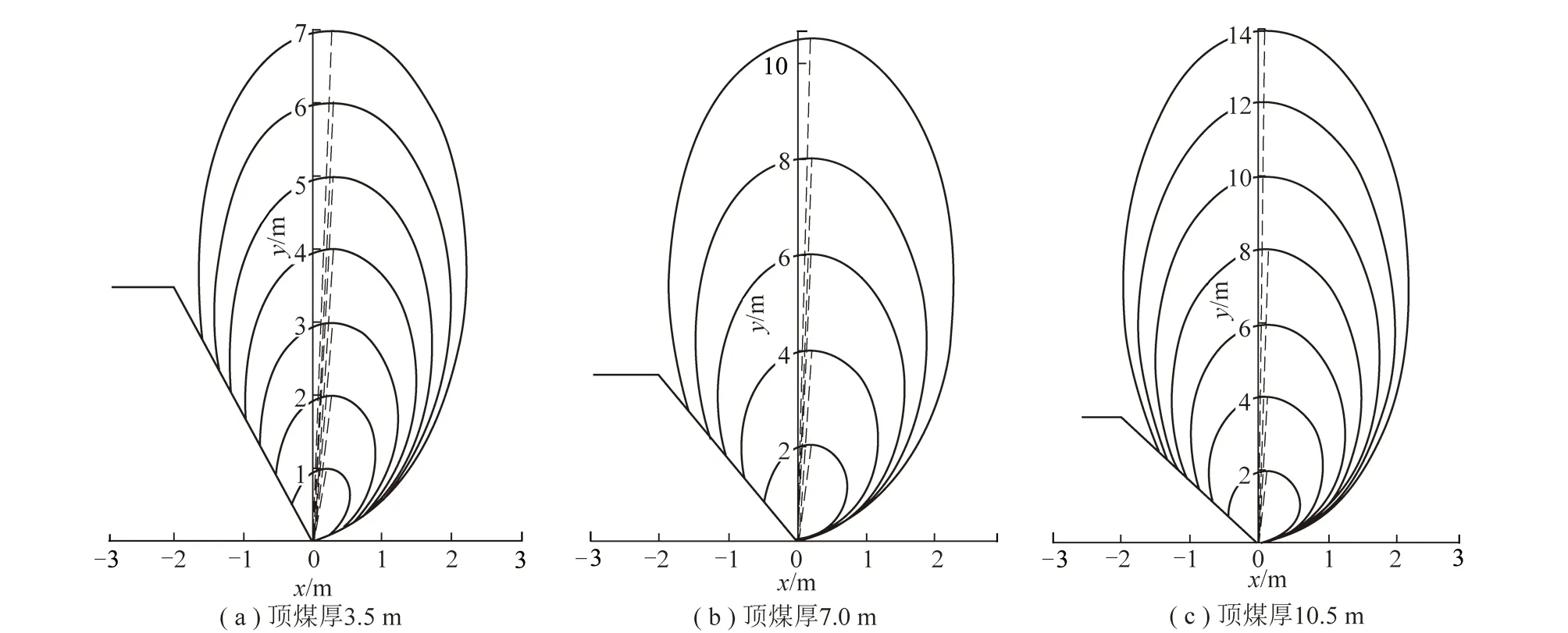
图4 放出体演化过程Fig.4 Developing process of the drawing body
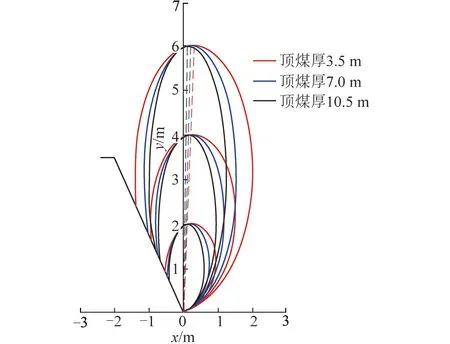
图5 放出体形态对比Fig.5 Shape contrast of the drawing body
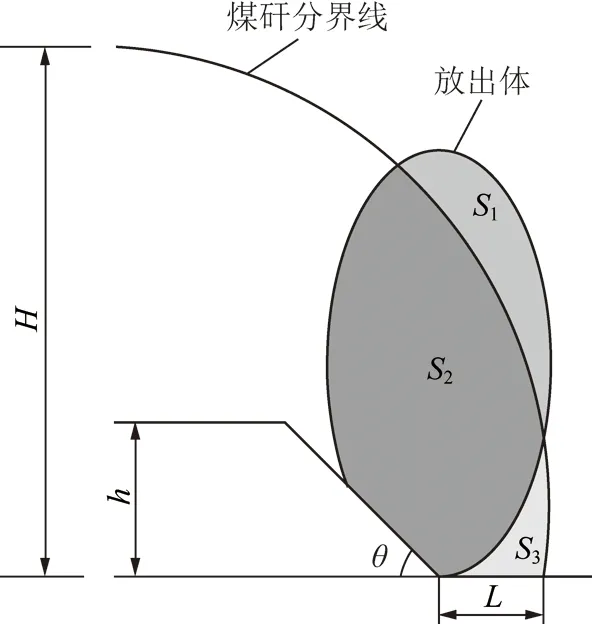
图6 顶煤采出率与含矸率理论计算模型Fig.6 Theoretical model for calculating top-coal recovery ratio and rock-mixed ratioH—煤层厚度;h—支架高度;L—放煤步距;S1—矸石放出量;S2—顶煤放出量;S3—未放出煤量
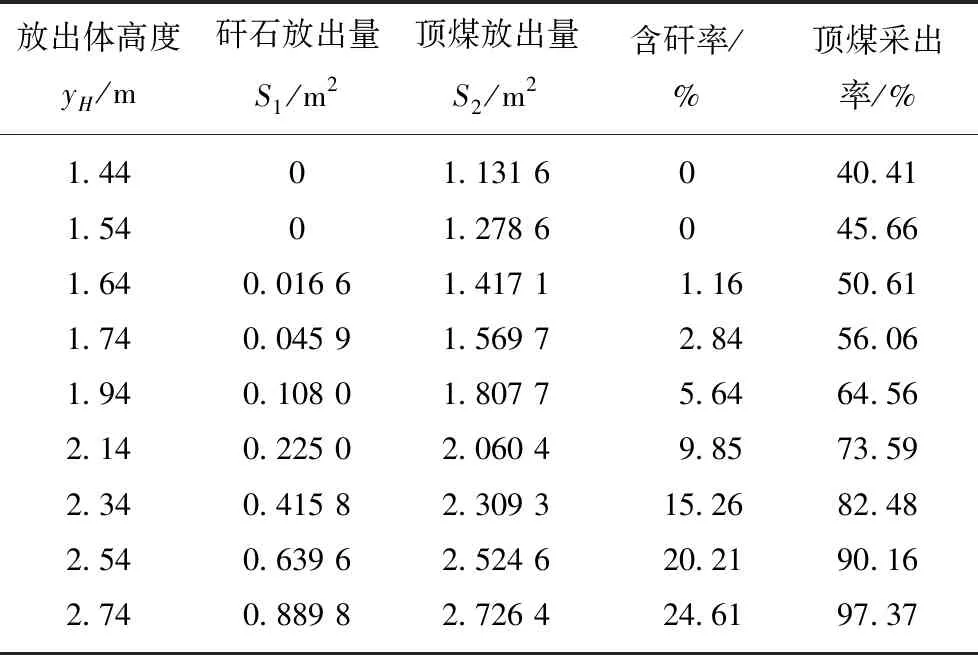
放出体高度yH/m矸石放出量S1/m2顶煤放出量S2/m2含矸率/%顶煤采出率/%1.4401.131 6040.411.5401.278 6045.661.640.016 61.417 11.1650.611.740.045 91.569 72.8456.061.940.108 01.807 75.6464.562.140.225 02.060 49.8573.592.340.415 82.309 315.2682.482.540.639 62.524 620.2190.162.740.889 82.726 424.6197.37
当顶煤放出体与煤矸分界线刚好相切时,继续放煤便会有矸石混入,取固定采高h=3.5 m,分别计算不同顶煤厚度条件下放煤至开始见矸时的顶煤放出体高度以及对应顶煤采出率,计算结果见表2。
表2 开始见矸时的放出体高度和顶煤采出率
Table 2 Drawing body height and top coal recovery ratio when rock begins to intrude into top coal
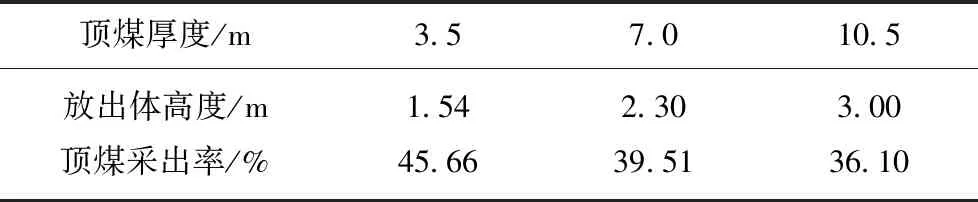
顶煤厚度/m3.57.010.5放出体高度/m1.542.303.00顶煤采出率/%45.6639.5136.10
将不同顶煤厚度条件下的含矸率与顶煤采出率变化关系绘制成曲线,如图7所示。
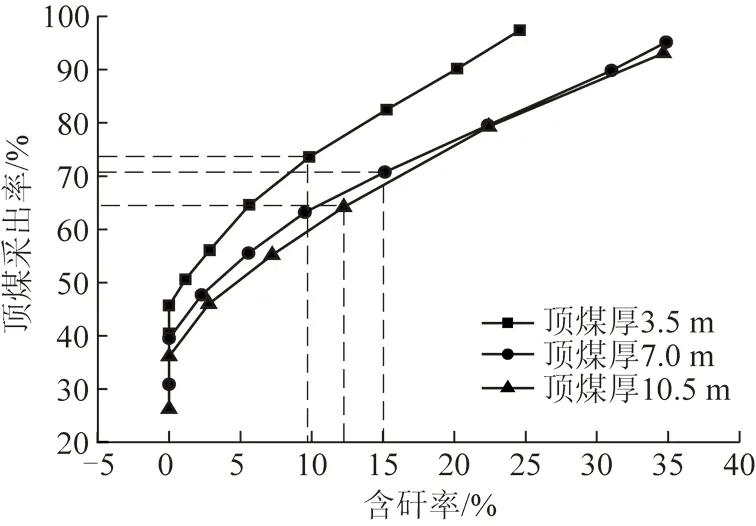
图7 顶煤采出率与含矸率关系(理论)Fig.7 Relation between top coal recovery ratio and rock-mixed ratio (theoretical calculation)
在放煤初期,放出体与煤矸分界线相离,含矸率为0,所放为纯顶煤,对应顶煤采出率定义为纯顶煤采出率;当放出体与煤矸分界线相切时,恰好见矸,继续放煤,放出体与煤矸分界线相交,矸石开始混入且混入速率越来越快。由表2及图7可知:① 顶煤厚3.5 m,当放出体高度达到1.44 m时,对应纯顶煤采出率为40.41%。当放出体高度达到1.54 m时,恰好见矸,对应顶煤采出率为45.66%。继续放煤,矸石开始混入但速率较慢,顶煤采出率达到65%之前,含矸率始终低于6%。当顶煤采出率增至73.59%时,含矸率为9.85%,此后若继续放煤,含矸率快速增加,而顶煤采出率则增加缓慢,将此时的顶煤采出率、含矸率分别定义为顶煤拐点采出率和拐点含矸率(下同);② 顶煤厚7.0 m,当放出体高度达到2.0 m时,对应纯顶煤采出率为30.84%。当放出体高度达到2.30 m时,恰好见矸,对应顶煤采出率为39.51%。继续放煤,矸石开始混入,顶煤拐点采出率为70.74%,拐点含矸率为15.13%;③ 顶煤厚10.5 m,当放出体高度达到2.5 m时,对应纯顶煤采出率为26.23%。当放出体高度达到3.00 m时,恰好见矸,对应顶煤采出率为36.1%。继续放煤,矸石开始混入。顶煤拐点采出率为64.18%,拐点含矸率为12.26%。
综上可知,3种顶煤厚度条件下的数值在某些关键量值方面有所差异:顶煤越薄,开始见矸的顶煤采出率及顶煤拐点采出率越大。但无论哪种顶煤厚度,顶煤采出率与含矸率均呈非线性增大关系,拐点含矸率较接近,其范围为9%~16%。
2 模型试验
以同煤集团塔山矿8102工作面为背景,通过室内模型试验分析了顶煤采出率与含矸率的关系,以验证随机介质理论的可行性。
2.1 工程背景及试验设置
塔山矿8102工作面长231 m,采高3.5 m,走向长1 700 m,煤层均厚13.9 m,埋深418~552 m,采放比约1∶2.9,煤层密度1 450 kg/m3,抗压强度平均32 MPa;直接顶均厚8 m,基本顶均厚20 m,抗压强度10~50 MPa不等;该工作面使用ZF10000/25/38低位放顶煤液压支架,其初撑力7 730 kN,工作阻力10 000 kN,高2.5~3.8 m,长5.42 m、宽1.75 m,采煤工艺为头尾端头斜切进刀,双向割煤,循环进度0.8 m,采放工艺为一刀一放多轮顺序放煤,头尾过渡支架不放煤。
基于上述工程背景,模型试验相关参数设置如下:试验几何相似比为1∶27;支架高度0.13 m,尾梁倾角60°;模拟顶煤的黑色巴厘石粒度为0.002~0.008 m,以0.002 m为一个数量级,主要集中在0.004 m,其密度为1.4×103kg/m3;模拟直接顶的巴厘石粒度为0.008~0.016 m,密度为2 450 kg/m3;模拟基本顶的巴厘石粒度为0.016~0.024 m,密度为2 520 kg/m3;直接顶厚为0.25 m,基本顶厚为0.15 m,试验一刀进尺0.03 m,设置0.13,0.39 m两种顶煤厚度,对应每刀顶煤体积分别为9.29×10-4m3和2.29×10-3m3。
2.2 试验结果分析
限于篇幅,现仅将顶煤厚0.13 m条件下的部分试验过程图列出,如图8,9所示。
称量并计算每刀每次放出的煤矸量,结果见表3。
根据2种顶煤厚度条件下的煤矸数据,计算出顶煤采出率、含矸率平均值,并绘制曲线如图10所示。由图10可知,顶煤采出率与含矸率均呈非线性增大关系;顶煤厚0.13 m开始见矸的顶煤采出率为17.43%,顶煤拐点采出率为77.85%,拐点含矸率为7.19%;顶煤厚0.39 m开始见矸的顶煤采出率为15%,顶煤拐点采出率为73.59%,拐点含矸率为8.07%。
可见模型试验整体上符合“顶煤越薄,开始见矸的顶煤采出率及顶煤拐点采出率越大”的理论分析结果,且试验与理论所得顶煤拐点采出率误差在10%以内,拐点含矸率误差在5%以内,表明将随机介质理论引入到综放开采顶煤放出规律研究是可行的。
3 现场实测
以同煤集团塔山矿8101,8102和8111综放工作面为监测对象,结合地质报告,去除工作面割煤量和煤层夹矸量,整理计算出工作面顶煤采出率与含矸率,见表4。

图8 顶煤厚0.13 m放煤过程Fig.8 Drawing process under 0.13 m top coal thickness condition

图9 煤矸比例变化(第6刀)Fig.9 Variation in the ratio of top coal and rock in the sixth drawing process
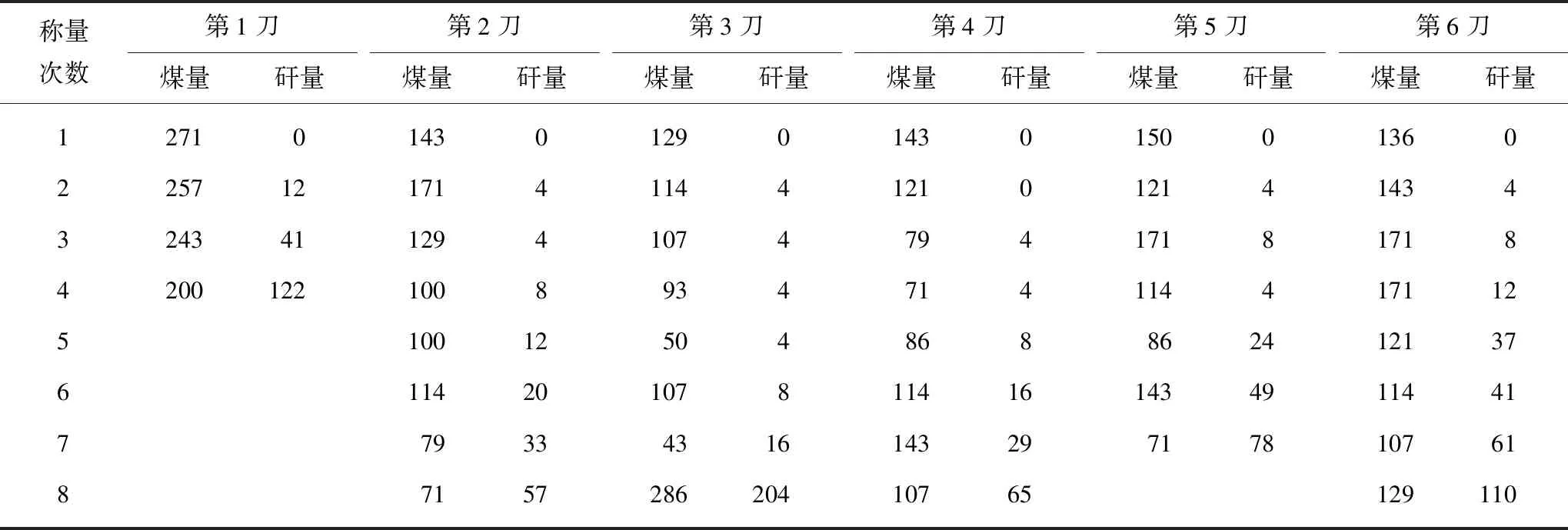
表3 顶煤厚0.13 m试验煤矸数据
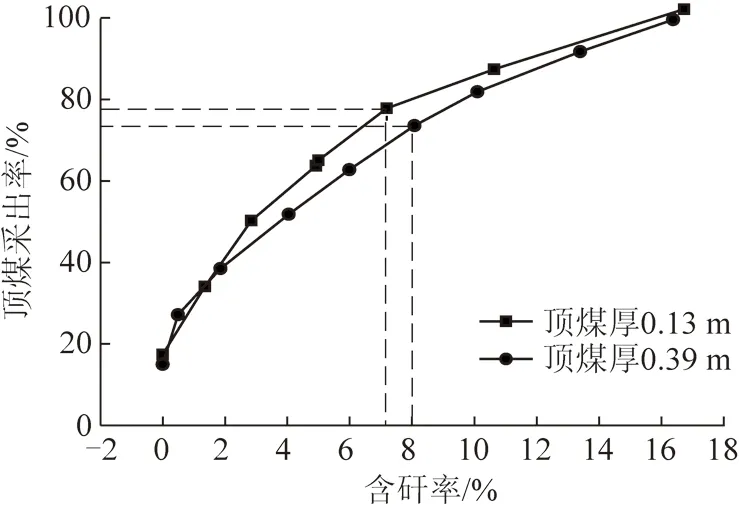
图10 顶煤采出率与含矸率关系(试验)Fig.10 Relation between top coal recovery ratio and rock-mixed ratio (model experiment)
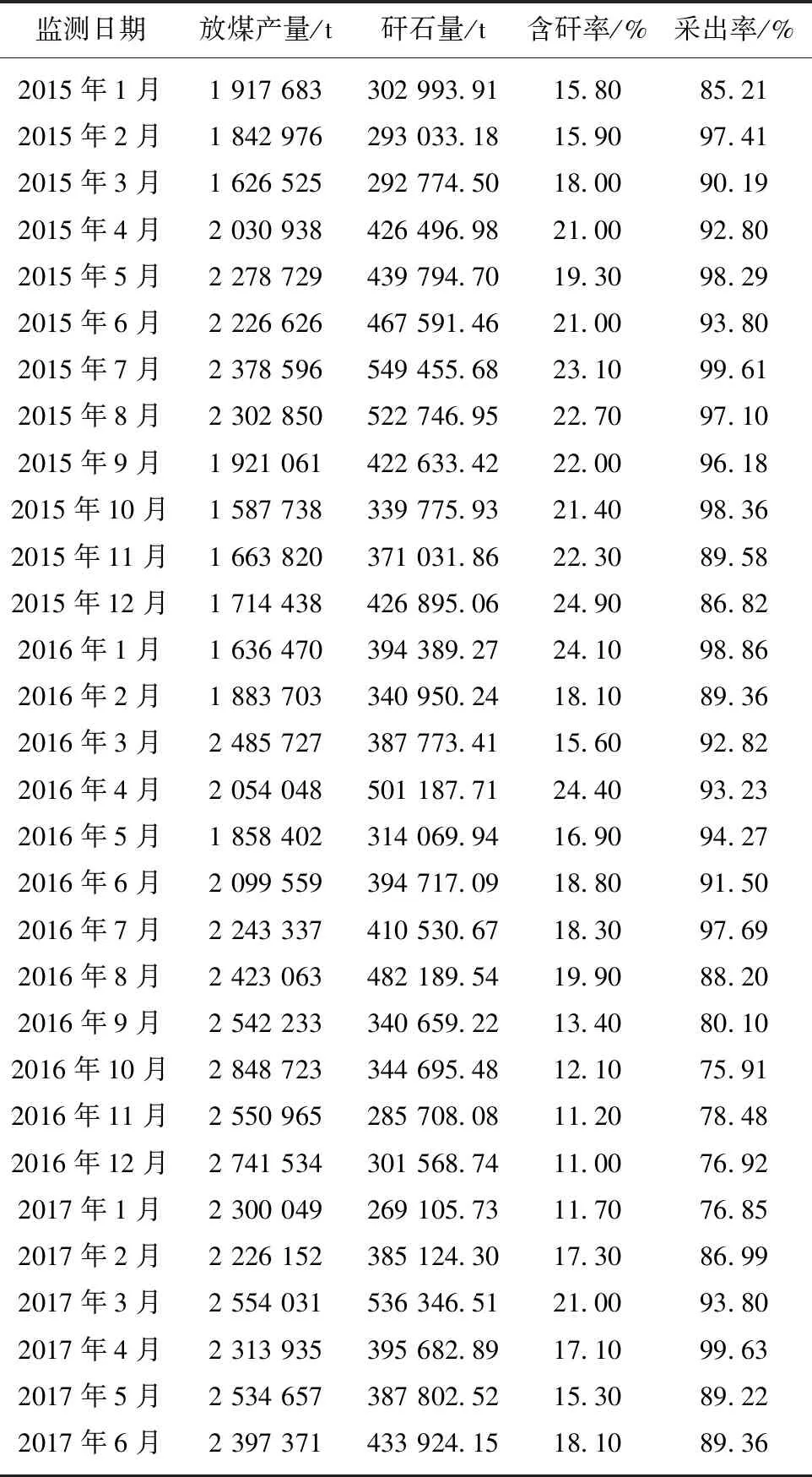
监测日期放煤产量/t矸石量/t含矸率/%采出率/%2015年1月1 917 683302 993.9115.8085.212015年2月1 842 976293 033.1815.9097.412015年3月1 626 525292 774.5018.0090.192015年4月2 030 938426 496.9821.0092.802015年5月2 278 729439 794.7019.3098.292015年6月2 226 626467 591.4621.0093.802015年7月2 378 596549 455.6823.1099.612015年8月2 302 850522 746.9522.7097.102015年9月1 921 061422 633.4222.0096.182015年10月1 587 738339 775.9321.4098.362015年11月1 663 820371 031.8622.3089.582015年12月1 714 438426 895.0624.9086.822016年1月1 636 470394 389.2724.1098.862016年2月1 883 703340 950.2418.1089.362016年3月2 485 727387 773.4115.6092.822016年4月2 054 048501 187.7124.4093.232016年5月1 858 402314 069.9416.9094.272016年6月2 099 559394 717.0918.8091.502016年7月2 243 337410 530.6718.3097.692016年8月2 423 063482 189.5419.9088.202016年9月2 542 233340 659.2213.4080.102016年10月2 848 723344 695.4812.1075.912016年11月2 550 965285 708.0811.2078.482016年12月2 741 534301 568.7411.0076.922017年1月2 300 049269 105.7311.7076.852017年2月2 226 152385 124.3017.3086.992017年3月2 554 031536 346.5121.0093.802017年4月2 313 935395 682.8917.1099.632017年5月2 534 657387 802.5215.3089.222017年6月2 397 371433 924.1518.1089.36
根据实测数据拟合出顶煤采出率与含矸率的关系曲线,据此确定实际生产拐点采出率与拐点含矸率,如图11所示。
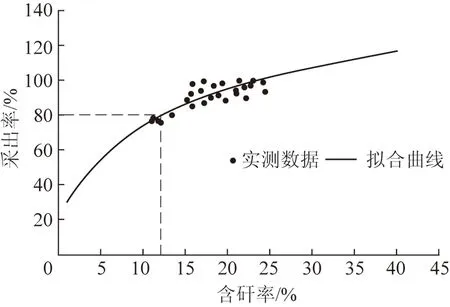
图11 现场实测采出率与含矸率关系Fig.11 Relation between recovery ratio and rock-mixed ratio obtained from the filed observation
由图11可知:根据现场实测所得数据拟合出的采出率与含矸率关系与理论分析和模型试验所得趋势一致,且现场实测所得拐点采出率约为80%,对应拐点含矸率约为12%,处于理论和试验所得9%~16%范围内,进一步证明了理论分析的可行性。
4 结 论
(1)将随机介质理论引入到综放开采顶煤采出研究,推导了煤矸分界线和放出体方程,分析了顶煤放出体的演化特征,建立了顶煤采出率与含矸率的理论计算模型,讨论了顶煤采出率与含矸率的关系,并通过试验和现场实测验证了理论分析的可行性,具有一定理论和工程意义。
(2)放煤过程中,放出体轴偏角随放出体高度增加而逐渐减小,即放出体逐渐向煤壁方向倾斜,其形状由尾梁切割类圆形过渡为类椭圆;采高和放出体高度相等时,顶煤越薄,放出体轴偏角及放出量越大。
(3)顶煤采出率与含矸率呈非线性增大关系,提出顶煤拐点采出率和拐点含矸率的概念;针对某一采高,顶煤越薄,对应开始见矸时的顶煤采出率和顶煤拐点采出率越大;生产实际中无论顶煤多厚,均可将含矸率9%~16%作为放煤终止依据。
