基于分形理论的岩石裂隙非线性渗流各向异性研究
2019-10-20王慧苏永军王凤瑞
王慧 苏永军 王凤瑞

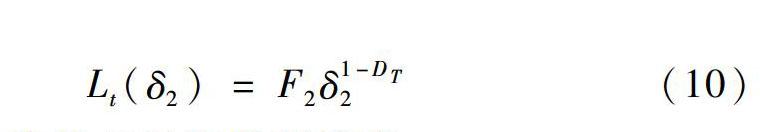

摘要:针对裂隙岩体非达西渗流问题,开展了不同粗糙裂隙非线性渗流特性的研究。将完整的方形岩块采用劈裂法制成裂隙试件,用三维光学扫描系统量测裂隙表面形貌,并采用Kulatilake提出的自仿射分形维度方法计算表面的分形维度来表征粗糙表面的各向异性特征。根据裂隙流的曲折效应,在Forchheimer定律基础上,提出了水文弯曲度和表面分形幂律关系来表征非线性特点,并由此提出了新的粗糙裂隙非线性分形模型。对各组裂隙试件在2个方向(0°,90°)上进行饱和渗流试验,发现流动符合Forchheimer定律且存在各向异性特点,最后由分形模型,提出了区分达西流与Forchheimer流的新判据。
关键词:岩石裂隙; 非线性渗流; 分形维度; Forchheimer定律; 各向异性; 临界雷诺数
中图法分类号:P641.2文献标志码: ADOI:10.16232/j.cnki.1001-4179.2019.02.031
1研究背景
漫长的地质作用和人类活动造成岩体被大量的断层、裂隙切割,这些结构面及其构成的网络成为地下水流动的主要通道,并由此控制着岩体的渗透特性。在岩体水力学研究中,通常将结构面概化为2块光滑的平行板,通过理论和试验得到著名的立方定律。由于实际结构面粗糙起伏、零星接触或含有充填物等,许多学者据此提出各种修正模型。
在某些工程中,如河谷深厚覆盖层建坝、低渗透油气井开采、煤矿瓦斯突出等[1]都会出现高水力梯度现象,这时流体流动的机制和规律将发生重大改变,用立方定律或其修正模型会造成较大的偏差。一般引用多孔介质的非线性渗流模型Forchheimer定律[2]来描述这种渗流行为
▽P=AQ+BQ 2(1)
式中,▽P为单位渗流长度的压力差,Q为通过裂隙的流量,A和B分别为黏性系数和惯性系数。
Zimmerman等[3]通过试验和数值的方法,观察到雷诺数Re>20时,粗糙裂隙的Forchheimer流现象;Zhang等[4]探讨了不同围压下,粗糙裂隙线性和非线性流动特性;Zhou等[5]利用不同围压的压水试验,解释了Forchheimer流系数A和B的物理意义,及内部过渡机制,但对裂隙面粗糙性对非线性流动的影响没有详细阐明。Chen等评价了Forchheimer判据方程的系数[6]。金毅等[7]从细观层面上指出粗糙几何对裂隙流的影响表现在三个方面:① 流体内部的摩擦效应;② 裂隙面的曲折效应;③ 局部粗糙度效应。Tsang等[8]认为裂隙面的粗糙性会引发流动的曲折性;肖维民等[9]引入曲折因子描述这种流动的曲折现象。
自分形几何被B.B.Mandelbrot提出以后,谢和平等[10]首先将其引入到裂隙粗糙度的描述,后来又用来描述岩体断裂面渗流特征[11];Murata等[12]研究了分形参数对曲折效应的影响;王刚等[13]提出了考虑分形特征的节理面渗流公式;Ju等[14]对不同分形维度粗糙单裂隙物理模型进行水渗流试验,阐明了粗糙结构对渗流的影响;Develi等[15]对7种人工张拉型裂隙面进行饱和渗流试验,并用分形维度描述粗糙度,研究了粗糙度、各向异性和法向应力对渗流特征的影响。
本文从曲折效应对裂隙流非线性作用强度和方式入手,并结合裂隙自仿射分形特点,推导了粗糙裂隙非线性分形模型。并结合渗流试验,分析了Forchheimer流的规律和各向异性,并验证了新模型。
2粗糙裂隙非线性分形模型
Forchheimer流动定律包含两个部分:线性部分AQ和非线性部分BQ 2,体现出达西渗流和非达西渗流。在低流速阶段,一般可用立方定律描述流量和压力的线性关系,则黏性系数A可表示为
A=12μwe 3h(2)
式中,μ为流体的黏性系数,w为裂隙的宽度,eh为水力开度,是在初始阶段根据立方定律反求而得,eh=(12μQ/w/▽P)1/3。
惯性系数B体现了渗流曲线偏离线性段的程度。Schrauf等[2]通过量纲分析,提出
B=bDρe 3hw 2(3)
式中,ρ为流体密度,bD是与裂隙面结构特征有关的参数。Chen等[6]用绝对粗糙度描述裂隙面几何特征,提出的双参数模型为
bD=a(ξ2eh) b(4)
式中,a和b为拟合参数。但仅仅用绝对粗糙度ξ表征裂隙面粗糙程度的影响,不能反映流动的曲折性和各向异性。郭建春等[16]通过数值方法研究了裂隙流的非达西效应,结果表明表面越粗糙,隙宽分布越复杂,流动时流态将越不稳定,曲折效应将增加,在高流速下会出现涡流和回流现象,增大惯性阻力。为了表征曲折性的影响,提出如下幂律关系
bD=cτ aτ bs(5)
式中,a,b和c为拟合参数;τ为水文弯曲度,定义为流体实际渗流路径长度Lt与沿裂隙水头压力梯度方向的水平长度Lc之比。τs为裂隙面曲折率,定义为裂隙面表面积As与投影面积Ac之比。对于具有分形特征的裂隙,测度F(δ)与测量尺度δ存在如下关系
F(δ)=F0δ(6)
式中,与分形维数D有关,即=f(D),D∈(1,3);F0为直观测度。边长为δ1的正方形网格覆盖的裂隙表面总的面积AS与δ1存在如下关系
AS=F1δ2-DS1(7)
式中,DS为裂隙面面积分形维度,对于正方形裂隙,当δ1=Lc时,将(7)式代入AS(Lc)=Ac得:
F1=ADS2c(8)
由τs的定义,有
τs=AS(δ1)Ac=(δ 21Ac)2-DS(9)
同理,对于渗流路径長度Lt同观测尺度δ2存在如下分形关系:
Lt(δ2)=F2δ1-DT2(10)
式中,DT为渗流路径长度分形维度。
当δ2=Lc时,将(10)式代入Lt(Lc)=Lc得
F2=LDTc(11)
由τ定义得
τ=Lt(δ2)Lc=(δ2Lc)1-DT(12)
分形创始人Mandelbrot建议表面分形维数可用表面某一剖线的维数加1的方法计算,故对于剖面线长度分形维数DL与面积分形维度DS存在如下关系
DS=DL+1(13)
金毅等[7]研究表明,DL≈DT,故将其与式(9)和式(12)代入式(5)中,得
bD=c(δ2Lc)a(1-Dt)(δ 21Ac)b(1-Dt)(14)
取δ1和δ2的测度为eh,同时有Ac=L 2c,代入式(14)得
bD=c(ehLc)(a+b)(1-DL)(15)
重新整理式(15),得到B新的表达式为
B=a(ehLc)b(1-DL)ρe 3hw 2(16)
式中,a和b为待定常数,可由裂隙渗透试验确定。计算时,首先获取裂隙表面数据,计算分形维度,然后通过裂隙渗透试验得到流量与压力梯度的曲线,拟合得到A和B参数,并进一步获得a和b。
3裂隙面测量与分形计算
3.1裂隙面制备
为了研究裂隙面粗糙度对流体流动的影响,需要对不同粗糙程度的岩体裂隙面进行饱和渗流试验。而天然裂隙面较难获取,因此,本次采用人工张拉裂隙试件研究裂隙中流体流动特征。将选自湖北省境内某采石场的天然花岗岩在室内加工成尺寸为150 mm×150 mm×150 mm方形試块,然后用巴西劈裂试验方法将试块劈开,制成人工张拉性节理试件。最终制备成5组不同粗糙程度的裂隙面(F1,F2,F3,F4和F5)。
3.2裂隙表面形貌测量
试验采用便携式3D CaMega光学三维扫描系统对裂隙表面三维形貌进行量测。3D CaMega光学三维扫描系统是一台非接触高精度光学扫描仪(见图1)。该系统主要由扫描控制单元、扫描镜头、转台和三脚架组成;扫描镜头安放在三角架上,三脚架可自由伸缩旋转,方便调整位置,其他部分通过USB方式连接。系统通过获取投射到物体表面的可见光光栅图像,按照条纹曲率变化形状利用相位法和三角法精确确定每一点空间坐标(X,Y,Z),形成三维点云数据,具有快速、精度高(测量精度25μm)、非接触测量等的特点。
图13D光学扫描系统示意Fig.1Stereotopometric scanning system
在实际测量过程中,测量环境(光线、粉尘等)和测量方法等对三维形貌数据的精度都会产生影响,故在获取裂隙面三维数据后,运用自带软件CloudForm对点云数据进行降噪、去除无关点、滤除数据波纹以及补面等处理。同时,原每个裂隙面均由几十万个离散点构成,平均点距0.025 mm,数据量庞大且排列杂乱无序。为了便于分析数据,用matlab编写程序,对测量点重新删减和排序,新得到的裂隙面共计22 801个点,平均点距1 mm,如图2所示,测得的裂隙表面形貌参数见表1。
3.3裂隙分形描述与计算
粗糙裂隙表面分形维度计算方法多种。Clarke等[17]首次提出了以空间表面面积为测度,以正方形网格为测量尺度的三角形棱柱表面积法;谢和平等[18]提出投影覆盖法。这两种方法属于码尺法(driver method)范畴,计算得到的维数是相似分形维数,而不是真正意义上的几何分形维数。后来周宏伟等[19]提出计算三维表面分形维度的计盒维数法(box-counting method):立方体覆盖法和改进的立方体覆盖法。以上计算理论都是基于统计意义上的自相似性。事实上,Brown、Kulatilake等[20]学者认为岩石粗糙裂隙面符合自仿射模型特征。
对于自仿射模型,Kulatilake[21]提出以二维剖面线Z(x)变异函数值2γ(x,h)为测度,间距h为测量尺度的变异函数法(Variogram method)。
第一步:生成不同方向二维轮廓线数据。首先,将获得的裂隙表面数据划分成1 mm×1 mm网格,选取0°方向,其他方向逆时针按照θ=15°×k(k=1,2,…,11)选择,见图3。然后,计算一条方向线上高度数据Z(x,y),如对15°方向线P上坐标Q(x,y)表面高度数据ZQ对该坐标半径1 mm范围内的高度按照(6)式计算,循环获得该条轮廓线数据。再以相同的方法获得相隔10 mm的下一组轮廓线数据。最后反复循环计算获得各个方向上轮廓线数据。
Z(x,y)=ni=1Zirini=11ri(17)
式中,Zi为与Q点相距1 mm半径范围内第i个点的高度,ri为i点到Q点距离。
第二步:计算不同方向二维分形维度。对每个方向,考虑边界影响,剔除两边的二维轮廓线;然后计算各轮廓线的变异函数值2γ(x,h)
2γ(x,h)=1NNi=1[Z(xi)-Z(xi+h)] 2(18)
式中,N为轮廓线上所有间距h的数据点数。对于自仿射模型,存在如下关系
2γ(x,h)=KVh2(2-D)(19)
式中,KV为比例系数,D为二维轮廓线分形维度。对每个轮廓线计算至少7个不同间距h下的变异函数,并由式(19)拟合得到分形维度D,对一个方向下所有轮廓线的分形维度求平均,得到该方向下的分形维度D。
为了使裂隙面粗糙度各向异性特征更加直观,图4给出了5个不同裂隙面(F1~F5)分形维度的玫瑰花图。各图呈现出近似“椭圆”对称状,但分形维度随方向随机分布,裂隙面具有不规则的粗糙度各向异性结构特征。通过比较,F4裂隙面分形维度较大,其中90°方向最大,分形维度为1.60,由此可知,F4具有较大的粗糙度。
4粗糙裂隙非线性流动特性
4.1粗糙裂隙饱和渗流试验
试验中,裂隙采用上节提到的5组岩石裂隙面作为原型,用硅胶拷贝其表面的形貌,然后基于硅胶模型,用环氧树脂AB胶复制其表面形态。环氧树脂AB胶是一种液型、双组份硬性胶,固化以后形成高透明、高强度的硬性体,在试验过程中可实时观察水流流动情况。
采用自行设计的装置(见图5)对5组裂隙进行饱和渗流试验,每组裂隙进行2种流向(0°,90°)测试。测试过程记录不同流量Q下的压力差△P,试验的流量范围在0~100 mL/s之间。在上下裂隙表面匹配后,利用Kulatilake[21]提出的非接触方法确定每个裂隙开度值,F1~F5开度值分别为1.58,2.20,1.50,2.45 mm和2.10 mm。
4.2非线性流动规律
图6给出了0°方向各组裂隙流量和压力梯度的关系。当流量较小(Q<10 mL/s)时,黏滞作用占主导地位,压力梯度随着流量呈线性增加;当流量较大(Q>10 mL/s)时,惯性作用增强,流动从线性阶段过渡至非线性阶段,压力梯度将随着流量增加呈非线性递增。为了表达这种关系,结合最小二乘法,用Forchheimer公式拟合试验数据。同时拟合90°方向渗流数据,拟合结果见表2。各组裂隙的拟合精度都较高,说明Forchheimer公式能够定量描述非线性流动规律,这与Zimmerman等[3]研究结论是一致的。
为了分析流动的各向异性特征,提出了一个新的描述各向异性的参数:各向异性度▽,定义为90°向与0°向压力梯度之差与90°向压力梯度的比值。
▽=▽P90°-▽P0°▽P90°(20)
式中,▽P90°為90°向压力梯度,▽P0°为0°向压力梯度。图7给出了各向异性度随流量的变化曲线,从图可以看出:总体上,随着流量的增加,各组裂隙各向异性度在缓慢减小,但变化不明显;各组裂隙各向异性度大多在0附近“波动”,且各值有一定的差别,说明裂隙流存在各向异性特征,且与裂隙形貌和开度分布有关。
4.3非线性分形模型的验证
4.3.1系数a和b的确定
为了求解待定常数a和b,首先获取F1、F2和F3裂隙形貌数据,并根据上节方法计算分形维度;然后利用渗流试验结果(见表2),根据非线性拟合Levenberg-Marquardt法对式(16)进行拟合,得到a和b。拟合结果见图8,得到a=0.246,b=-0.964,代入式(1),(2)和(16),得
▽P=12μwe 3hQ+0.246(ehL)-0.964(1-D)ρe 3hw 2Q 2(21)
图8B与eh/L的拟合关系Fig.8Fitting relationship between B and eh/L
4.3.2非线性分形模型与其他模型的对比
为了验证模型的正确性,将非线性分形模型与渗流试验数据及Chen的双参数模型[6]对比。Chen的公式如下
▽P=12μwe 3hQ+0.0138 7ρξ0.666w 2e3.666hQ 2(22)
针对裂隙F4和F5,分别按式(21)和(22)计算压力梯度,并将结果与实验值进行比较,结果见图9。由图可知:采用非线性分形模型计算结果与实测值较为接近,相对误差大多数在20%以内,表明非线性分形模型能较好地描述裂隙介质中非线性渗流情况。而Chen的公式计算误差较大,原因在于仅仅用绝对粗糙度难以量化表面形貌对裂隙流的影响。
5分析与讨论
Forchheimer定律在裂隙介质非线性渗流中有着广泛的应用价值,但对于线性流过渡到非线性流的机制还需进一步讨论。
Zimmerman等[3]首次提出裂隙内流体流动存在线性流到非线性流的转变过程,并用非线性达西效应因子区分两种流态,认为=0.1。
=BQ 2AQ+BQ 2(23)
据此,众多学者[22]提出用临界雷诺数Re0描述这种过渡机制。对于裂隙介质,雷诺数[5]可用下式表达
Re=ρQμw(24)
将式(2)、(16)和式(23)代入式(24),并令=0.1,得到:
Rec=5.42(ehLc)-0.964(DL-1)(25)
式(25)表明,临界雷诺数与水力开度、裂隙面的分形维度及流动的方向性密切相关,水力开度越小,裂隙面越粗糙,临界雷诺数也越小,裂隙流越容易发生非线性流动。计算得到的临界雷诺数见表3,大小在30~60之间,远小于王媛等[23]认为的2300。进一步表明,裂隙隙宽分布不一,表面的粗糙所造成流动的涡流及回流效应,使得流动变得曲折,惯性阻力增加,从而导致在低的雷诺数时转变成非线性流。
6结 论
(1) 根据裂隙流具有曲折效应的特点,并用水文弯曲度和表面曲折率来描述,结合裂隙分形特征,提出了粗糙裂隙非线性渗流新公式。
(2) 运用了3D CaMega光学三维扫描系统获取了裂隙面点云数据,并采用了Kulatilake提出的自仿射模型分形维度计算方法,分析了裂隙面粗糙性的各向异性特征。
(3) 对5种不同粗糙裂隙分别从0°和90°方向进行渗流试验。试验结果表明,在高流速下,裂隙流符合Forchheimer定律,且具有各向异性特点。并对比了新模型、Chen的双参数模型和试验结果。结果表明,新模型与实验结果更接近。
(4) 根据新模型,提出了区分达西流与Forchheimer流的判据,即临界雷诺数的表达式。分析表明,临界雷诺数与水力开度、裂隙面的粗糙度及流动的方向性密切相关。
(5) 本文提出的模型没有考虑相反方向渗流各向异性特征,而这有赖于新的粗糙度参数,这将是今后研究的重点。
参考文献:
[1]许凯,雷学文,孟庆山,等.非达西渗流系数研究[J].岩石力学与工程学报,2012,31(1):164-170.
[2]Schrauf T W,Evans D D.Laboratory studies of gas flow though a single natural fracture[J].Water Resources Research,1986,22(7):1038-1050.
[3]Zimmerman R W,Al-Yaarubi A,Pain C C,et al.Nonlinear regimes of fluid flow in rock fractures[J].International Journal of Rock Mechanics and Ming Sciences,2004,41(3):163-169.
[4]Zhang Z, Nemcik J.Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures[J].Journal of Hydrology,2013(477):139-151.
[5]Zhou J Q,Hu S H,Fang S,et al.Nonlinear flow behavior at low Reynolds numbers though rough-walled fractures subjected to normal compressive loading[J].International Journal of Rock Mechanics and Ming Sciences,2015(80):202-218.
[6]Chen Y F,Zhou J Q,Hu S H,et al.Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J].Journal of Hydrology,2015(529):993-1006.
[7]金毅,鄭军领,董佳斌,等.自仿射粗糙割理中流体渗流的分形定律[J].科学通报,2015,60(21):2036-2047.
[8]Tsang Y W.The effect of tortuosity on fluid flow through a single fracture[J].Lubric Technology,1984,20(9):1209-1215.
[9]肖维民,夏才初,王伟,等.考虑曲折效应的粗糙节理渗流计算公式研究[J].岩石力学与工程学报,2011,30(12):2416-2425.
[10]谢和平.分形几何及其在岩土力学中的应用[J].岩土工程学报,1992,14(1):14-24.
[11]谢和平,周宏伟.岩体断裂面渗流特性的分形研究[J].煤炭学报,1998,23(6):585-589.
[12]Murata S,Saito T.Estimation of tortuosity of fluid flow through a single fracture[J].Journal of Canadian Petroleum Technology,2003,42(12):39-45.
[13]王刚,黄娜,蒋宇静,等.考虑分形特征的节理面渗流计算模型[J].岩石力学与工程学报,2014,33(S2):3397-3405.
[14]Ju Y,Zhang Q G,Yang Y M,et al.An experimental investigation on the mechanism of fluid flow through single rough fracture of rock[J].Science China Technological Sciences,2013(56):2070-2080.
[15]Develi K,Babadagli T.Experimental and visual analysis of single-phase flow through rough fracture replicas[J].International Journal of Rock Mechanics and Ming Sciences,2015(73):139-155.
[16]郭建春,庄园,刘超.考虑非达西效应酸蚀裂缝流场数值模拟[J].岩土力学,2015,36(11):3315-3321.
[17]Clarke K C.Computation of the fractal dimension of topographic surfaces using the triangular prism surface area method[J].Computers and Geosciences,1986,12(5):713-722.
[18]Xie H P,Wang J A.Direct fractal measurement of fractal surfaces[J].International Journal Solids and Structures,1999(36):3073-3084.
[19]周宏伟,谢和平,Kwansniewski M A.粗糙表面分维计算的立方体覆盖法[J].摩擦学学报,2000,20(6):455-459.
[20]Kulatilake P H S W,Balasingam P,Park J,Morgan R.Natural rock joint roughness quantification through fractural techniques[J].Geotechnical and Geological Engineering,2006(24):1181-1202.
[21]Kulatilake P H S W,Park J,Balasingam P,et al.R.Quantification of aperture and relations between aperture, normal stress and fluid flow for natural single rock fractures[J].Geotechnical and Geological Engineering, 2008(26):269-281.
[22]Javadi M,Sharifzadeh M,Shahriar K,et al.Crital Reynolds number for nonlinear flow through rough-walled fractures:The role of shear processes[J].Water Resources Research,2014,50(2):1789-1804.
[23]王媛,顧智刚,倪小东.光滑裂隙高流速非达西渗流运动规律的试验研究[J].岩石力学与工程学报,2010,29(7):1404-1407.
引用本文:王慧,苏永军,王凤瑞.基于分形理论的岩石裂隙非线性渗流各向异性研究[J].人民长江,2019,50(2):174-180.
Study on non-linear flow anisotropy behavior in rough rock fractures based on fractal theory
WANG Hui ,SU Yongjun ,WANG Fengrui 2
(1.Hebei University of Water Resources and Electric Engineering, Cangzhou 061001,China;2. Hebei Cangzhou Hydrology and Water Resources Survey Bureau,Cangzhou 061000, China)
Abstract: Aiming at the issue of Non-Darcy seepage flow in fracture, the seepage characteristics in different rough fractures were studied . The test speciment of fracture rock mass were obtained by splitting the integrated cubic rock mass, and the fracture surface topographies of rock mass were measured by stereotopometric scanning system. Surface roughness anisotropy was quantified by self-affine fractal dimension D using measured data. According to tortuosity effect of flow in fracture, the non-linear flow was characterized by a power law relationship of hydraulic tortuosity and fractal dimension based on Forchheimer law. Fracture seepage tests were conducted from two incidence directions (0°and 90°). The results showed that non-linear flow with anisotropy could be well described by Forchheimer law. Finally, a new formula was proposed, which can distinguish the linear flow and Forchheimer flow.
Key words:fracture; non-linear flow; fractal dimension; Forchheimer law; anisotropy; critical Reynolds number
