金沙江白格堰塞湖溃决洪水预报误差与改进
2019-10-20王敏卢金友姚仕明朱勇辉周建银
王敏 卢金友 姚仕明 朱勇辉 周建银


摘要:金沙江“11.3”白格堰塞体溃决造成下游河道数百千米内的超常规洪水过程,对其进行准确模拟是洪水预报和制定应对措施的基础。采用MIKE11和笔者开发的一维溃坝洪水模型(DBFM)对坝下洪水演进进行了对比模拟,两个模型均为求解圣维南方程组,其中MIKE11采用Abbott六点隐式差分方法,DBFM模型采用基于有限体积的HLL+MUSCL界面插值方法显式求解。结果表明:与实测数据相比,两个模型模拟结果在洪水传播时間和洪峰衰减上表现出显著差异。随后分析了河道基流、动量方程惯性、河道糙率、河道地形等因素对洪水模拟误差的影响,论证了采用滚动预报方法来提高洪水预报精度的可行性。最后对山区河流堰塞湖溃决洪水模拟的难点和要求提出了展望。
关键词:堰塞湖;洪水演进;数值模拟;滚动预报;金沙江
中图法分类号:P33
文献标志码:A
DOI:l0.16232/j.cnki.1001-4179.2019.03.007
文章编号:1001-4179(2019)03-0034-06
2018年10月11日和11月3日,西藏江达县波罗乡白格村川藏交界的金沙江上游河道右岸同一位置两次发生山体滑坡形成堰塞湖。其中“11·3”堰塞坝是在“10·11”堰塞湖溃决残余坝体基础上形成的,其坝高较“10·11”堰塞坝还高约30m。为降低蓄洪量、减小洪水风险,采取了人工挖槽泄流的措施。11月12日,泄流槽进水,11月13日13:45,坝前水位达到最高点2956.40m。
为提前预估堰塞湖下游金沙江沿岸洪水风险,给居民转移、工程处置水库调度等应急决策提供科学依据,堰塞湖形成后,在水利部长江水利委员会组织下,长江科学院相关技术人员采用成熟的商业软件MIKE11开展了洪水演进计算。堰塞湖溃决后,又根据沿程各站实测流量过程,开展滚动预报计算。应急决策过程中,因时间仓促,资料不足,模拟结果难免存在一定的误差。
溃坝洪水的模拟比常规水流模拟困难,其原因在于:①山区河道地形比降大、起伏剧烈;②流量在时空上变化极为剧烈,存在干湿变化,间断特征显著。此外,山区河流地形水文资料缺少、强非恒定非均匀流的阻力仍未明晰等原因,均可能造成溃坝洪水模拟的误差。由于堰塞湖不太常发生且实测资料较少,模拟实际堰塞湖洪水的成果不多。2008年唐家山堰塞湖发生后,众多学者进行了堰塞湖溃决洪水演进的模拟。刘帆采用具有人工黏性的修正MacCormack数值格式计算了溃坝洪水的一维演进张细兵、朱勇辉、黄明海也计算了唐家山堰塞湖的溃决洪水及其演进,采用的是MIKE11的Abbott六点隐格式和传统的四点偏心格式求解圣维南方程组。
模拟一维水流运动的圣维南方程组是一个双曲型方程组。为准确模拟间断,差分格式必须满足守恒性。其中,有限体积方法天然满足守恒性,适合用来构建溃坝洪水模拟的模型。大部分溃坝模型隐含矩形河道假设,不适应于山区河道。张大伟建立了采用Z和Q为求解变量的一维有限体积溃坝模型,采用HLL格式的近似黎曼解求解界面通量并采用MUSCL方法对界面两侧物理量进行了重构,宋利祥以此为基础建立了河网模型,郑川东进一步将水面梯度项,放入对流项中,以更好地满足动量守恒。这些模型理论上适合应用于实际山区河道的溃坝洪水,但是尚待实践检验。向小华采用特征线方法求解了以A和Q为变量的非守恒形式的圣维南方程组,构建了一维河网模型。以守恒变量A、Q为基本变量,求解守恒型方程,更符合方程守恒性的本质,也是准确捕捉间断的要求。
本文采用MIKE11模型和笔者建立的基于有限体积法的一维溃坝洪水模型(DBFM),对金沙江“11·3”白格堰塞湖溃决洪水演进过程进行对比计算;通过模拟不同的参数和工况,分析模型、地形、水流状况等因素对洪水模拟预报误差的影响;论证了滚动预报对提高模拟预报精度的效果。
1 模型介绍
1.1 MIKE11模型
MIKE11模型求解一维圣维南方程组,其形式如下:
公式
式中,t,x为时间和一维坐标;A,z,,R,Q分别为过水断面面积、水位、水力半径以及断面流量;Qi为单位长度内的旁侧入流量;β为动量方程惯性项修正因子。MIKE11模型默认惯性项修正因子取值为
公式
MIKE11模型采用Abbott六点隐格式进行离散,离散所得的三对角方程采用追赶法进行求解。
1.2 一维溃坝洪水模型
为模拟山区复杂条件下可能存在间断的溃坝洪水,笔者构建了一维溃坝洪水模型(DBFM)。模型采用有限体积法离散圣维南方程组。采用HLL格式的近似Riemann解对界面进行插值。界面通量的计算为
公式
式中,V为求解变量,S为传播流速(此处为流速),F(V)为界面通量,下标L、R代表界面的左、右。为提高界面插值的精度,对界面两侧的变量,采用MUSCL方法对界面两侧变量进行数值重构。以第i个控制体的右界面(i+1/2)为例,界面两侧的通量为
公式
式中,公式是限制器。本次研究所用模型采用VanLeer限制器:
公式
参考Ying对水位梯度源项采用顺风差分以保证稳定性。有限体积模型在出入口各需两个条件。Zhang在模型出入口,除了,上游给流量、下游给水位之外,还各补充了一个水位流量关系。该模型考虑到出口水位无法给定,除给定入口流量和出口水位流量关系之外,入口补充条件为根据连续方程离散得到的新时刻水位和流量的关系,出口补充条件为流量沿程梯度为零。
2 实测洪水过程模拟对比
堰塞湖模拟计算时,以实际溃口流量过程为入口条件。溃口流量过程由坝前水位过程与堰塞湖水位-库容曲线推算。河道糙率取0.05,模拟范围从溃口至其下游河道600km。模拟所用河道地形由DEM地形数据提取。沿程主要站点的断面形态如图1所示。可见,DEM无法获取水下地形高程,故计算采用的断面地形有一定的概化,可能与实际河槽有一定的区别,这将不可避免地带来模拟误差。
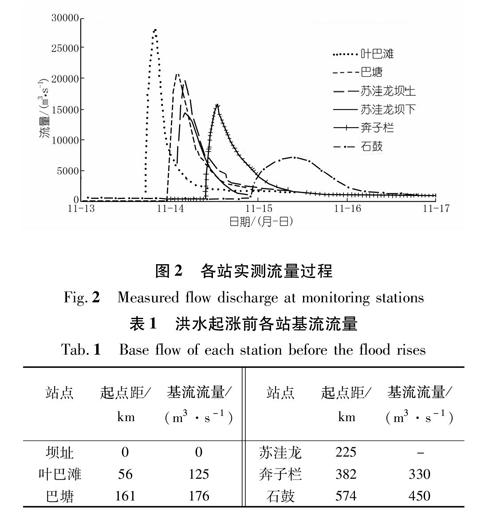
图2是各站实测流量过程。需要指出的是,由于洪水陡涨陡落,现场水位的测量较为困难,有时不得不借助临时测站,而本次奔子栏以上各站的洪峰流量超过了有记录历史最大洪水,这使得按照水位流量关系推算的流量也存在一定的误差,加上非恒定流的水位流量关系本身也存在争议,因此实测流量和水位本身也可能存在一定的误差。
实际洪水并非发生在干河道上,河道本身有一定的基流。根据各站洪水起涨前的流量资料,可以得到沿程的河道基流情況。其中有些来自支流入汇,因缺少支流流量资料,本次统一按照区间均匀入汇考虑。各站基流流量如表1所示。
计算和实测各站洪峰过程过程对比如图3所示。由图可见:与实测相比,苏洼龙以。上,DBFM模型比MIKE11模型符合性更好,而苏洼龙以下则相反。DBFM模型洪峰衰减较快,洪峰传播时间符合较好,而MIKE11模型计算洪峰衰减较慢,但是洪峰传播速度较快。预报时若能结合两者的模拟结果,可以提高预报的精度。从苏洼龙坝上和坝下的实测流量过程差异可见,苏洼龙电站拦蓄了部分洪水,显著改变了洪水过程。由于模型并未考虑苏洼龙的拦蓄作用,因此,苏洼龙以下模拟结果与实测的符合是一种“巧合”。
3 误差分析
3.1 河道基流的影响
为分析河道基流的影响,模型模拟的条件除了溃坝下游初始河床为干河床,其他与上一节一致。图4是溃口下游2个测站的实测流量过程与计算流量过程的对比。与图3对比可见,干河床条件下洪水传播速度变慢,洪峰流量减小。
3.2 动量方程惯性项的作用
模型计算表明,此次溃坝洪水整个过程均为缓流,且Fr数绝大多数在0.5以下。但是,溃坝洪水本身可能出现急流,因此,此处仍对惯性项的作用予以分析讨论。MIKE11模型采用的是Abbott六点隐格式,具有很强的适应能力,但是,对于急流仍有局限。为了克服急流模拟的困难,引入了LPI(Local Particial Intia)因子。该因子在缓流时不起作用。DBFM模型可以正常模拟紊流情况,不需要对动量方程惯性项加以限制。
图5对比了惯性项正常计算和归零时各站的洪水过程。
由图5可见,惯性项归零后,洪水过程更为“尖瘦”,但作用有限。由于动量方程惯性项对流量过程实际起着扩散坦化的作用,在溃坝洪水模拟中,若出现急流,由于惯性项被抑制,MIKE11模型可能锐化洪水过程、增大洪峰流量。
3.3 河道糙率的影响
河道糙率对洪水模拟的精度也有一定的影响。糙率越大,阻力越大,同流量下水位越高槽蓄量越大、流速越小。图6对比了糙率取0.05和0.06两种情况下叶巴滩和巴塘站洪水过程。可见,糙率增大后,洪水过程被推迟、洪峰流量减小。
3.4 其他影响因素分析
前面分析表明,河道基流、糙率、动量方程惯性项的处理均会对溃坝洪水模拟有一定的影响。因缺少足够的资料,苏洼龙围堰拦蓄洪水过程未能在模拟中考虑,这是造成苏洼龙及其下游洪水模拟误差的重要原因。从基流的作用可见,支流入汇对洪水演进也有影响,特别是支流来流量较大的情况。
本次洪水模拟误差最大的影响因素是地形误差。由于缺少水下地形资料,河槽变得比实际宽浅得多。一方面,同样水深情况下,过水面积要大得多,这将导致洪水下泄时流量过程的坦化;另一方面,缺少水下地形相当于抬高了河底,由于沿程并非均匀抬高,则可能增大河床纵比降,加快洪水运动。其综合效果,与具体河道情况有关。
4 滚动预报
由于本次溃坝洪水下游传播距离长达600km以上,长距离计算必然导致误差的累积。溃口的流量过程本身也存在不小的误差,尤其是在峰值流量上。本次溃坝洪水模拟预报时,由于苏洼龙围堰的拦蓄未能在模拟中加以考虑,苏洼龙下游洪水过程的模拟预测更难以实现。在此情况下,利用溃决过程中沿程多个测站的实测洪水资料,不断校正模型参数,进行滚动模拟,就可以成为减小模拟误差、提高预报精度的有效手段。此处仍采用DBFM模型,以奔子栏水文站为入口起算下游洪水演进过程。图7是石鼓断面计算与实测流量过程的对比。可见,计算结果在峰值和相位上,均与实测符合较好,比图3从溃口开始推算的石鼓流量过程大为改善。
5 结语
本文采用两种基于不同求解方法的数值模型进行对比计算,分析了河道基流、糙率、动量方程惯性项、河道地形等因素对模拟误差的影响,论证了采用滚动预报的方法可以提高模拟精度。
(1) 山区河流河床大比降、高起伏,溃坝洪水过程强非恒定,且可能出现急流或干湿间断,这些复杂条件对数值模型的模拟能力提出了挑战。
(2) 河道基流、糙率、动量方程惯性项、河道地形均会对溃坝洪水模拟有一定的影响,其中地形的影响相对较大。基于溃决过程中实时监测数据的滚动预报方法可提高洪水模拟和预报的精度。
(3) 实际预报中,综合采用多个模型对比预测,能够提高洪水预报的精度和把握,更好地为应急决策提供支撑。
(4) 山区河流资料缺乏,使得溃坝洪水模拟预报存在一定程度的不确定性。快速、精确地获得山区河流河道地形数据,是山区河流溃坝洪水模拟和预报迫切需要解决的问题。
参考文献:
[1]刘帆.一维溃坝模拟及四川堰塞湖应急计算[D].北京:清华大学,2008.
[2]王光谦,付旭东,李铁建,等.汶川地震灾区堰塞湖应急处置中的计算分析[C]//中国科协防灾减灾论坛,2008.
[3]张细兵,卢金友,范北林,等.唐家山堰塞湖溃坝洪水演进及下泄过程复演[J].人民长江,2008,39(22):76-78.
[4]朱勇辉,范北林,卢金友,等.唐家山堰塞湖溃坝洪水分析及泄流冲刷模拟[J].人民长江,2008,39(22):79-82.
[5]黄明海,金峰,杨文俊.不同河道状况下的堰塞坝溃坝洪水特性研究[J].人民长江,2008,39(22):66-68,82.
[6]Michel-Dansac V,Berthon C,Clain S,et al. A well-balanced
scheme for the shallow-water equations with topography or Manning friction[J]. Journal of Computational Physics,2017(335):115-154.
[7]Valiani A,Caleffi V. Momentum balance in the shallow water equations on bottom discontinuities[J]. Advances in Water Resources,2017(100):1-13.
[8]LeFloch P C,Thanh M D. A Godunov-type method for the shallow
water equations with discontinuous topography in the resonant regime[J].Jourmal of Computational Physics,2011,230(20):7631-7660.
[9]張大伟,程晓陶,黄金池,等.复杂明渠水流运动的高适用性数学模型[J].水利学报,2010(5):531-536.
[10]宋利祥,李清清,胡晓张,等.基于有限体积法的河网水动力并行计算模型研究[J].长江科学院院报,2018(14):1-7.
[11]郑川东,白凤朋,杨中华.求解守恒形式的圣维南方程中处理不规则断面的一种改进方法[J].水电能源科学,2017(12):95-99,103.
[12]向小华,吴晓玲,牛帅,等.通量差分裂方法在一维河网模型中的应用[J].水科学进展,2013(6):894-900.
[13]DHI. MIKE 1D Reference manual]EB/OL].2017.
[14]Ying X,Khan A A, WangS S Y.Upwind Conservative Scheme for the Saint Venant Equations[J]. Journal of Hydraulic Engineering,2004,130(10):977-987.
[15]Zhang s,Duan J G. 1D finite volume model of unsteady flow over mobile bed[J]. Jourmal of Hydrology,2011,405(1):57-68.
引用本文:王敏,卢金友,姚仕明,朱勇辉,周建银.金沙江白格堰塞湖溃决洪水预报误差与改进[J].人民长江,2019,50(3):34-39.
Study on dam break flood forecast error and improvement for Baige barrier lake on Jinsha River
WANG Min,LU Jinyou,YAO Shiming,ZHU Yongwei,ZHOU Jianyin
(Changjiang River Scientific Research Institute,Changjiang Water Resource Commission,Wuhan 430010,China)
Abstract:The broken of "11.3" Baige barrier lake on Jinsha River resulted in the ultra-normal flood in hundreds of kilometers of the downstream. Accurate simulation of the flood is the basis of the flood forecast and the development of the response measures. The flood routing law in the downstream of the dam was simulated by MIKE11 and a one-dimensional dam break flood model developed by the author. The two models both solve the Saint-Venant equations,while the MIKE1 1 uses the Abbott six-point implicit difference method and the DBFM model uses a finite volume of the HLL + MUSCL interface interpolation method. The simulation results showed that the two models show differences in the flood propagation and the peak attenuation comparing with the measured data. Then,the influence of the factors such as the channel base flow,the momentum equation inertia,the channel roughness and the channel terrain on the simulation error of the flood were further analyzed,and the feasibility of using rolling forecast method to improve the flood forecast accuracy was demonstrated. In the end,the difficulties and requirements of the dam break flood simulation of the barrier lake in the mountainous area were put forward.
Key words:barrier lake;flood routing;numerical simulation;rolling forecast;Jinsha River
