基于改良CW算法求解带时间窗的烘焙食品的配送问题

卜尚勤 师梽源 刘宇航 王海玲

摘要：本文运用一种改良节约法求解带时间窗的烘焙食品运输过程中所产生的VRPTW问题。首先通过引入分割配送的思想计算出分割配送的反应值H，然后根据反应值的大小决定优先分割顺序，最后结果提高了配送里程和装载率，效果良好。

关键词：时间窗；节约算法；配送问题

中图分类号：TP301.6 文献标识码：B 文章编号：1672-9129（2019）04-0007-05

Abstract：This paper solved the problem of VRPTW in the process of baking food transportation with time window based on an improved saving method. Firstly， the response value H of segmented distribution is calculated by introducing the idea of segmented distribution. Then the priority division order is determined according to the size of the store's response value . Finally， the result improves the delivery mileage and loading ratio， and the effect is good.

Keywords：Time window；CW algorithm； VRPTW

引言

物流行业迅速发展的今天，像烘焙食品这样需要严格上架时间的行业，需要更高效，更合理，更节省成本的配送方案，带时间窗约束的路径规划问题由此提出。车辆路径规划不仅满足严格的上架时间，还为食品厂商降低了运输成本与人工费用。解决带有时间窗的车辆路径规划问题时，需要分析的因素有很多，国内学者曾玉霞在CW算法的基础上进行改进，得到了提高配送车辆载重率改进算法，并验证了改进算法可行性和优越性[1]。王芳在节约算法的改进中加入了分割配送的想法，更接近于实际问题的考虑，得到了车辆路径问题的满意解[2]。邵俊岗，郑芳瑜等人针对基于分割配送思想的改进节约算法中可能存在的交叉路径导致增加运输里程数的情况，对连接点选择问题进行优化，得到优于CW算法的改进算法[3]。崔宏志，龚加安对带时间窗的单类型车辆路径问题进行深入研究，加入邻域搜索的思想，为避免路径交叉，提出了改进后的CW算法[4]。

本文通过改良的CW算法，结合分割配送的思想，解决一种是带时间约束的硬时窗下的车辆路径问题。

1 车辆调度问题概述

车辆调度问题最早是由Dantzig和Ramser于1959年提出来的[5]，并且许多现实生活中的的实际问题的理论都可以归结于这一问题。由于应用前景广阔，所以成为运筹学与组合优化领域的研究热点[6]。

车辆运输调度问题一般定义为：对一系列装货点和卸货点规划适当的行车路线，使车辆有序地通过它们，满足一定的约束条件，如时间窗口约束、车辆容量限制、车辆行驶里程限制、司机最大工作时间限制等，达到一定的目标如：车辆行驶路程最短、运输费用最少、使用车辆数最少、服务质量最高等[7]。

其中，车辆调度问题中最常见的问题之一就是VRP（Vehicle Routing Problem， 车辆路由问题），它是用来确定一些有容量限制的且同时必须满足一系列的约束的车辆在配送过程中的最优路径 [8]。VRP的解就是设计出一个或多个满足这样要求的最短配送路线，可以包括貨品体积约束、车辆需要进行保养和维护的里程数约束、车辆行驶路程约束、时间窗口约束等。

2 模型建立

以内蒙古呼和浩特市意林食品作为原型，挑选了位于动车站、学校聚集区、市中心、景区以及随机两个居民区的六家门店作为配送对象。以江淮帅铃4.2m冷藏车（额定载重1495kg）作为运输工具，每辆冷藏车运输成本约每公里0.5元，以百度地图所规划的最短路线作为运输路径，以百度糯米店铺流量作为店铺需求量指标进行合理推测，人为规定时间窗范围进行规划。

为了使模型更直观，工厂用0表示，门店用1-6示，即1：火车站店；2：昭乌达路店；3：

新华大街店；4：五塔寺店；5：竹园店；6：海西路店。具体位置如图1所示。

工厂与门店间、门店与门店间的里程表如表1所示。

根据表1门店间里程表求解配送最短路，运用Dijkstra算法求解最短路步骤如表2所示。

根据表2可知，门店间里程即为门店间的最短路。门店需求量如表3所示。

2.1 模型的假设

为了使模型不会受到各种现实因素的影响，作出了如下假设：

（1）车辆运输不受天气或拥堵及红绿灯等不受控因素的影响；

（2）门店之间的最短距离有且只有一条，不考虑城市单行线的情况；

（3）配送的烘焙食品可以混送；

（4）工厂拥有足够配送的食品和配送车辆；

（5）配送车辆的速度恒定；

（6）车辆运费不随货物质量的变化而变化。

2.2 经典CW算法介绍

CW算法基本原理：依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。

具体求解步骤如下：当工厂为多个门店配送食品时，首先计算出各个门店间的节约里程，按照节约里程从大到小的顺序依次将门店加入到行车路线中。同时判断该门店需求量是否超过了当前车辆的额定载重，若超过则剔除该门店，结束本路径规划；若不超过则继续安排剩余节约里程中最大的一条路线，以此类推，直到所有门店被安排到行车路线中。

2.3 经典CW算法模型求解

根据表1可计算出门店间的节约值如门店1、2间的节约值如式1所示。

以式1依次得到所有门店的节约值并降序排列，结果如表4所示。

根据表4开始构造行车路线，由表3的门店需求量是否超过车辆载重，依次加入到配送路径中。由表3可知，节约值最大的路线为（4，6），连接（4，6）后得到的行车路线为0-4-6，这时的门店需求量为230+746=976<1495，未超过车辆额定载重；再由降序表加入路线（2，4）后得到的行车路线为0-2-4-6，这时的门店需求量为976+318=1294<1495；在由降序表加入路线（3，2）后得到行车路线0-3-2-4-6，这时门店的需求量为1294+436=1730>1495，这时门店需求量超过了车辆额定载重，因此这条路径不能加入行车路线；再根据降序表分别依次加入（2，5）、（1，6）等路线会发现路线加入后的门店需求量均超过了车辆的额定载重，因此这些路径都不能再加入到行车路线中。此时就规划出了第一条行车路线0-2-4-6，这条行车路线的节约值为24.5+23.2=47.7km。

这时门店2、4、6都加入到了行车路线中，根据表3选出除了包含门店2、4、6的节约值最大路线（3，5），连接门店3、5后得到行车路线0-3-5，此时的门店需求量为436+738=1174<1495，未超过车辆额定载重；再由降序表加入路径（1，3）后得到行车路线0-1-3-5，这时的门店需求量为1174+382=1556> 1495，这时门店需求量超过了车辆额定载重，因此这条路线不能再加入到行车路线中。此时就规划出了第二条行车路线0-3-5-0，这条行车路线的节约值为14.2。此时只有门店1没有加入行车路线，因此门店1只能单独配送，得到第三条行车路线0-1-0。

综上所述，意林工厂向其6个门店配送的路线一共有3条，分别是：

R1：0-2-4-6-0

R2：0-3-5-0

R3：0-1-0

运用经典CW算法求解VRP问题结果是：工厂需要2辆冷藏车进行配送，节约的里程为

（4.1+12.0+11.0+15.0+9.8+14.9）*2-（（12.0+3.8+5.4+14.9）+（11+6.6+9.8） +（4.1+4.1））=61.9km；如不对行车路线进行规划，原运输成本为（4.1+12.0+11.0+15.0 +9.8+14.9）*2*0.5=66.8元，进行路线规划后，现在的运输成本为（12.0+3.8+5.4+14.9）+ +（11+6.6+9.8） +（4.1+4.1））*0.5=35.85.9 元，节约成本为66.8-35.85=30.95元。

3 改良CW算法求解VRPTW模型

VRPTW模型在经典CW算法的基礎上增加车辆的行车速度40km/h，门店允许配送的时间范围是9：00-9：30，卸货时间根据即时门店需求量进行合理推断，车辆装载率需要高于90%。

3.1 改良CW算法求解步骤

在经典CW算法的基础上通过改良求解思路结合分割配送的思想后，改良CW 算法的具体执行步骤如下：

步骤1：将门店解初始化。为每个门店都只分配一辆车进行单独配送，使之成为只有一个门店的行车路线。

步骤2：计算门店间的节约里程，并按照降序排列构成降序表。

步骤3：回路合并。从降序表中找出节约值最大的路径合并加入到行车路线中，这时也需要考虑卸货时间为路径规划所带来的影响，之后判断此时门店需求量是否超过车辆额定载重，若超过额定载重则考虑分割配送；若不超过，则在节约里程表中去除该路径，更新降序表后进行下一步。

步骤4：计算车辆从出发点到下一个门店的时间及门店卸货时间t，若t超出硬时间窗范围，剔除该客户的路线合并；若没超出，计算此时车辆载重率，若车辆载重率小于等于90%，返回上一步。若载重率超过90%，这条路线规划完毕，开始规划下一条行车路线

步骤5：考虑分割配送方案，首先根据层次分析法计算VRPTW问题中两个约束条件里程c和行程时间t的权重a和b，再计算剩余客户分割配送反应值H，按照H从大到小的顺序决定分割配送哪个客户需求，将客户需求分为车辆剩余重量和其他，为剩余重量配送后，判断时间t是否超出硬时间窗范围，若没超出，更新门店需求量，得到新路线，进行下一条路线规划；若超出，取消本次分割配送。

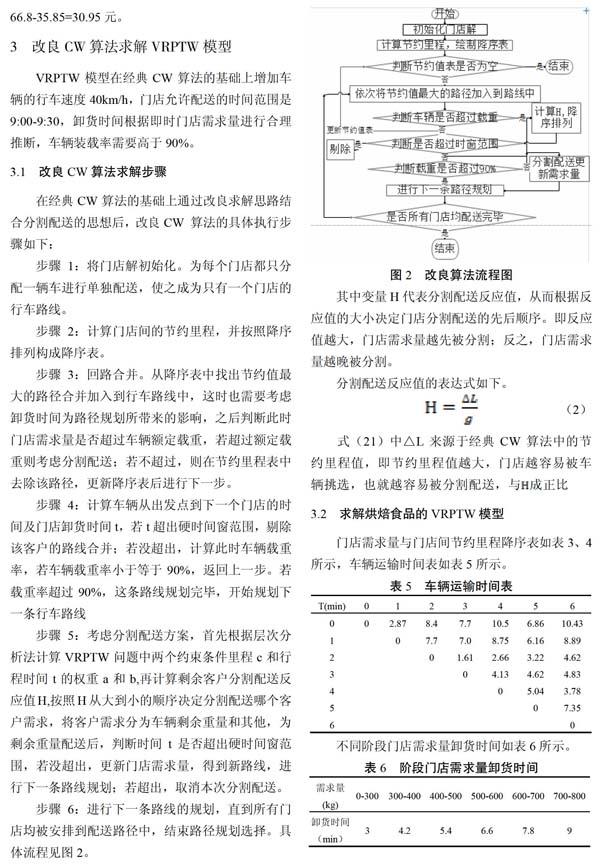
步骤6：进行下一条路线的规划，直到所有门店均被安排到配送路径中，结束路径规划选择。具体流程见图2。

其中变量H代表分割配送反应值，从而根据反应值的大小决定门店分割配送的先后顺序。即反应值越大，门店需求量越先被分割；反之，门店需求量越晚被分割。

分割配送反应值的表达式如下。

3.2 求解烘焙食品的VRPTW模型

门店需求量与门店间节约里程降序表如表3、4所示，车辆运输时间表如表5所示。

运用改良CW算法求解烘焙食品运输过程中的VRPTW问题步骤如下：

初始化解，工厂为每个门店分配一辆冷藏车进行单独运输，运输成本为66.8元。

在表3中找到最大节约路径（4，6），连接门店4、6后得到路线0-4-6，此时门店需求量为230+746=976<1495，未超过车辆额定载重；在判断车辆的运输时间，冷藏车均在9：00从工厂出发，有时间窗条件9：00-9：30可知，允许配送的时间为30min，卸货时间3min，总时长10.5+3.78+3=17.28min<30min，车辆装载率为65.3%<90%；接着在路线中加入路径（2，4）后得到路线0-2-4-6，此时门店需求量为976+318=1294<1495，未超过车辆额定载重，卸货时间为4.2+3=7.2min，总时长为8.4+2.66+3.78+7.2=22.04min<30min，车辆装载率为86.6%；接着在路线中加入路径（2，3）后得到路线0-3-2-4-6，此时门店需求量为1294+436=1730>1495，超过车辆额定载重，若考虑将门店3分割配送，考虑门店3在满足额定载重的情况下最长卸货时间为3min，此时总运输时间为7.7+1.61+2.66+3.78+3+4.2+3=25.95min<30min，门店3这时满足分割配送的条件，运输里程与运输时间的权重分别为0.75和0.25，将门店3到门店2的节约值、运输里程与运输时间带入（2）中，此时门店3的反应值H3=9.80，这时将门店3的需求量分割为235和201，更新门店3需求量为235，此时车辆满载，第一条路径规划结束，得到行车路线0-3-2-4-6-0。

继续从剩余未被规划完全的门店路径节约值表中找到最大节约路径（3，5），连接3、5得到路径0-3-5，此时门店需求量为235+738=973<1495，这时没有超重，车辆载重率为65.0%<90%，卸貨时间为3min，总运输时间为7.7+4.62+3=15.32min；结合卸货时间及节约值表，接着在路径中加入（1，3），得到路径0-1-3-5，门店需求量为382+973=1355<1495，车辆载重率为90.6%>90%，卸货时间为4.2min，总运输时间为2.87+7+4.62+4.2+3=21.69min。第二条路径规划结束，得到行车路线0-1-3-5-0

综上所述，意林工厂向其6个门店配送的路线一共有2条，分别是：

R1：0-3-2-4-6-0

R2：0-1-3-5-0

运用改良CW算法求解VRPTW问题结果是：工厂需要2辆冷藏车进行配送，节约的里程为65.7km，如不对行车路线进行规划，原运输成本为（4.1+12.0+11.0+15.0+9.8+14.9）*2*0.5=66.8元，进行路线规划后，现在的运输成本为（（11+2.3+3.8+5.4+14.9）+（4.1+10+6.6+9.8））×0.5=33.95元，节约成本为66.8-33.95=32.85元。

4 结论

从运输里程来看，经典CW算法的运输里程为65.7km，改良CW算法计算出的运输里程为61.9km，改良的算法比改良前节约了3.8km。相应的，经典CW算法的运输费用为35.85元，改良CW算法计算出的运输费用为33.95元，节约了1.9元。从车辆数目来看，原算法下工厂使用冷藏车3辆，改良后的算法中工厂只需要冷藏车2辆，较原算法节约了1辆。从装载率比较，原算法下的车辆装载率分别只有86%、78%和26%，改良算法下车辆装载率分别为100%和90.6%，均超过90%，显然在装载率上改良CW算法较经典CW算法有了较大提高。

参考文献：

[1] 曾玉霞.C-W节约算法的改进研究[A].北京：中国职协2015年度优秀科研成果获奖论文集（中册）.2015：6-13.

[2] 王芳.基于节约算法和改进节约算法的配送路线优化[J].商.2015，51：194.

[3] 邵俊岗，郑芳瑜.车辆路径问题的连接点选择节约算法[J].佳木斯：佳木斯大学学报（自然科学版）.2015， 2：13-18.

[4] 崔宏志，龚加安.带时间窗车辆路径问题的改进节约算法[J].纯粹数学与应用数学.2011，5：256-273.

[5] 邓宇佑.求解医院运输部门运输中心个数最佳化之研究（D）.成功大学工业管理研究所硕士论文，1991年.

[6] 刘洋. 一种应用于物料配送路径选择的改进CW算法.吉林大学，2017年

[7] 潘立军.带时间窗车辆路径问题及其算法研究[J].长沙：中南大学.2012

[8] 张建同，冯子炎.求解车辆路径问题的改进CW节约算法[A].北京：第十届中国不确定系统年会、第十四届中国青年信息与管理学者大会论文集.2012，7：75-83.