曲面上布朗运动的数值计算

周文杰 冮铁强

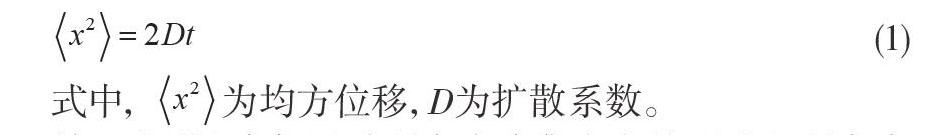
摘   要：本文将以二维曲面为研究对象，建立正则曲面上布朗运动轨迹与测地线之间的联系，通过测地线的相关理论，实现曲面上的布朗运动数值计算。通过对布朗运动均方位移的计算验证爱因斯坦关系。

关键词：布朗运动  二维曲面  测地线  数值计算

中图分类号：O552                                  文献标识码：A                        文章编号：1674-098X（2019）05（b）-0014-02

Abstract： In this paper， the two-dimensional manifold surface is taken as the research object， and the relationship between the Brownian motion trajectory and the geodesic line on the regular surface is established. The theory of the geodesic is used to simulate the Brownian motion on the manifold. The Einstein relationship is verified by the calculation of the mean square displacement of the Brownian motion on the manifold

Key Words： Brownian motion; Two-dimensional manifold surface; Geodesic; Numerical Simulation

愛因斯坦于1905年发表论文[1]，对布朗运动[2]的机理进行了定量的描述，得到了著名的爱因斯坦关系：

式中，为均方位移，D为扩散系数。

关于流形上布朗运动研究大多集中在从理论上研究布朗运动的性质[3]，本文将以二维曲面为研究对象，提出利用测地线的方法实现二维曲面上布朗运动的数值计算。

1  测地线与布朗运动

在微分几何[4]中，存在关于测地线一个重要的定理：

定理1：曲面S上的一条曲线是测地线，当且仅当它或者是一条直线，或者它的主法向量处处是曲面S的法向量。

假设质量为m的布朗粒子在曲面S上运动，运动轨迹为r（t），粒子仅受曲面法向约束力力F（t）的作用。由牛顿第二定律可得：

由式（2）可知的方向沿着曲面S的法方向，因此可知粒子运动轨迹的主法向量为曲面S的法向量，结合定理1可得布朗粒子的运动轨迹为曲面S上的测地线。

2  曲面上布朗运动的数值模拟

曲面上测地线所满足方程为：

当u1、u2为正则参数系时，还满足：

式中θ为测地曲线与u1-曲线的夹角。

曲面S上的布朗运动随机方向的定义，以对夹角θ的随机来生成。下图1为利用测地线方法实现布朗粒子在曲面S上随机运动800步的轨迹图。

3  均方位移计算

曲面上对均方位移的计算采用计算两点间的测地距离。下图2为计算得到的均方位移图，可以看到，布朗运动均方位移与时间之间满足爱因斯坦关系。

4  结论

（1）曲面表面的布朗运动轨迹为曲面上的测地线，利用测地线的理论实现了二维曲面上布朗运动的数值模拟;

（2）二维曲面表面的布朗运动的均方位移依然满足爱因斯坦关系，即均方位移与时间的线性关系。

参考文献

[1] Einstein A. ?ber die von der molekularkinetischen Theorie der W?rme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen[J]. Annalen der physik， 1905， 322（8）：549-560.

[2] 郝柏林.布朗运动理论一百年[J].物理，2011，40（1）：1-7.

[3] Castro-Villarreal P. Brownian motion meets Riemann curvature[J]. Journal of Statistical Mechanics： Theory and Experiment， 2010， 2010（8）：P08006.

[4] 陈维桓.微分几何[M].北京大学出版社，2017.