基于综合赋权法的港口物流竞争力评价
2019-10-19
(1.山东科技大学 交通学院,山东 青岛 266590;2.海洋石油工程(青岛)有限公司,山东 青岛 266520)
随着世界各国对港口资源的大规模开发利用以及我国在港口物流方面的快速发展,港口物流竞争力评价对港口发展发挥着日益重要的作用。港口物流竞争力是港口在腹地区域经济和基础设施建设基础上,通过提高港口运作效率和资源利用率,达到在物流方面优于市场其他港口的能力。由于港口物流受设备、场地及天气等因素的影响,因此物流竞争力评价是一个多指标综合评价的过程。港口物流竞争力的确定需要采用科学、合理、多样化的评价方法,建立数学模型进行优劣排序,从而求解多指标评价问题。
在解决多指标评价问题时,需要先确定各评价指标的权重。权重的确定方法主要分为两类:一是主观赋权法,其权值通常根据专家经验或各指标对评价的重要程度进行主观赋值,如层次分析法、专家调查法和二项系数法等[1-4];二是客观赋权法,是根据客观数据与各评价指标之间的关系,通过建立数学模型进行赋值的,如熵值法、变异系数法、主成分分析法和加权平方和法等[5-8]。两种赋权方法各有优缺点:主观赋权法基于决策者在现实中对指标的重视程度及决策经验,能够将复杂的问题简单化,且其决策结果较符合实际,但是带有一定的依赖性和主观臆断性;客观赋权法将指标权数与指标变量值相联系,能够体现数据本身的性质,有较强的数学理论依据,且不依赖于评价者的主观判断,但是不能体现出各指标在实际中的重要程度。而基于层次分析法与信息熵的综合赋权法能够结合两种评价方式的优点,并缩小两者权重的偏差,在主观评价与客观评价间寻求权重的一致性。吴梦烟等[9]基于灰色局势决策和组合赋权法对再生水的综合发展能力进行评价。在应用组合赋权时通过层次分析法和熵值法分别计算指标权重,引入距离函数对两种方法所得的权重进行组合赋权。李素平[10]利用有序加权算子,综合多位专家对指标打分求得的不同指标权重进行组合赋权,建立广义偏差最小的物流产业集群竞争力评价模型。
本研究采用综合赋权法,建立评价模型对各港口的物流竞争力进行评价,并评价结果分别与交通运输部和社会的港口评价进行对比,验证其合理性。本文所提出的方法可以合理评价港口物流竞争力,并为港口发展提供参考。
1 数据标准化处理
在多指标评价过程中,正向指标值越大则评价越优,而逆向指标值越小则评价越优,因此两者不能够以同样的标准进行评价。为统一不同指标量纲对评价计算的影响,使得正向指标和逆向指标具有可比性,需要将评价矩阵中的数据进行标准化处理。设多指标综合评价问题中有m个评价指标,指标集记为C={C1,C2,…,Cm},有n个评价对象,记为P={P1,P2,…,Pn},则评价对象Pj对指标Ci的属性值为xij(i=1,2,…,m;j=1,2,…,n),评价矩阵可表示为X=(xij)m×n。定义
(1)
则评价矩阵标准化后可表示为R=(rij)m×n。
2 指标权重的确定
2.1 层次分析法的权重确定
采用层次分析法确定主观权重时,需要先将各评价指标划分层次级,并将同一级指标的重要性进行两两对比,根据九标度法[11]将各指标的重要度定量化,构造判断矩阵Dij。九标度法判定及其含义如表1所示。
由于判断矩阵是根据评价者对指标重要度的主观排序,存在一定误差,因此需要进行一致性检验来修改判断矩阵。判断矩阵Dij的特征方程为:
D·W=λmax·W。
(2)
式中,λmax表示判断矩阵Dij的最大特征根(存在且唯一),W表示最大特征根λmax所对应的特征向量。对特征向量W归一化处理后可得主观权重向量W1=(ω1,ω2,…,ωm)Τ。
其次对判断矩阵进行一致性检验。一致性检验指标可表示为:
(3)
当CI为0,即最大特征根λmax=m时,该判断矩阵具有完全一致性;当CI大于0时,随着CI的增大,判断矩阵的一致性逐渐减弱,此时需要根据随机一致性比率CR判定矩阵是否具有满意的一致性。

表1 九标度法判定及其含义Tab.1 Definition and meaning of the nine-scale method
(4)
式(4)中,RI为平均随机一致性指标,不同阶数对应不同的RI值,其值详见表2。当CR值小于0.1时,可认为判断矩阵Dij的一致性较为满意;否则需要修改判断矩阵,直至得到满意结果。

表2 平均随机一致性指标数值表Tab.2 Numerical table of mean random consistency index
2.2 信息熵的权重确定
熵是对不确定信息的度量,用来描述信源的不确定度。熵值越小,权重越大,说明指标数据信息的无序度越小,即不确定度越低,信息值越有效,该指标越重要。在有n个评价对象,m个评价指标的评价矩阵中,第i个评价指标的信息熵值可表示为[12]:
(5)

根据评价指标的熵值可以确定其权重。指标Ci的客观权重为:
(6)
因此各指标的客观权重向量为W2=(μ1,μ2,…,μm)Τ。
2.3 综合权重及评价值的确定
综合赋权法[13]是一种结合层次分析法的主观权重及信息熵的客观权重的方法,通过对层次分析法和熵权法求得的指标权值分别乘以一个调整系数得到新的指标权值,并根据博弈论的思想构建两个新指标权值与原指标权值间差值总和最小的矩阵函数,从而求得各指标的综合权重。综合赋权法的优点是兼顾评价者主观偏好及数据的客观属性,能够在两种评价方式所得权重间寻找一致性,缩小主、客观权重的偏差。基于k个权重向量的综合权重集合W的确定方法如下:
(7)
式中αi表示不同评价方法所得权重的线性组合系数,对αi进行优化可得到使综合权重与各评价方法权重离差最小的最佳权向量W。通过构建如下交叉规划模型可以求得该综合权向量W:
(8)
由矩阵的微分性质可知,对矩阵函数进行一阶求导构造出线性方程组可求得矩阵离差最小时的解,当式(9)最优时需满足:
(9)
可表示为如下线性方程组:
(10)
将式(10)中的αi求解出来并代入式(8)即可得到综合权重向量W。评价对象Pj的评价值可由线性加权法[14]计算:
(11)
3 模型应用
以我国部分港口为例[15],通过7项评价指标对港口的物流竞争能力进行评价,从而选取物流竞争力较强的港口。各港口评价指标及数据如表3所示,其中港口物流吞吐能力系数由港口货物吞吐量及港口集装箱货物吞吐量确定,假定两者对吞吐能力的贡献相同,根据加权平均法[16]对两者均赋1/2的权值,因此港口物流吞吐能力系数可表示为:

表3 港口物流竞争力评价指标及数据Tab.3 Evaluation index and data of port logistics competitiveness
3.1 层次模型的建立
在港口物流竞争力评价中,将模型划分为目标层G、准则层C以及方案层P三个层次,其中目标层为交互式多指标综合评价排序;准则层包括港区装卸机械设备数C1,港口万吨级泊位数C2,港口陆域面积C3,港口物流吞吐能力系数C4,港口覆盖的航线数C5,港口机械设备自动化相对水平与作业能力C6和自然状况对港口物流的影响程度C7;方案层为5个港口,分别为P1大连,P2宁波,P3厦门,P4深圳和P5湛江。
3.2 主观权重的确定
根据评价者对各评价指标的主观偏好及重视程度,可得判断矩阵
根据式(3)对以上判断矩阵Dij求最大特征值,得λmax=7.035 2。最大特征值对应的特征向量作归一化处理后可得主观权重向量为:
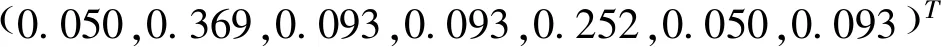
其次进行一致性检验。由式(4)、(5)得一致性检验指标CI=0.005 9,随机一致性比率CR=0.004 5<0.1,说明能够满足一致性,即判断矩阵符合要求。
则评价值向量f为:
f=(0.670,0.896,0.654,0.772,0.301)。
3.3 客观熵权的确定
根据基数标度法将定性指标C6和C7进行定量化,得5个港口对指标C6和C7的属性值分别为5、6、8、4、2和4、3、6、6、6。由表3中数据建立评价矩阵X=(xij)m×n。

在评价指标中,指标C1~C6为正向指标,C7为逆向指标,因此需要将评价矩阵X标准化为R=(rij)m×n,由式(1),(2)计算得标准化矩阵R为:

矩阵R归一化后得P=(pij)m×n:

由此可计算各港口中评价指标的信息熵值E为:

则指标Ci的客观熵权
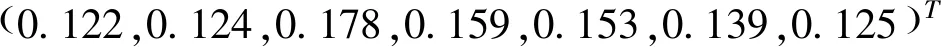
则评价值向量
f=(0.596,0.854,0.649,0.748,0.301)。
3.4 综合权重及排序
将求得的主观与客观权重分别代入式(11)中可得W1、W2所对应的归一化系数分别为α1=0.915 6,α2=0.084 4。将W1、W2和α1、α2代入式(8),得结合主、客观的综合权重

各港口的评价值向量
f=(0.664,0.893,0.653,0.770,0.301)
3.5 货物和集装箱吞吐量影响因子的讨论
在建立基于综合赋权的港口物流竞争力评价模型时,假定货物和集装箱吞吐量对港口物流吞吐能力系数的贡献相同,即两者对港口物流吞吐能力系数的影响因子均为0.5。为验证这一假定的合理性,分别对货物和集装箱吞吐量采用多种影响因子,并计算和比较不同影响因子所对应的客观评价值向量和综合评价值向量。计算和对比结果如表4所示。

表4 不同货物和集装箱吞吐量影响因子对应的计算结果Tab.4 Calculation results of corresponding impact factors to different cargo and container throughput
根据表4可知,当货物和集装箱吞吐量对港口物流吞吐能力系数的影响因子分别采用(0.5;0.5),(0.4;0.6),(0.6;0.4),(0.3;0.7)和(0.7;0.3)时,各港口物流竞争力的客观评价值和综合评价值排序均相同,即客观评价值由高到低依次为宁波、深圳、厦门、大连和湛江,综合评价值由高到低依次为宁波、深圳、大连、厦门和湛江。由此说明货物和集装箱吞吐量对港口物流吞吐能力系数的贡献差异对物流竞争力评价值的影响较小,可以忽略;对货物和集装箱吞吐量分别采用(0.5;0.5)的影响因子是合理的,可以在此基础上进行评价值的计算和比较。
3.6 结果分析
根据综合赋权法得到的结果对各港口的物流竞争力进行排序与评价,通过与层次分析法和信息熵的结果进行对比分析,得到不同模型在多指标评价中的区别。计算结果如表5所示。

表5 不同方法计算结果比较Tab.5 Comparison of calculation results by different methods
由表5可知:
1)层次分析法与综合赋权法求得的指标权重较为接近,且前5个较大权重的指标排序相同,依次为C2,C5,C3,C4,C7(层次分析法中C3,C4,C7的权重并列第3)。
2)熵权法求得7个指标的权重分别为0.122、0.124、0.178、0.159、0.153、0.139和0.125,在数值上较小且较为接近,说明在该案例中各港口对应的评价指标数据较为客观,信息有效度较高。三种方法求得的港口评价值均表明港口2(宁波港)的物流竞争力最强,港口4(深圳港)位居第二,港口5(湛江港)最弱。
3)层次分析法和综合赋权法所得排序结果相同,且两种方法对于港口1(大连港)、港口3(厦门港)的相对排序与熵权法有所不同。主要原因在于指标权重的差异,其中层次分析法和综合赋权法中指标2(港口万吨级泊位数)的排序均为第一,而熵权法中指标2偏后,同时指标2的数据中P1>P3,表明层次分析法与综合赋权法中指标2港口所能容纳万吨级船舶停泊的泊位数对于物流竞争力评价有重要影响,故港口1(大连港)优于港口3(厦门港)。
4)综合赋权法得到的港口评价值整体介于层次分析法与熵权法之间,对港口物流竞争力的排序较一致,说明综合赋权结合了对指标的主观重视度与数据的客观属性,结果合理可靠。
4 物流竞争力提升建议
通过对港口的7个评价指标进行分析,在综合赋权法中,港口万吨级泊位数和港口覆盖航线数的指标权值分别为0.348和0.244,占据了评价模型整体权重的主要部分,说明以上两个指标对于提高港口物流竞争力发挥着重要的作用,因此各港口在发展过程中应着重扩大万吨级泊位数和覆盖的航线数,为产业运营提高良好的硬件设施基础。在评价指标中,港口陆域面积、物流吞吐能力系数和自然状况的权值较大,分别为0.1、0.099和0.096,建议适当扩大港口建设规模和产业规模,选址或建设选择U形或V形的深水区以规避风浪,减小自然状况对港区的影响。而指标权重较小的装卸机械设备数和机械设备自动化水平与作业能力由于对物流竞争力的影响较小,可在港口的基础设施建设和产业规模达到较高水平后,作为提升物流竞争力的补充。
对于模型中的五个港口,建议最具物流竞争力的宁波港和深圳港在机械设备方面进行改善,以提高产业运作效率,促进规模的进一步扩大;对于物流竞争力较强的大连和厦门港,两者在港区规模上稍有优势,但大连港位于我国的北部,易受温度、雾霾和海冰等自然因素的影响,而厦门港位于我国较南端,易受风、雨、雷和雾等自然因素的影响,因此大连港和厦门港需要加强自然天气的预警和防御,尽量减小自然状况对产业运作的影响;对于物流竞争力相对较弱的湛江港,由于港区陆域面积小,航线覆盖条数少,因此建议扩大港口建设规模,为物流吞吐等产业运作奠定良好的基础。
5 结论
采用主观与客观赋权相结合的方法建立了多指标评价模型,在满足对指标主观偏好的同时兼顾其客观属性。通过层次分析法和信息论中的熵值理论,分别确定了各指标的主客观权值。根据综合赋权法结合主客观权值,由线性加权法得出各评价对象的综合评价值。将该模型应用于港口物流竞争力的评价中,并与仅采用层次分析法或熵权法的结果进行比较分析。三种方法所得各港口的评价值较为接近,相对误差大部分位于3%以内。通过对其排序可知三种方法中港口2(宁波港)均列物流竞争力第一位,港口4(深圳港)均列第二位,港口1(大连港)和3(厦门港)位列第三或第四位,港口5(湛江港)均列末位,说明评价结果基本一致。根据交通运输部公布的2018年1—9月份港口货物和集装箱吞吐量数据,在模型的五个港口中,宁波港货物及集装箱吞吐量均列第一,深圳港的集装箱吞吐量较大位列第二,而湛江港虽货物吞吐量较大但集装箱吞吐量极低。结合各港口规模和经济效益进行排名,社会上普遍认为以上港口中宁波港和深圳港较有优势,具有更大的发展潜力,而湛江由于在基础及产业方面受限,与其他港口存在一定的差距,大连及厦门两个港口各有优势,但均介于深圳及湛江之间。将综合赋权法所得港口物流竞争力排名与现实中各港口的排名和评价进行比较,表明本研究结果符合实际情况,验证了模型评价结果的合理性。综合以上分析,基于综合赋权法建立的评价模型是一种可靠有效的方法,可以为港口物流竞争力的评价与择优提供依据。
