基于改进的遗传算法优化BP神经网络的车险欺诈识别模型

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

汽车保险是我国财产保险中的第一大险种。随着车险投保数量以及金额的不断提高，车险理赔量也随之大幅增加，汽车保险诈骗案件数目也不断上升。保险欺诈的存在，从长远来看影响着保险公司的定价策略和社会经济效益，甚至严重威胁到了我国保险业的发展[1]。

近年来国内外学者在保险欺诈识别研究上引入了多种人工智能技术。叶明华[2]以中国机动车保险为例，提出利用BP神经网络与logit回归相结合的保险欺诈检测模型，利用logit回归分析选出显著性指标，最后通过检测结果分析，与logit回归相结合的BP神经网络模型识别的准确率要高于单独使用BP神经网络识别的结果。汤俊和莫依雯[3]利用支持向量机和Apriori算法等数据挖掘技术，提出车险反欺诈的检测系统模型，利用Apriori挖掘到的规则对支持向量机判断出来的可疑案例进行再检验,提高了检验的准确性。闫春等[4]提出基于随机森林和蚁群算法的汽车保险欺诈识别模型，该模型对汽车保险索赔数据和挖掘欺诈规则进行更有效的分类和预测，具有更好的准确性和鲁棒性。ubelj等[5]提出一种既考虑实体内在属性也考虑实体之间的关系的一种迭代评估算法(iterative evaluation algorithm,IAA)，通过结果分析，该系统能够有效检测到汽车保险欺诈行为。Yaqi等[6]提出一种基于主成分分析的潜在近邻随机森林法，用于汽车保险欺诈的识别，最后通过实证说明提出的方法具有较好的准确率以及较强的鲁棒性[6]。Yan等[7]将最近邻剪枝规则的改进孤立点检测方法应用于汽车保险欺诈，实验结果表明，改进的汽车保险欺诈识别算法具有时间复杂度低、识别率高等优点。

传统的BP神经网络具有初始权值随机，导致学习效率低、收敛速度慢，并且容易形成局部极小值而得不到全局最优的缺点。遗传算法因其良好的寻优能力，被许多学者[8-11]用于优化BP神经网络的初始权值，以实现对BP神经网络的优化。以上文献在试验中都证明了用遗传算法优化的BP神经网络其预测效果优于单独使用BP神经网络的预测效果。基于上述研究，提出一种改进的自适应遗传算法与BP神经网络算法相结合的识别算法，利用该算法进行汽车保险欺诈的识别。在考虑到BP神经网络具有很强的预测能力，同时遗传算法具有很好的寻优能力的基础上，该模型将遗传算法和BP神经网络算法有机结合。文中将已有的车险欺诈数据指标先进行分类量化，然后将量化的数据进行主成分分析，选出车险欺诈的主成分指标，作为BP神经网络的输入。文中改进的自适应遗传算法考虑了种群适应度的多种集中分散程度，并且非线性地自适应调节遗传算法的交叉概率与变异概率。为了提高遗传算法的收敛效率以及寻优能力，不仅在最优保存策略基础上加入排序选择策略，而且提出了保留亲本的策略。通过改进的自适应遗传算法对BP神经网络的初始权值进行优化，实现对汽车保险欺诈的识别分析。

1 改进的遗传算法优化BP神经网络

1.1 BP神经网络

BP神经网络具有很强的非线性映射能力，是一种多层前馈神经网络，其学习规则是最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

1.2 改进的自适应遗传算法

1.2.1 改进的自适应遗传算法

传统遗传算法(genetic algorithm)是一种通过模拟自然进化过程搜索最优解的方法，但是在处理一些较为复杂的优化问题时，容易陷入到一些局部的极值点。本研究提出了一种改进的自适应遗传算法(new adaptive genetic algorithm，NAGA)，既考虑了种群适应度的多种集中分散程度，又非线性地自适应调节遗传算法的交叉概率与变异概率；为了提高遗传算法的收敛效率以及寻优能力，不仅在最优保存策略基础上加入排序选择策略，而且提出了保留亲本的策略。

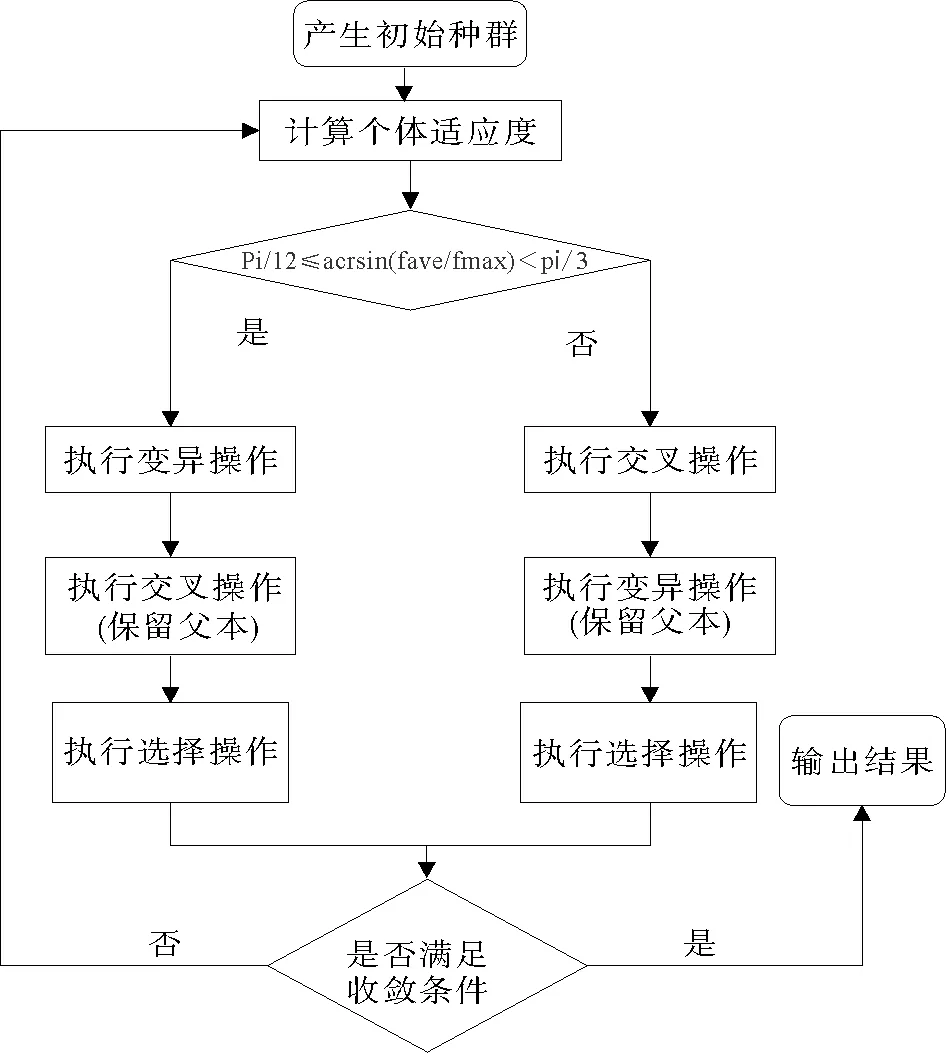
图1 改进的自适应遗传算法的运算流程图Fig.1 Flowchart of the improved adaptive genetic algorithm

改进的自适应遗传算法过程为：

1)编码初始群体(L)，设置各个参数；

2)设置适应度函数，计算各个体的适应度值，保留最大适应度个体；

3)判断是否满足收敛条件，如果满足收敛条件，则输出结果，否则进入步骤4)；

4)判断π/12≤arcsin(fave/fmax)<π/3 是否成立，如果成立，先执行变异操作，然后进行交叉操作(此操作保留父代)；反之先执行交叉操作。最后执行选择操作；

5)判断选择操作的结果是否满足收敛条件，若满足则输出结果，否则回到步骤2)。

求解流程图如图1所示。

之所以用π/12≤arcsin(fave/fmax)<π/3来判断是否先进行交叉，因为在种群中容易出现除最高适应度之外其余适应度都集中很小的情况，此时的fave/fmax<1/2，如果根据杨从锐[12]IAGA算法思想则将此种情况列为种群处于分散状态，将先进行交叉操作，但是此种情况下种群集中在较小适应度下，种群差异度较小，种群不丰富，如果先进行交叉会使得种群进化速度加慢，导致收敛慢或不易收敛，正是考虑到此种情况，本文改变条件公式，使得改进算法考虑更加全面。

1.2.2 改进选择算子

传统的遗传算法利用轮盘赌的方法来进行个体的选择，这种方法虽然优良亲本的选择概率较高，但容易造成优良亲本被选中的情况，即“退化”现象，为避免出现该现象，增加了排序选择策略和最优保存策略，即利用排序选择策略将个体按适应度从大到小进行排序，淘汰掉适应度小的排列位于后1/4的个体，直接保留排列位于适应度大的前1/4个体做为下一代的父本，将中间1/2个体保留继续操作[13]，以有效地把握种群进化的方向。

然后，将保留下来的1/2种群计算出个体的选择概率进行轮盘赌选择：

(1)

(2)

式中，qmax、qmin分别是最初定义的最佳个体和最差个体的选择概率，M是最大迭代次数。

利用公式(1)、(2)，从保留下来的1/2个体中根据轮盘赌选择策略选出一半的个体，将这一半的个体与第一步中复制下来的前1/4个体组成一个个体数量为L/2(L为初始种群)的父代种群。为了保持种群数目恒定，在进行选择概率之前的最后一次操作保留父代；为了防止了中间过程中产生或者错过更优良的个体，又采用了最优保存策略[13]，即把新产生种群中的最高适应度与前一代的最高适应度比较，如果高于子代的最高适应度，就随机淘汰掉子代中的一个个体，把前一代中最高适应度个体加入到新一代中产生一个新的种群，此保存策略保证了前一代的优良个体不会被交叉变异等遗传操作破坏。

1.2.3 自适应调节Pc与Pm的值

传统的遗传算法采用固定的交叉概率与变异概率，但是随着后期优良个体的增加，如果不改变变异概率与交叉概率的大小，将会破坏掉优良的个体。为了更充分地使交叉概率Pc和变异概率Pm在遗传操作中发挥作用，本文在杨从锐[12]的IAGA的基础上提出交叉概率Pc和变异概率Pm的值的自适应公式(3)、(4)。

(3)

(4)

其中，k1、k2分别取1.0、0.05，k3和k4分别取0.02和2。之所以用 arcsin(fave/fmax)作为判断条件是因为随着fave的变化，arcsin(fave/fmax)的变化会更快，这样便能更好地判断种群适应度之间的集中分散程度。用是否大于等于π/6来判断是因为sin(π/6)=1/2，当arcsin(fave/fmax)≥π/6时，fave/fmax≥1/2，说明适应度平均值接近适应度最大值，即种群适应度接近最大适应度集中分布。

1.3 NAGA-BP算法

本节提出的方法是将经过改进的遗传算法用于优化BP神经网络的权值，以达到解决BP神经网络初始权值随机所带来的收敛速度慢、求解精准度不高等问题。

NAGA-BP算法过程为：

1)数据预处理，确定BP网络拓扑结构，编码初始群体(L)，设置各个参数；

2)令测试样本误差作为目标函数，设置遗传算法适应度函数；

3)进行遗传操作，计算各个体的适应度值；

4)判断是否满足收敛条件，如果满足，则进入BP神经网络操作，否则进入步骤5)；

5)判断π/12≤arcsin(fave/fmax)<π/3 是否成立，如果成立，先执行变异操作，然后进行交叉操作(此操作保留父代)；反之先执行交叉操作。最后进行选择操作；

6)将选择操作的结果进行判断是否满足收敛条件，若收敛则输出结果，否则回到步骤2)。

具体流程图如图2所示。

2 NAGA-BP算法在车险欺诈识别中的应用

为了验证所提出的算法在车险欺诈识别中的有效性，选取某保险公司车险历史索赔的数据为例进行欺诈识别分析，数据来源于文献[4]。

2.1 汽车保险欺诈测度相关指标选取

在进行车险欺诈预测之前，需要对数据进行重要指标的选取，将选出的指标作为BP神经网络的输入向量。根据已知的投保人信息，选取部分信息作为汽车保险欺诈研究的指标。再根据相关研究，初步选取15个对车险欺诈存在影响的指标因子：车辆渠道来源、被保险车辆使用性质、被保险车辆所属性质、驾驶人性别、有无事故认定书、出险记录、定损照片张数、历史索赔次数、勘察类型、配件上报修理个数、所标修理厂类型额等。各变量类型说明如表1所示。

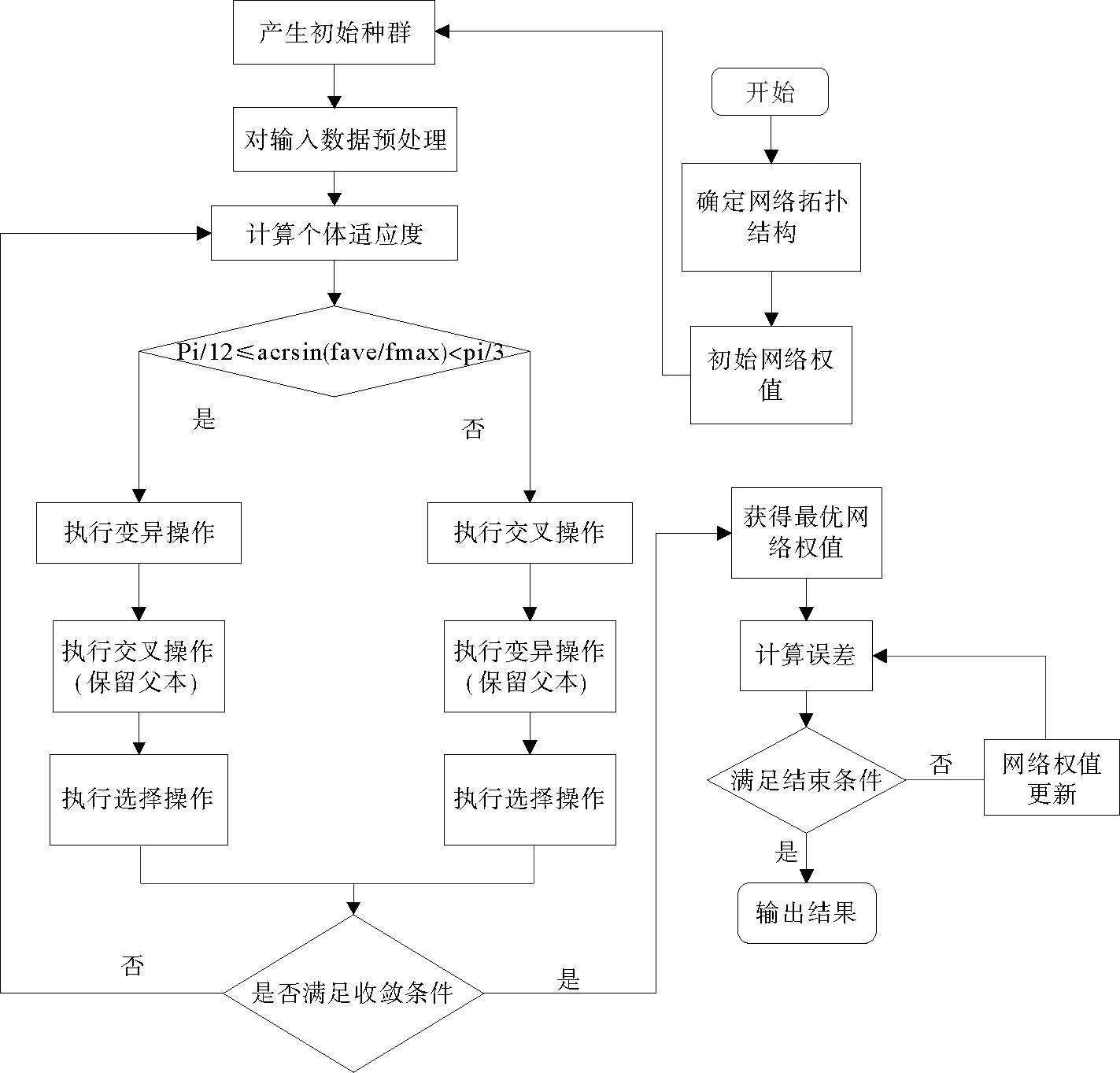
图2 改进自适应遗传算法优化BP神经网络的流程图Fig.2 Flowchart of the BP neural network optimization by improved adaptive genetic algorithm

表1 数据集指标描述Tab.1 Data set index description

从表 1 的汽车保险索赔数据变量指标描述中，可以看出存在非数值型的分类变量以及布尔型变量，需要将这些数据进行分层并进行量化处理。分层结果如表 2 所示。

如果选取所有的指标进行分析，多个指标之间可能存在相关性，并会影响模型的识别效率，增加数据处理的复杂程度。所以接下来需要对这15个欺诈识别指标进行降维处理。

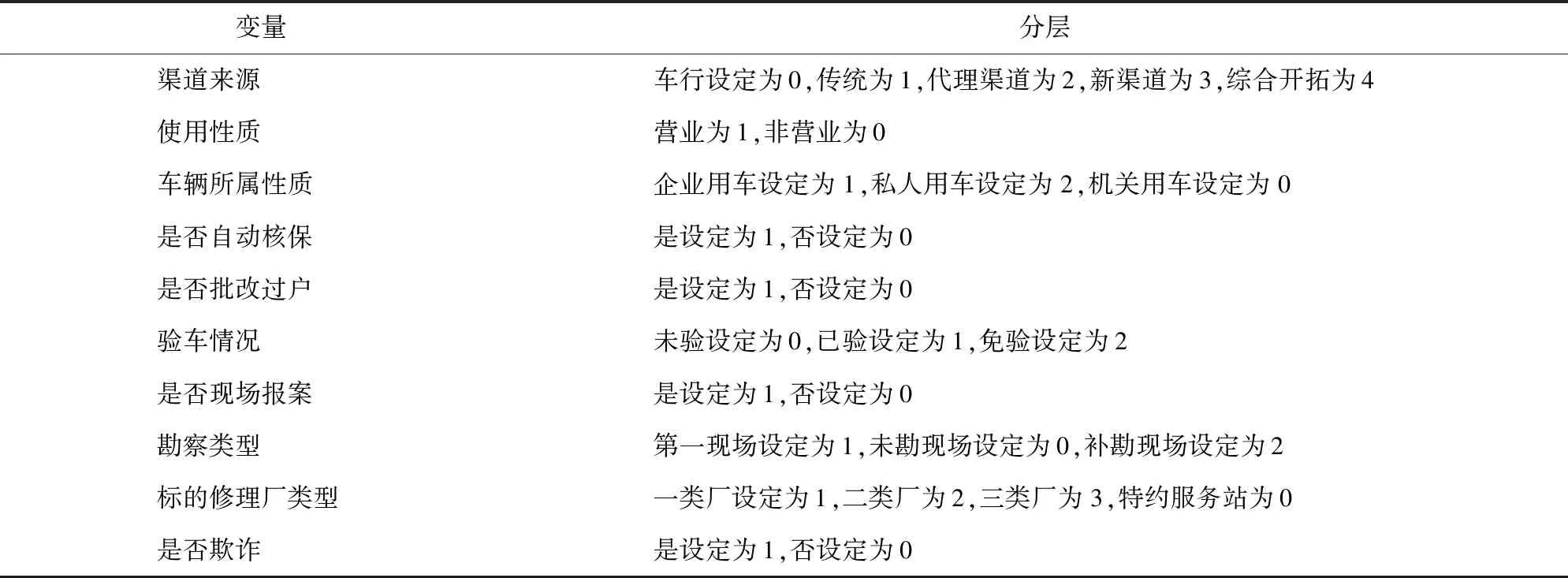
表2 分类变量的分层Tab.2 Stratification of classified variables

主成分分析法是一种多元的统计方法，能够对多维度的特征矩阵进行降维处理，减小数据的复杂程度，并且降维后的数据能够保留原始数据的主要信息。表3为将15个欺诈识别数据进行主成分分析的结果，第一主成分贡献率为16.637%，第二主成分贡献率为12.752%，前9个主成分累计贡献率达80.167%，因此提取前9个主成分作为模型的输入变量。

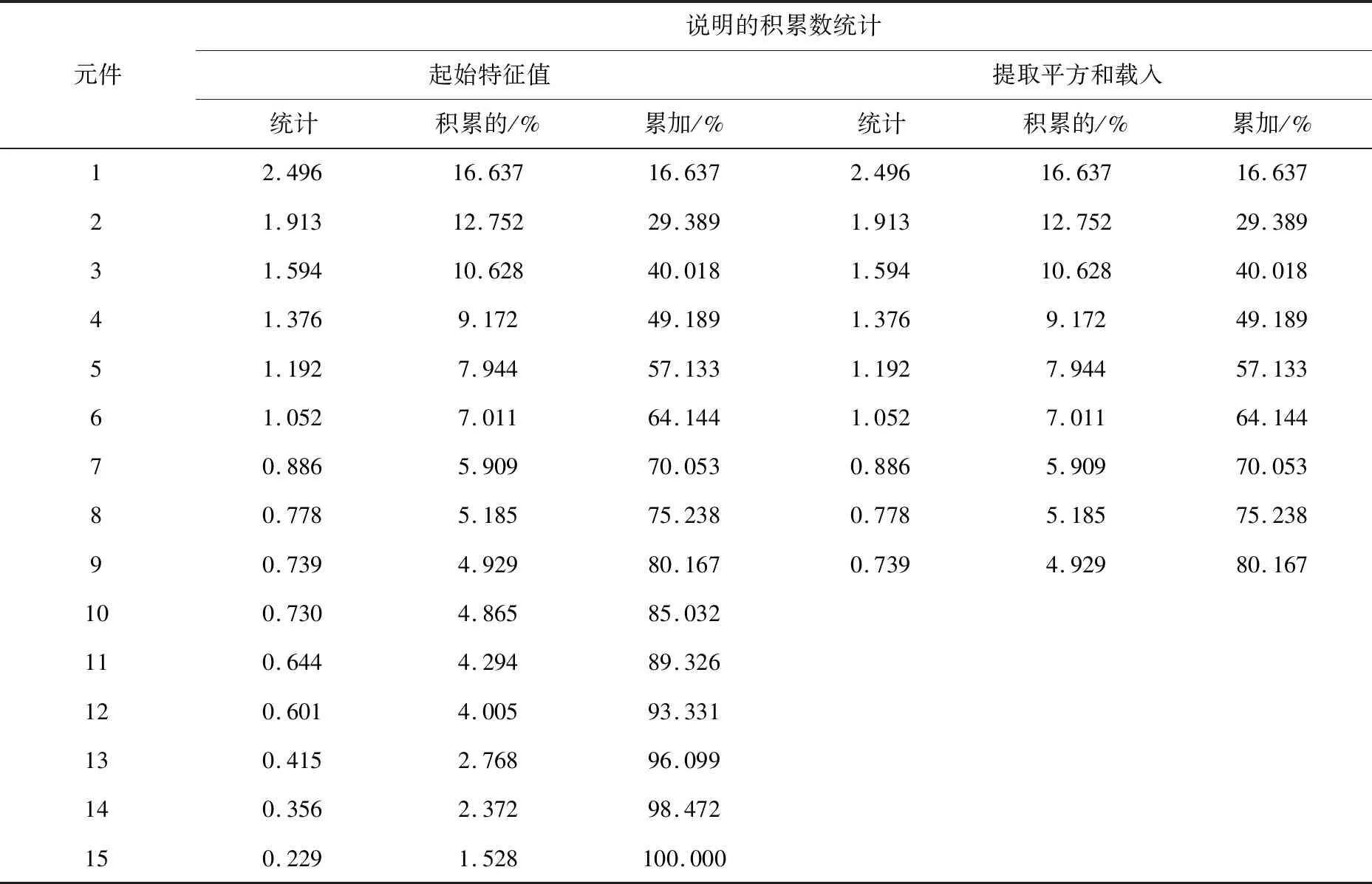
表3 主成分分析结果Tab.3 Principal component analysis results

图3 误差变化图Fig.3 Error variation diagram

2.2 欺诈识别结果

将选出的9个主成分作为神经网络的输入，即BP神经网络输入层具有9个节点，根据公式p=2m+1确定隐含层节点数为19。将是否欺诈作为输出，令保险欺诈索赔输出为1，诚信索赔输出为0，因此输出层节点数为1。将79例车险欺诈样本分为两部分，其中70例为训练样本，剩余9例为检验样本；采用训练样本来训练BP神经网络、GA算法优化的BP神经网络、IAGA算法优化的BP神经网络，以及本研究的NAGA算法优化的BP神经网络。将检验样本输入训练后的模型，获得欺诈识别的预测结果，再将各个结果与原始数据对比，以此评价各模型对于车险欺诈预测的良好程度。

从图3中可以看出，改进的NAGA算法无论是在最优解的取值上，还是在收敛速度上，都明显高于GA和IAGA算法。自适应的调节遗传算法的交叉率和变异率，能够提高遗传算法的寻优能力，而利用排序选择和最优保存策略相结合的选择策略，有利于加快遗传算法的收敛能力，因此NAGA遗传算法在收敛速度与精准度等方面都有较大的进步。

本文利用平均绝对百分比误差(MAPE)与预测方差(MSE)来评价实验的误差，其中

(5)

(6)

式中：N为测试样本个数，本文取N=9，yi和xi分别为第i个样本的实际值与测试值。

图4 各遗传算法优化BP神经网络对比图Fig.4 Comparative diagram of optimized BP neural networks by genetic algorithm

图4(a)、4(b)为预测样本输出的原始值分布(Standard data)和三种遗传算法优化BP神经网络预测(NAGA-BP、IAGA-BP、GA-BP)的样本输出值和单独使用BP神经网络系测的样本输出值(BP)。图4(a)中*线代表保险公司判定的是否欺诈的实际值，图4(b)中O线表示NAGA-BP神经网络给出的预测值，当预测值逼近 1代表预测该索赔为欺诈索赔；当实际值逼近 0代表预测该索赔为诚实索赔。此时按照 9个影响因子训练的 BP神经网络，从预测结果可以看出欺诈预测和诚实索赔预测除了样本1、3、6、8、9逼近真实值外，样本2、7的判定处于模棱两可的状态，并且第4个样本的判断结果与真实值相反，所以单纯的BP神经网络对于车险欺诈的识别不理想。利用9个影响因子来训练改进的NAGA算法优化BP神经网络，从预测结果中可以看出，预测的9个样本都逼近真实值，所以NAGA-BP模型预测出的车险欺诈情况较为理想。

表4 算法预测误差对比Tab.4 Comparison of prediction errors

通过表4的各误差对比可以看出，未经过优化的BP神经网络的预测误差方差为0.130 2，经过GA-ZAGA优化的网络输出误差分别为0.049、0.020 9，而经过本文改进的遗传算法NAGA优化的网络输出误差方差0.010 7，预测值更加接近原始数据，进一步说明本文算法改善了BP网络容易陷入局部极小值和收敛速度慢的问题。

3 结束语

随着我国保险的快速发展，车险欺诈现象也逐渐蔓延，急需提出一种有效识别车险欺诈的方法来挖掘潜在的欺诈客户，根据客户的索赔资料判断其是否欺诈，以便提前采取相应措施阻止欺诈产生。

本研究通过主成分分析，将某保险公司的欺诈索赔数据进行指标的提炼，将提炼后的指标用于模型欺诈预测的变量，以此验证NAGA- BP算法的识别欺诈能力。提出的NAGA算法自适应调节遗传算法的交叉概率与变异概率，有效地提高了遗传算法的寻优能力。利用NAGA优化BP神经网络的预测算法，考虑到神经网络的预测能力，以及遗传算法具有的搜索和优化的特点，将遗传算法与神经网络相结合，以此来克服神经网络收敛速度慢和易陷入局部极小值等缺点。在最后的实证分析中，用改进的遗传算法与IAGA和GA算法比较，NAGA算法在收敛速度与精准度等方面都有较大的进步，然后将这3种遗传算法分别优化BP神经网络进行保险欺诈数据预测，结果表明改进的NAGA-BP算法得到的车险欺诈预测数据更加接近原始数据。