基于GA与SA的社区检测优化算法研究

王妍 吴克晴 刘松华

摘 要：社区结构是网络最重要的属性之一，近年来社区检测受到极大关注，出现了很多社区发现算法。模块度是衡量社区划分好坏的重要指标，但是其分辨率却有一定局限性。将模块度中加入一个可调参数，根据社区结构调整参数更适合于需求不同的社区检测。随着网络规模的扩大，社区发现算法既要有较高的准确性，又要有很低的时间复杂性。提出一种发现算法GASA，該算法将遗传变异与模拟退火相结合，既有遗传算法的全局搜索能力，又有模拟退火算法的局部搜索能力。该算法用于社区检测优势明显，检测到的社区更接近真实社区。

关键词：模块度;遗传变异算法;模拟退火算法;社区检测

DOI：10. 11907/rjdk. 191002 开放科学（资源服务）标识码（OSID）：

中图分类号：TP312文献标识码：A 文章编号：1672-7800（2019）009-0077-04

A Community Detection Optimization Algorithm Based on GA and SA

WANG Yan，WU Ke-qing， LIU Song-hua

（College of Science， Jiangxi University of Science and Technology， Ganzhou 341000， China）

Abstract： Community structure is one of the most important attributes in the network. In recent years， community detection has attracted great attention， and many community discovery algorithms have emerged. Modularity is an important index to measure the quality of community division， but its resolution has some limitations. This paper adds an adjustable parameter to modularity， which can be adjusted according to community structure， and is more suitable for community detection with different needs. With the enlargement of network scale， community discovery algorithm not only needs to satisfy higher accuracy， but also reduces the computing time of the algorithm. So a discovery algorithm GASA is proposed， which combines genetic mutation with simulated annealing. It has both global search ability of genetic algorithm and local search ability of simulated annealing algorithm. This algorithm has stronger advantages in community detection， and the detected community is closer to the real community.

Key Words： cluster modularity; GA; SA; community detection

0 引言

许多现实世界都可以表示为网络，例如协作网络、万维网、生物网络等。网络可以用图表示，其中节点表示对象，边表示对象之间的关系[1]。近年来复杂网络备受关注。网络具有小世界、传递性等特征，其中社区结构是一个重要的特征。社区检测对于复杂网络研究具有重要意义，社区是图节点的一个子集，社区内节点之间的边相比其它社区更加紧密，而属于同一社区的节点属性相似度较高[2]。

社区检测最早用来解决图分割问题，其中最有代表性的就是Kernighan-Lin图分类算法，但是该算法需要提前知道网络社区规模，在现实生活中应用有一定难度[3]。基于Laplace矩阵的谱分法是一个典型代表，但该分类结果没有社区划分评价标准，无法确定划分的社区是否达到最优[4]。本文采用模块度作为社区划分好坏的评价标准，不仅解决了谱分类存在的问题，还改善了模块度由于分辨率限制导致社区检测结果不理想的问题。

模块度最初由Newman & Girvan引入，是GN算法的一个停止准则，现在已经成为许多社区检测算法的评价标准。模块化值越大，社区划分的效果就越好。因此，具有最大模块性的分区应该是最好的分区，这也是模块化寻求最大值的主要动机。但由于模块化优化过程中存在分辨率问题，所以加入一个可调参数，利用不同的分辨率进行社区检测。模块化在优化时无法识别较小的模块，这与网络的规模及模块中连接的紧密度有关。有学者提出了包含可调参数的通用函数，可以利用不同分辨率进行社区划分[5-6]。

遗传算法（GA）可用于优化模块化。首先随机生成一组解，将适应度高的个体挑选出来，这些个体进行重组或突变形成下一代个体，这样不断迭代，最后得到的个体适应性较高[7]。文化基因算法（MA）是Pablo Mosacato提出的一种算法，它将种群的全局搜索和个体的局部搜索结合，是目前广泛使用的一种算法。

本文提出一种社区检测算法，将GA算法与模拟退火算法结合，利用两种算法的优点识别网络结构，并将算法生成的网络与真实网络对比，证明算法的可行性。

1 网络模型概念

网络：就是若干元素的集合，这些元素是节点，把连接节点之间的关系叫做边。网络在生活中随处可见，通过边将一组节点连接起来是最简单的网络类型。在对地理环境进行建模时，图论提供了一个重要模型。

节点：一张图G由有限集合（V，E）构成，其中V表示节点集合，V={Vi|i=1，…n}，是网络的基础单元。在进行网络分析时，通常用带有某个属性的节点表示真实的个体，本文中的节点用来表示研究区域的村落，n=|V|为节点总数，即村落个数。

边：图中E表示边的集合，用来表示两个节点之间的关系，E={eij|Vi，Vj∈V}，m=|E|为边的总数。

邻接矩阵：Aij表示邻接矩阵，其值为1或0。当Aij为1时，表示节点i与节点j之间存在边。当Aij为0时，表示节点i与节点j之间不存在边[8]。

2 遗传模拟退火

2.1 遗传算法

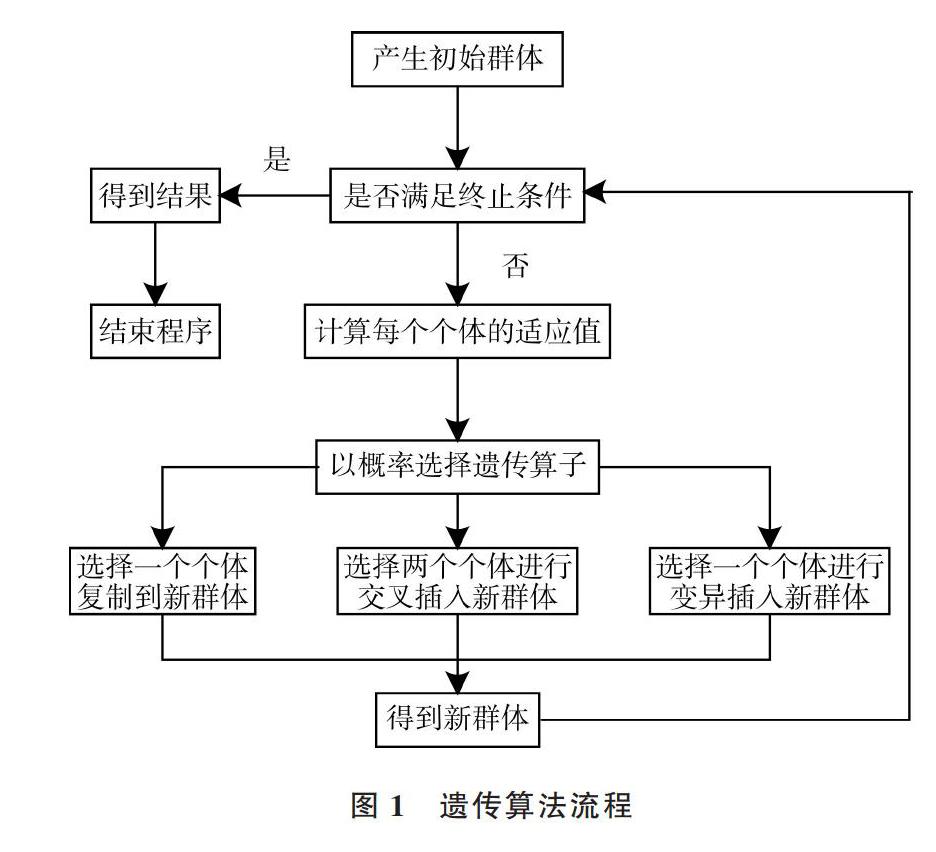
遗传算法（Genetic Algorithm）模拟生物进化形成的计算模型，生物进化中当产生下一代时存在自然选择和遗传变异，遗传算法在搜索最优解时模拟生物进化方式。通常从一组随机个体开始，在每一代种群中，对每个人的适应度进行评估，根据其适应性，从当前种群随机选择多个个体进行交叉、变异以形成新的群体。然后在算法的下一次迭代中使用新的群体。经过几次迭代，只有适应能力强的个体才能生存 [11]。遗传算法步骤如图1所示。

2.2 模拟退火算法

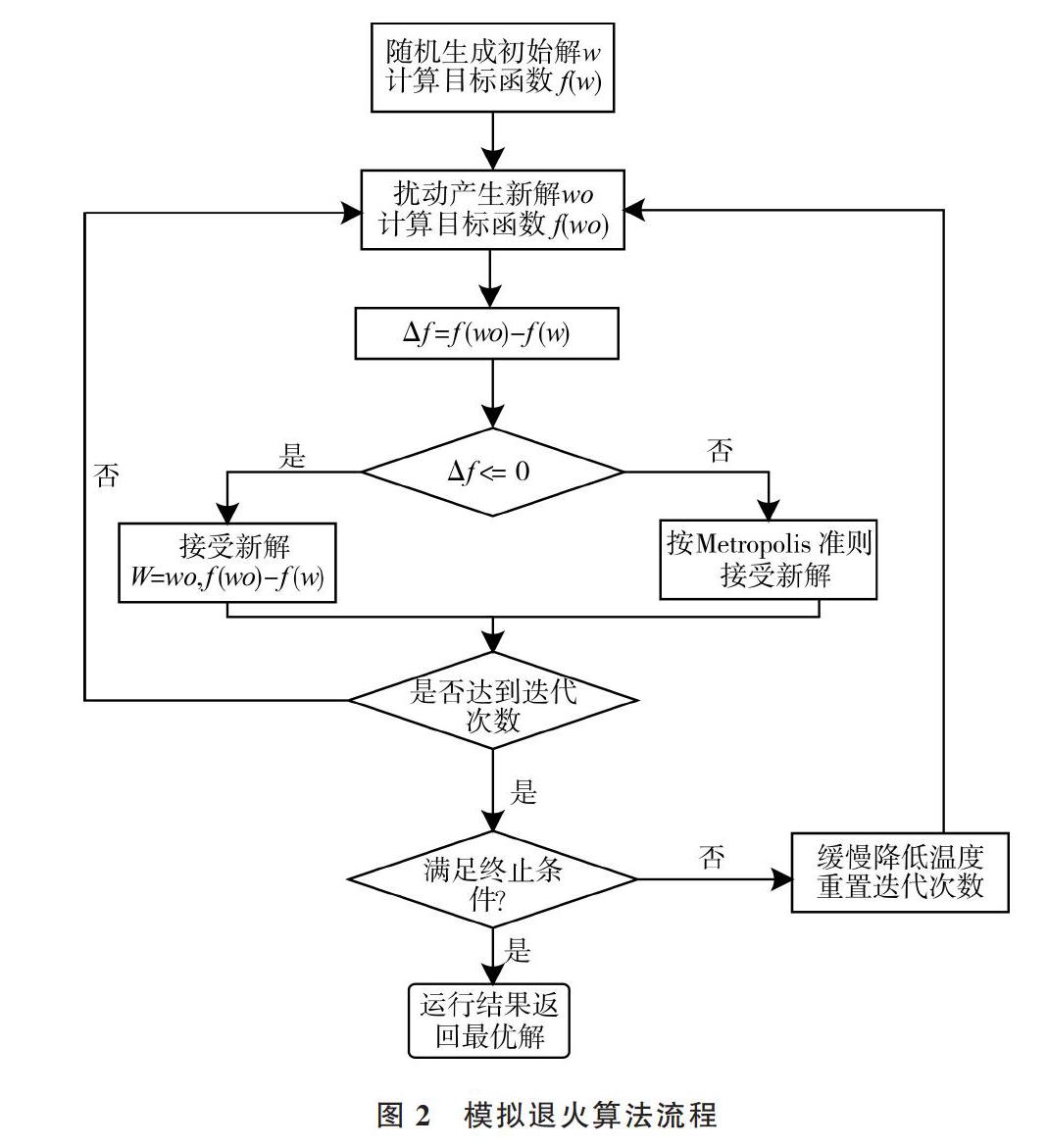
模拟退火（Simulated Annealing）由Metropolis在1953年提出，基于物理中固体物质的退火过程。模拟退火算法首先会设定一个很高的初始温度，当温度很高时突跳率也会很高，这有利于当前解跳出局部最优，随着温度降低突跳率会变低，当前解开始逐渐趋于全局最优[12]。模拟退火算法步骤如图2所示。

3 改进GASA算法

3.1 改进算法步骤

初始参数设置：①Gmax：最大迭代次数;Spop：种群大小;Spool：交配种群;Stour：旅行商大小;Pc交叉概率;Pm变异概率;②生成初始种群P;③随机选取Stour个个体进行比较，将适应度高的个体放入交配池。再从剩下的种群中挑选两个个体，选择其中适应度较高的个体放入交配池，不断进行此操作，直到种群中没有个体;④基因操作：从交配种群中挑选Pparent进行遗传变异操作，产生Pchild;⑤模拟退火操作：对Pchild进行模拟退火找到最优个体;⑥重复上述步骤，直到达到最大迭代次数;⑦更新最优解。

3.2 改进算法步骤说明

3.2.1 参数设置

3.2.2 初始化种群

一个网络被编码成为整数串x={x1x2…xn}，n是图中的顶点数，xi是顶点vi所在的簇，它可以是1到n的任意整数，有相同分类的点被分在相同的社区[13]。一个有n个顶点的图最多能分成n个簇，意思是每个簇最多包含一个顶点，可记作{1 2 …n}。需要注意的是不同的点可以分为同一类，例如一个图中有4个点，{3 1 2 3}和{1 2 3 1}都代表着相同的分类{{1，4}，{2}，{3}}，表示第1个和第4个点被分为一类。开始时，所有染色体上每个点都单独分为一类{1 2 …n}，但是最开始的基因缺少多样性而且计算的适应度很差，没有实际意义。初始化一个好的染色体基因能够加快收敛，节省时间，提高效率。对每个染色体先随机选取一个点，将这个点的分类类别赋给与它相连的点，然后重复这个操作α*n次，α=0.2，这样就能快速找到局部最好的分类，但是这样产生的初始解相对于最优解还是很差。

3.2.3 遗传变异

（1）遗传操作：传统方法是取两个个体，随机选择一个交叉点，将两个染色体中交叉点以后的全部元素交换，产生两个新的染色体[14]。但是这种直接交叉操作并不适合本算法。对于每个染色体，顶点簇是隨机的一个数字。

本文算法采用双向交叉操作，交叉结果步骤如下：①选择两个染色体Xa和Xb;②随机选择一个顶点Vi并确定顶点在染色体Xa上所在的簇xai，将染色体Xa上簇号为xai中所有顶点分配给染色体Xb相同的簇;③确定Vi在染色体Xb上所在的簇xbi，将染色体Xb上簇号为xai中所有顶点分配给染色体Xa相同的簇;④得到两个新的染色体Xc和Xd。

交叉操作以后产生具有双亲特征的子代，子代携带了父母的基因。

（2）变异操作：随机选择一个染色体进行突变，在染色体上找一个顶点，将顶点的簇改变为其邻居的簇。顶点的邻居即为与其相连的顶点，但是两个顶点所在的簇不同。重复操作n次，得到变异以后的染色体[15]。突变时，突变节点只可能变为与其相连节点的簇，减少了无用搜索。将遗传变异后的结果作为模拟退火的初始解，利用模拟退火搜索寻找最优解。

3.2.4 模拟退火搜索

（1）初始温度TT，最低温度Tmin，α为降温概率，初始状态xx=Pchild，最优解x_best=xx，评价函数f为模块密度。

（2）产生新解：将xx表示的图G划分为不同的簇，[Ω=V1，V2，？，Vm（2mn）]，m是簇的大小，n是顶点数，xx作为当前解。从Vi簇中选择一个顶点重新分配给另一个簇，产生新解x_new[16]。

（3）计算模块密度：计算当前染色体xx的模块密度fxx和产生的新解x_new的模块密度fx_new。

（4）接受新解作为当前解的概率：接受概率如式（3）所示[17]，如果接受新解作为当前解则xx=x_new，否则重复步骤（2）到步骤（4）。

①最优解更新：如果接受新解作为当前解时，需要将新的fxx与fx_best作比较，如果fxx比fx_best大，需要更新最优解，将xx值赋给x_bes，即x_best=xx，否则最优解不更新;②降低温度：TT=TT*α;③重复上述步骤，直到达到终止条件，结束程序[18]。

4 实验结果及分析

数据来源：实验数据采用Lancichinetti等提出的社区网络数据，网络中包含128个节点，这些节点划分为4个社区，每个社区包含32个节点，每个节点平均与16个节点相连，即节点平均度为16。但是与节点相连的其它节点可能与其在同一个簇也可能属于不同的簇，引入参数u，u代表与此节点相连的其它节点属于不同簇的比例。好的算法就是要发现社区中的结构，利用GASA算法来检测社区结构是否有效[19]。

评价函数如下：

（1）模块度公式指子图内部与外部度之差与子图大小的比率，模块度越大，分区效果越好，社区检测的目标就是不断寻找模块度的最大值。如式（4）所示，加入参数r，使得模块度具有一般性。

当r=0.5时，Dr与模块密度D大小相等，当r<0.5时，优化算法用来发现大社区，当r>0.5时，优化算法用来发现小社区，加入参数r后，避免了分辨率的限制。通过改变r的值分析复杂网络内部结构。

（2）NMI：是Leon Danon提出用来评价划分社区与已知社区之间差异性的指标。给定两个社区[a=（a1，a2，？][an）]，[b=（b1，b2，？bn）]，其中ap和bp表示第p个节点在两种社区划分中的社区编号，网络节点数量为n，NMI计算公式如下：

式（5）中，矩阵N的第i行元素之和用Ni表示，矩阵N第j列元素之和用Nj表示。NMI值越大表明社区划分效果越好，当NMI值为1时，表示利用算法划分的社区与原社区结构相同。

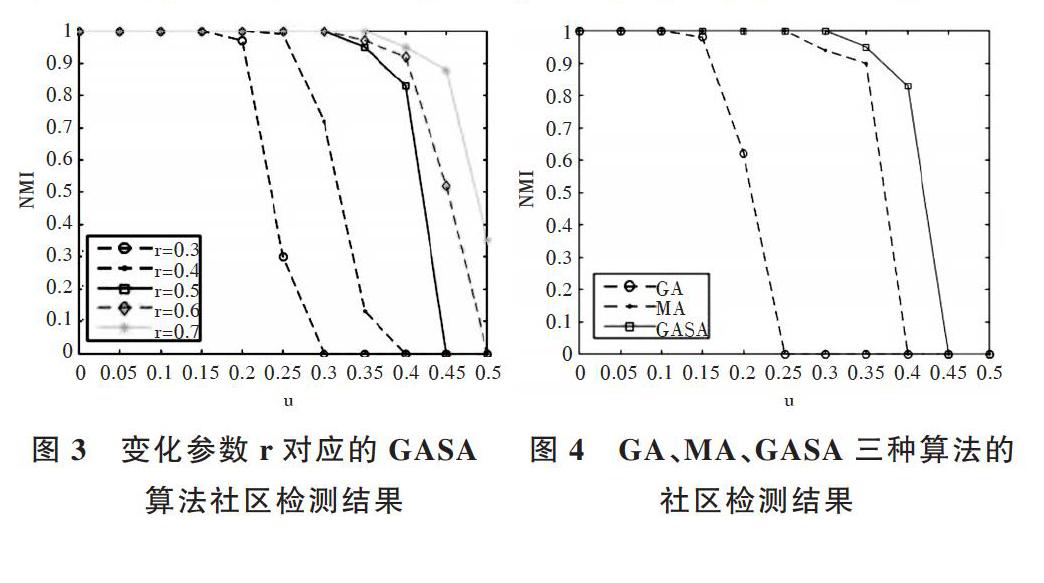
参数u取值范围是0～0.5，生成11个不同网络，利用NMI测试真实分区与算法检测到的分区之间的相似度，每个网络运行10次取平均值作为NMI的最终值。图（3）为当混合参数u从0增加到0.5时不同r值对应的NMI。当r=0.5、混合参数u值小于0.3时，算法可找到正确的社区划分。当u增加时，社区检测的正确度下降。u值为0.35时，NMI值为0.95;u值为0.4时，NMI值为0.9;当u值增大到0.45时，无法检测到真实社区。但是随着r值的增加，发现小社区的能力更强，r增大到0.7、u值为0.5时，NMI值仍能达到0.35。r值为0.3、u值达到0.3以后，此时NMI为0，社区检测结果为将整个社区划分为一个大社区。

将r值设置为0.5，分别用GA算法、MA算法、GASA算法进行社区检测，如图4所示。当u值小于0.1时，GA算法可以检测到真实社区;当u值小于0.25时，MA算法可以检测到真实社区;当u值小于0.3时，GASA算法可以检测到真实社区。虽然3种算法在u值增大到0.45时都无法检测到真实社区，但是在u值小于0.45时，本文提出的GASA算法较GA和MA算法却可以较好地检测到真实社区。

   

5 结语

本文提出的GASA改进算法能在社区检测时提高检测模块的密度值，将遗传算法与模拟退火算法相结合，实验表明GASA 比GA算法和MA算法在发现真实社区时更有优势。通过调整模块密度参数r，可以分析不同分辨率网络。未来研究工作主要是模块密度优化问题，避免人工调整参数r，将单一的模块密度优化问题转化为多目标优化问题。

参考文献：

[1] 陈争光，杨冬风. 特征选择与提取研究与应用[M]. 哈尔滨：黑龙江教育出版社， 2012：109-112.

[2] 张敏辉，赖麟，孙连海. 基于遗传算法的研究与Matlab代码实现 [J]. 四川教育学院学报，2012（1）：115-117.

[3] KERNIGHAN B W，LIN S. An efficient heuristic procedure for partitioning graphs[J]. Bell System Technical Journal，1970，49（2）：291-307.

[4] FORTUNATO S. Community detection in graphs[J]. Physics Reports，2010，486（3）：75-174.

[5] 陈颖，刘连光. 微网与智能配电网 [J]. 企业文化，2012（5）：46-48.

[6] 张炳达. 智能信息处理技术基础[M]. 天津：天津大学出版社，2008：98-102.

[7] 金志剛，徐珮轩. 密度峰值聚类的自适应社区发现算法[J]. 哈尔滨工业大学学报，2008（5）：44-51.

[8] 王耀南. 智能信息处理技术[M]. 北京：高等教育出版社，2003：178-184.

[9] 林顺刚. 遗传算法概述[J]. 科技信息，2007（2）：11-14.

[10] 石纯一，王家. 树立逻辑与集合论[M]. 北京：清华大学出版社，2000：198-2003

[11] 刘敬宇，朱朝艳. 遗传模拟退火算法在结构优化设计中的应用[J]. 吉林建筑工程学院学报，2010 （2）：5-8.

[12] 水超，李慧. 基于“次中心”的社区结构探索算法[J]. 计算机应用，2012 （8）：2154-2158.

[13] 张余. 随机能力提升下知识型员工调度问题研究[D]. 西安：西安电子科技大学，2012：33-38.

[14] 何云斌，张晓瑞，万静，等. 基于改进遗传模拟退火K-means的心电波形的分类研究[J]. 计算机应用研究，2014（11）：3328-3332.

[15] 陈丽，朱裴松，钱铁云，等. 基于边采样的网络表示学习模型[J]. 软件学报，2018（3）：756-771.

[16] 武兆慧，张桂娟，刘希玉. 基于模拟退火算法的聚类分析[J]. 计算机应用研究，2015（8）：24-26.

[17] 杨令兴，张喜斌. 基于单目标PSO的社区检测算法[J]. 计算机科学，2015（1）：57-60.

[18] 张健沛，姜延良. 一种基于节点相似性的连接预测算法[J]. 中国科技论文，2013（7）：659-662.

[19] 杨冬旺. 基于遗传模拟退火算法的热泵和制冷系统优化[D]. 天津：天津大学，2007：34-36.

（责任编辑：杜能钢）