Dynamical Analysis and Exact Solutions of a New(2+1)-Dimensional Generalized Boussinesq Model Equation for Nonlinear Rossby Waves∗
2019-10-17QuanShengLiu刘全生ZaiYunZhang张再云RuiGangZhang张瑞岗andChuangXiaHuang黄创霞SchoolofMathematicalSciencesInnerMongoliaUniversityHohhot0002China
Quan-Sheng Liu(刘全生),Zai-Yun Zhang(张再云), Rui-Gang Zhang(张瑞岗), and Chuang-Xia Huang(黄创霞)School of Mathematical Sciences,Inner Mongolia University,Hohhot 0002,China
2School of Aeronautics Science and Engineering,Beihang University,Beijing 100191,China
3School of Mathematics,Hunan Institute of Science and Technology,Yueyang 414006,China
4Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering Changsha University of Science and Technology,Changsha 410014,China
5School of Mathematics and Statistics,Changsha University of Science and Technology,Changsha 410014,China
(Received March 24,2019;revised manuscript received May 27,2019)
AbstractIn this paper,we study the higher dimensional nonlinear Rossby waves under the generalized beta effect.Using methods of the multiple scales and weak nonlinear perturbation expansions[Q.S.Liu,et al.,Phys.Lett.A 383(2019)514],we derive a new(2+1)-dimensional generalized Boussinesq equation from the barotropic potential vorticity equation.Based on bifurcation theory of planar dynamical systems and the qualitative theory of ordinary differential equations,the dynamical analysis and exact traveling wave solutions of the new generalized Boussinesq equation are obtained.Moreover,we provide the numerical simulations of these exact solutions under some conditions of all parameters.The numerical results show that these traveling wave solutions are all the Rossby solitary waves.
Key words:generalized Boussinesq model equation,nonlinear Rossby waves,dynamical analysis,traveling wave solutions,nonlinear perturbation expansions,bifurcation theory of planar dynamical systems
1 Introduction
It is well known that the complex physical process of the atmospheric and the oceanic motions is affected by multiple factors,such as the background current,the bottom topography,the external temperature source,and the turbulent dissipation.There are many kinds of wave phenomena with different scales in the real atmosphere and ocean,such as the acoustic waves,the inertial waves,the gravity waves,and the Rossby waves and so on.Specially,the Rossby waves,which describe the main characteristics of long-term weather or climate phenomena,play an important role in the planetary scale oceanic and atmospheric motions,see Refs.[1–7].One distinctive fact is that they contain stable and large solitary waves.This provides better explanations to the physical mechanisms of some weather activities,such as the Jupiter’s Great Red Spot and atmospheric block.[8]In recent years,based on the quasi-geostrophic theory,many researchers investigated the Rossby waves of the planetary scale oceanic and atmospheric motions and obtained several types of nonlinear partial differential equations(NPDEs).These equations include the Korteweg-de Vries(KdV)equation,the modified Korteweg-de Vries(mKdV)equation,the Benjamin-Davis-Ono(BDO)equation,the Boussinesq equation and so on,see Refs.[9–20].
From what is mentioned in the previous part,we come to know that the mathematical models describing nonlinear Rossby waves are merely(1+1)-dimensional cases.More recently,investigations on higher dimensional nonlinear Rossby solitary waves attract more and more attention from the researchers.In plasma and shallow water waves,some researchers generalized the KdV equation and the mKdV equation to the higher dimensional cases,namely,the Kadomtsev-Petviashvili(KP)and Zakharov-Kuznetsov(ZK)equation.[21−25]In shallow water model,based on irrotational assumption,Johnson[26]studied the(2+1)-dimensional Boussinesq equation and showed the evolution of gravitational surface waves.Using surface water wave theory,Mitsotakis[27]studied the higher dimensional Boussinesq equation with a variable bottom and simulated propagation of the waves.In the field of geophysics,some researchers[28−32]investigated ZK equation from the quasi-geostropic potential vorticity equation and showed the physical mechanisms of the nonlinear Rossby waves.However,to the best of our knowledge,there is no report with respect to the higher dimensional Boussinesq equation in the study of the nonlinear Rossby waves.
It is very important to construct explicit solutions of the NPDEs.Recently,many efficient methods have been developed to find the solutions of the NPDEs,such as the trigonometric function series method,[33]the improved tan(ϕ(ξ)/2)-expansion method,[34]the sinecosine algorithm,[35]the Wronskian technique,[36]the formally variable separation approach,[37]the Septic B-spline method,[38]the transformed rational function method,[39]the symmetry algebra method(consisting of Lie point symmetries),[40]the mesh-free method,[41]the homotopy perturbation method,[42]the modified mapping method and the extended mapping method,[43]the bifurcation method and qualitative theory of dynamical systems,[44]the multiple exp-function method,[45]the modified trigonometric function series method,[46]the modified(G’/G)-expansion method,[47]infinite series method and Jacobi elliptic function method,[48−49]RBF approximation method,[50](G′/G−1/G)-expansion method,[51]Hirota bilinear method,[52−54]lattice Boltzmann method,[55−56]and so on.In this paper,we will derive(2+1)-dimensional Boussinesq equation from the quasi-geostropic potential vorticity equation with the generalized beta effect.By using the bifurcation theory of planar dynamical systems and the qualitative theory of ordinary differential equations,we obtain the dynamical analysis and exact traveling wave solutions of the new Boussinesq equation.
Based on the above discussions,we will take into account a new Boussinesq equation for nonlinear Rossby waves. The paper is organized as follows. In Sec.2,we are interested in the derivation of the new Boussinesq equation for nonlinear Rossby waves from the barotropic quasi-geostropic equation with the generalized beta effect.In Sec.3,we investigate the dynamical behaviours of the new Boussinesq equation and obtain its exact traveling wave solutions.Finally,some conclusions are presented in Sec.4.
Remark 1In Ref.[1],the authors considered the(2+1)-dimensional nonlinear Rossby waves under non-traditional approximation.Based on the asymptotic methods of multiple scales and weak nonlinear perturbation expansions,they obtained a new modified Zakharov-Kuznetsov equation from the barotropic potential vorticity equation with the complete Coriolis parameter,the topography and the dissipation.Using the new auxiliary equation method,they established new exact solutions without dissipation effect.In the situation of dissipative effect,they investigated the propagation of Rossby waves with different parameters by using the homotopy perturbation method.In Ref.[5],Lu et al.investigated(2+1)-dimensional timefractional Boussinesq equation by using the multi-scale analysis and perturbation method.Also,they obtained the exact solutions by using the improved(G′/G)expansion method as well as Lie group analysis method without dissipation effect.Furthermore,with dissipation effect,they considered the approximate solutions by adopting the New Iterative Method.
2 Derivation of New Boussinesq Equation
Starting from the quasi-geostrophic vorticity equation with the generalized beta effect and the dissipation effect,the equation can be written as[57]

where ψ is the total stream function,f=f0+ β(y)y is the vertical component of Coriolis parameter with f0=2Ωsinφ0(Coriolis parameter should be small vorticity),Ω is the angular of the earth rotation and φ0is the local latitude. β(y)is generalized Rossby parameter,[58]µis the turbulent dissipation parameter,Q denotes the external heating source and∇2is the two-dimensional Laplace operator.Equation(2)denotes no penetration boundary conditions.
We introduce some dimensionless parameters as follows:

Here,dimensionless variables are marked by an asterisk.L0is the zonal characteristic length,H is a vertical characteristic length,and U0is the characteristic velocity.
Substituting Eq.(3)into Eqs.(1)and(2)yields
Here,we omit the asterisks of the superscript for the sake of convenience.
In the case of weakly nonlinear disturbances,the form of total stream function is assumed as

It follows from Eqs.(4)and(6)that
where

and

is the Jacobi operator.Meanwhile,to strike a balance between dispersion and nonlinearity,we assume that

In order to take into account the effects of nonlinearity and amplitude modulation of the Rossby waves,we introduce the slow time and space variables as follows
where 0< ε≤ 1,and ε is small for weak nonlinearity.The derivative transformations of Eq.(9)are
We expand the perturbation stream function ψ′as follows
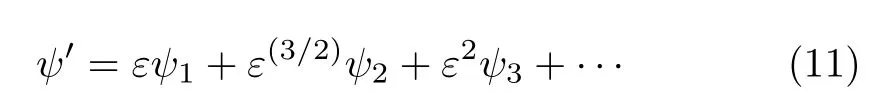
Plugging Eqs.(8),(10),and(11)into Eq.(7)leads to all order perturbation equations about ε:

Assume that Eq.(12)has the formal solution as follows
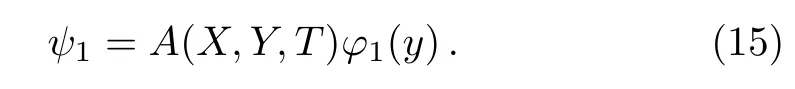
It follows from Eqs.(12)and(15)that
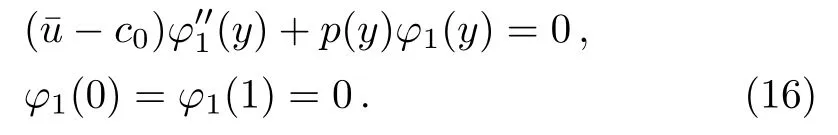
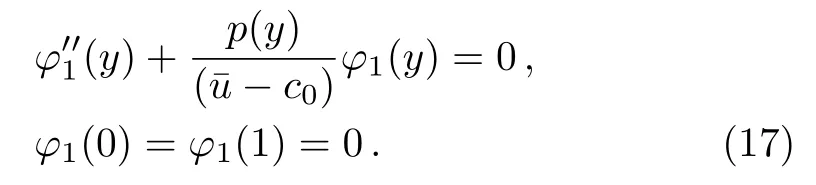
Equation(17)is the Rayleigh-Kuo equation,which determines the meridional structure of the waves.We need to solve higher order equations to determine the evolution of amplitude A(X,Y,T)with time and space.
Assume that Eq.(13)has the formal solution as follows

where
Utilizing the separable variables method,we obtain from Eqs.(13),(18),and(19)that

Set
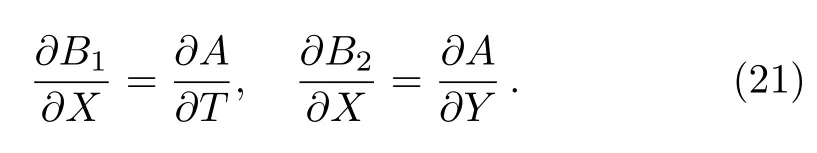
Then,from Eq.(20),we get the following equations:

and

Obviously,according to Eqs.(22)and(23),we have

Substituting Eqs.(15),(18),and(21)into Eq.(14)yields the following equation
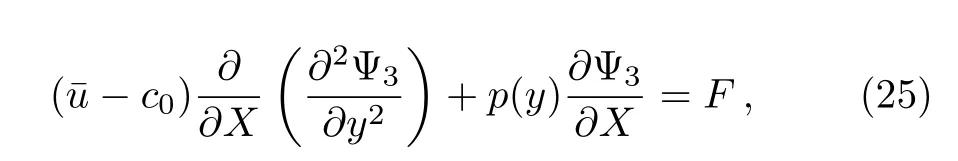
where

Obviously,Eqs.(17)and(25)have the same homogeneous part.In order to obtain a regular solution to Eq.(25),we need the assumption of the non-singular condition as follows

Plugging Eqs.(16),(21),(22),and(23)into Eq.(26)yields
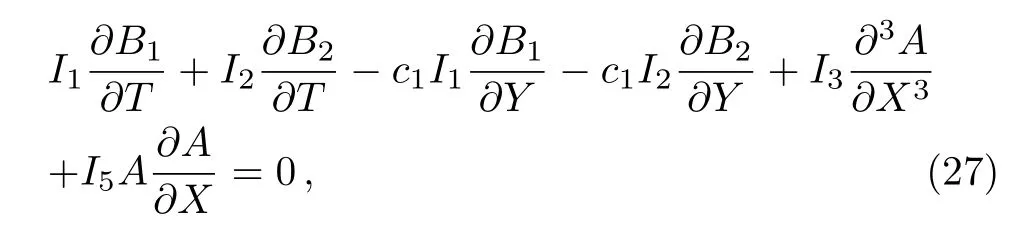
where the coefficients are
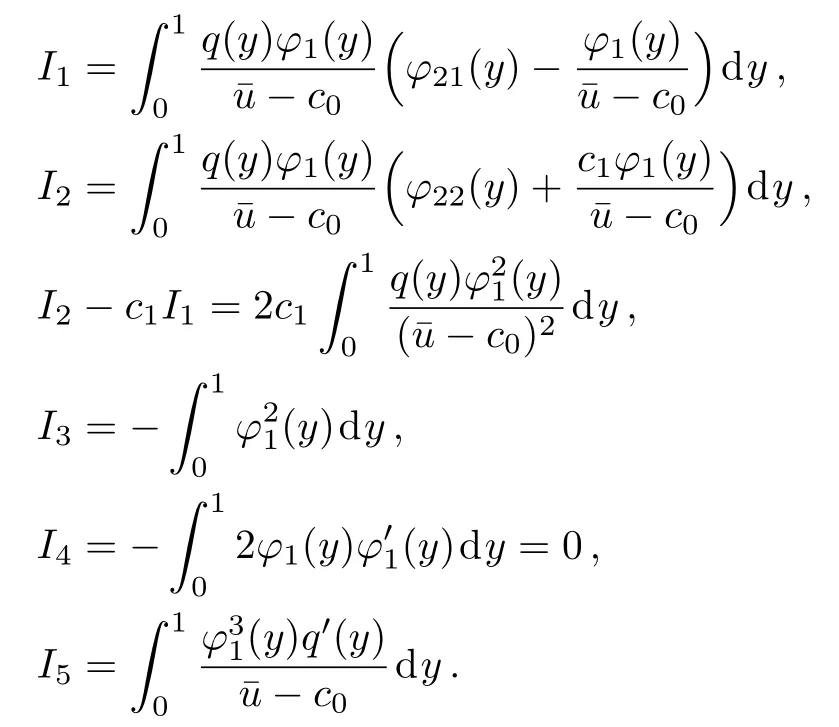
From Eq.(27),we get

where
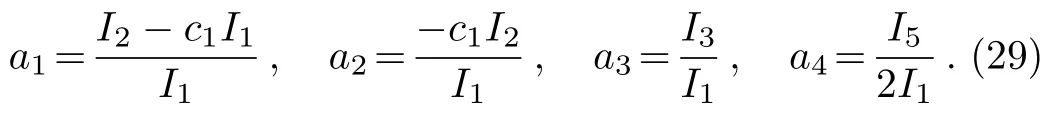
Now,we have obtained the spatial-temporal structure equation for wave amplitude A(X,Y,T).When I2=c1I1,namely,a1=0,Eq.(28)degenerates to the(2+1)-dimensional standard Boussinesq equation.Otherwise,Eq.(28)is the generalized Boussinesq equation under the generalized Rossby parameter(i.e.a1̸=0).
3 Dynamical Analysis and Exact Solutions for the New Boussinesq Equation
In this section,benefited from some ideas of Ref.[44],that is,bifurcation theory of planar dynamical systems and the qualitative theory of ordinary differential equations,we show the dynamical analysis and obtain the exact solutions to the new Boussinesq equation.
Let A= ϕ(ξ), ξ=mX+nY+lT,then Eq.(28)becomes

where g is the integration constant.
Letting ϕ′=y,we obtain the planar system as follows
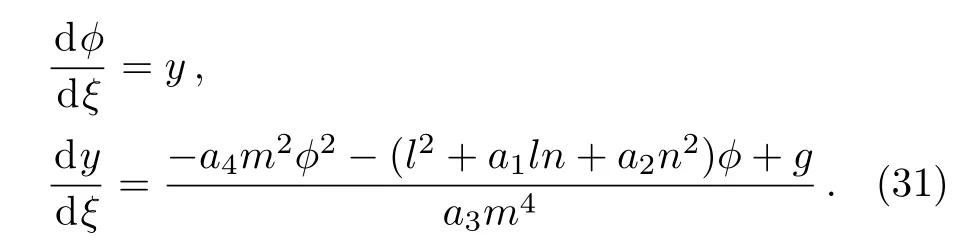
It is easy to see that Eq.(31)has the follow Hamiltonian function

where h is the integration constant.
Assume that
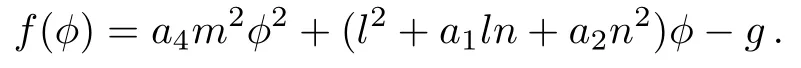
Thus,in order to investigate the distribution of singular points of Eq.(31),we obtain the fixed points of f(ϕ).
When ∆ :=(l2+a1ln+a2n2)2+4a4m2g>0,f(ϕ)has two fixed points ϕ1,ϕ2as follows

When f′(ϕ)=0,we obtain
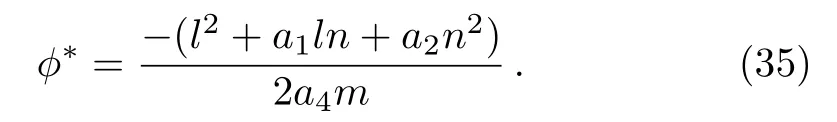
Let g0=|f(ϕ∗)+g|,then g0is the extreme values of f(ϕ)+g.
Letting(ϕi,0)(i=1,2)be one of the singular point of system of Eq.(31),then the characteristic values of the linear system of Eq.(31)at two singular points(ϕi,0)are
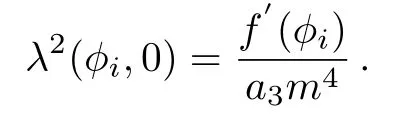
From the qualitative theory of dynamical systems,[44]we have
Thus,based on the above analysis,we get the bifurcation phase portraits of Eq.(31)as Figs.1 and 2.
Next,due to the qualitative theory of dynamical system,we deduce the traveling wave solutions to Eq.(31).Furthermore,we divide our arguments into two cases.
Case 1g=0.

Fig.1 The bifurcation phase portraits of Eq.(31)when l2+a1ln+a2n2>0.
When g=0,Eq.(31)reduces to the system as follows
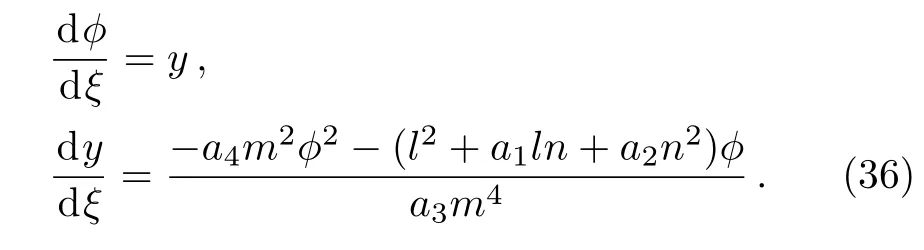
From Figs.1 and 2,we observe that Eq.(31)has a homoclinic orbits Γ1(see Fig.3).
In ϕ − y plane,Γ1is described as
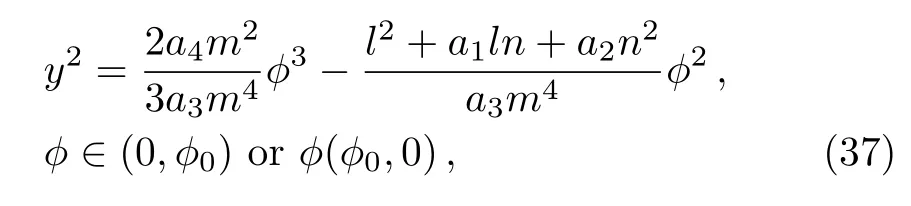
where ϕ0=(3(l2+a1ln+a2n2))/(2a4m2).It follows from Eqs.(36)and(37)that
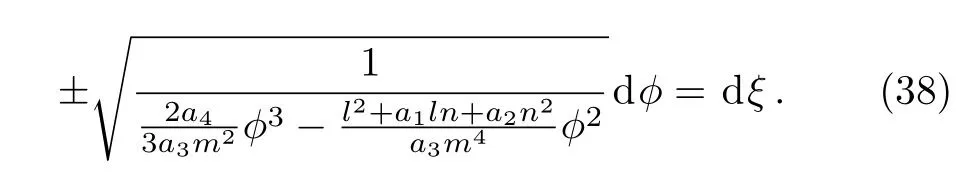

Fig.3 Homoclinc orbits when a3/(l2+a1ln+n2)<0.
Assuming that ϕ(0)= ϕ0and integrating Eq.(38)
along homoclinic orbit Γ1,we obtain

From Eqs.(39)and(40),we get
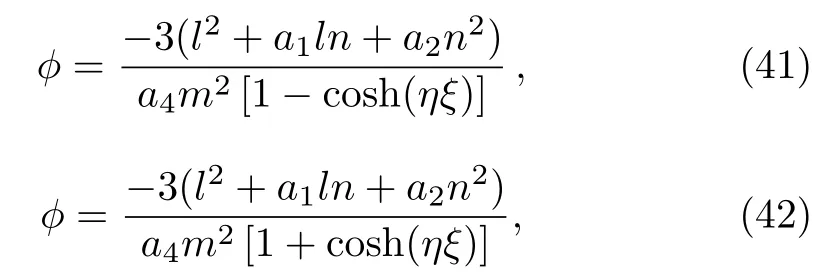
From Eq.(41)and Eq.(42)and traveling wave transformation

we obtain the solitary wave solutions

See Fig.4.

Fig.4 The diagrammatic sketch of the solutions of the case 1 with m=n=1,l=−1,a1=a2=0.01,a3=−0.01,a4=10.(a)u1(ξ),(b)u2(ξ).
Similarly,we can obtain the other solitary wave solutions

See Fig.5.
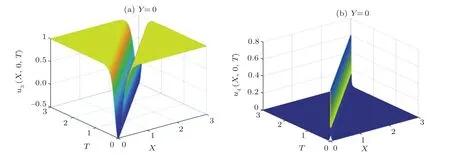
Fig.5 The diagrammatic sketch of the solutions of the case 1 with m=n=1,l=−1,a1=a2=a3=0.01,a4=1.(a)u3(ξ),(b)u4(ξ).
Case 2g≠0.
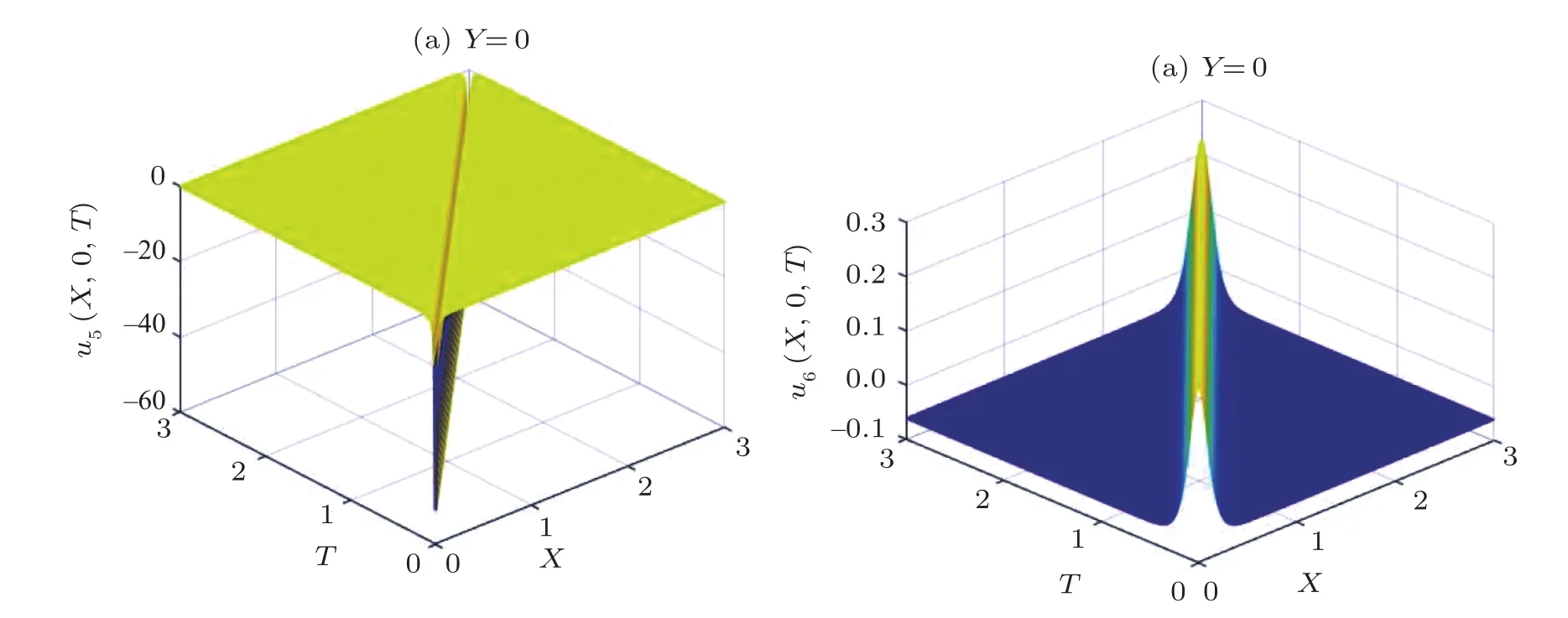
From Fig.1 to Fig.2,we observe that Eq.(31)has a homoclinic orbit Γ2.See Fig.6.
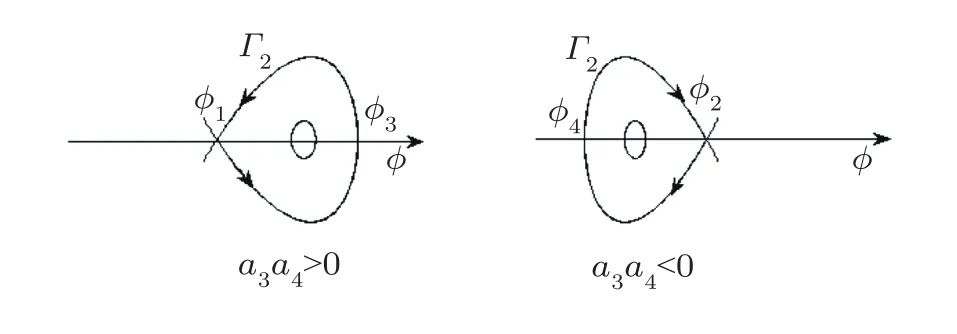
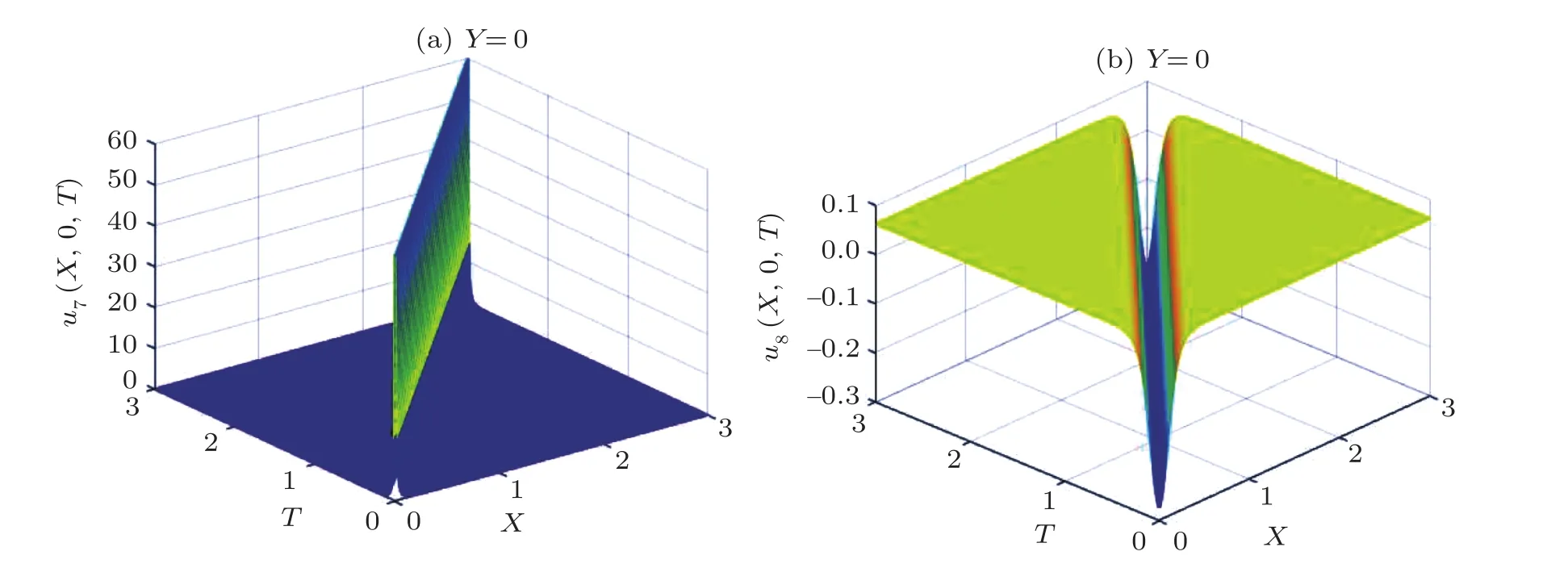
Fig.6 Homoclinc orbits when 0<−g In ϕ − y plane,Γ2is described as where h=H(ϕi,0),i=1,2, It follows from Eqs.(31)and(47)that Assuming that ϕ(0)= ϕ3and integrating Eq.(48)along homoclinic orbit Γ2,we have By Eqs.(49)and(50),we obtain See Fig.7. Similarly,we can deduce that solitary wave solutions See Fig.8. From Figs.4,5,7,8,it can be seen that these traveling wave solutions are all Rossby solitary waves. Fig.7 The diagrammatic sketch of the solutions of the case 2 with m=n=1,l=−1,a1=a2=0.1,a3=−0.01,a4=10,g=0.1.(a)u5(ξ),(b)u6(ξ). Fig.8 The diagrammatic sketch of the solutions of the case 2 with m=n=1,l=−1,a1=a2=0.1,a3=0.01,a4=10,g=0.1.(a)u7(ξ),(b)u8(ξ). In this paper,firstly,we derive a new(2+1)-dimensional generalized Boussinesq equation with generalized beta effect from the barotropic potential vorticity equation by using methods of the multiple scales and weak nonlinear perturbation expansions.Secondly,borrowing from the ideas of Ref.[44],we present the dynamical analysis and obtain exact traveling wave solutions of the new generalized Boussinesq equation.Finally,we show the simulations of the bifurcation phase portraits and the exact traveling wave solutions under some conditions of some parameters.Indeed,in our contribution,Eq.(30)is equivalent to the following ordinary differential equation where P,Q,and R are constants and g is the integral constant. However,in Ref.[44],under traveling wave transformation,we observe that the authors investigated ordinary differential equation and considered the integral constant g=0.Thus,based on the ideas of our paper,we can also investigate the dynamical analysis and obtain exact traveling wave solutions of Eq.(55)in the future research. We would like to thank two anonymous reviewers for their comments,which have helped to improve the presentation of this manuscript substantially.

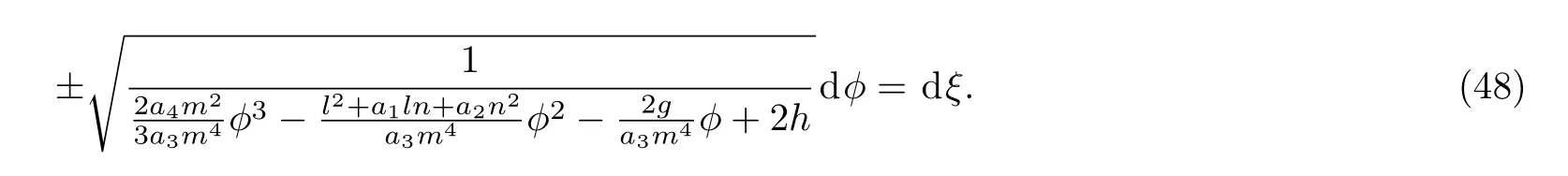



4 Conclusion


Acknowledgments
杂志排行
Communications in Theoretical Physics的其它文章
- DKP Equation with Energy Dependent Potentials
- Effective Correlation of Two Holes in a Semimagnetic Quantum Well Wire:Influence of Shape of Confining Potential on Coulomb Interaction∗
- Scale-Invariance Exists in the Series of Character Intervals in the Four Great Chinese Novels∗
- A Statistical Mechanical Analysis on the Bound State Solution of an Energy-Dependent Deformed Hulthn Potential Energy∗
- Study on the Amyloid Aβ42 with Accelerated Molecular Dynamics Simulations∗
- Inflationary Cosmology with Quantum Gravitational Effects and Swampland Conjectures∗
