全级配混凝土抗拉性能的随机特性及数值分析

何 吉 章嘉伟 徐小雪,2 曹 果 叶 开

(1.武汉大学 水利水电学院,武汉 430072;2.江西省水利规划设计研究院,南昌 330029)

全级配混凝土,是大型水工建筑物的核心建筑材料,作为脆性材料,其抗拉强度远低于抗压强度,因此研究全级配混凝土的抗拉性能对水工建筑物的安全性和耐久性至关重要.

随机特性是混凝土的固有属性,主要表现在以下几方面：1)骨料的空间分布及几何形状具有随机性,主要由骨料开采、混凝土振捣等的不确定性引起;2)砂浆的力学性能具有随机性,主要由砂浆的拌和、水化成熟度等的不均匀性引起;3)骨料与砂浆之间界面的力学性能具有随机性,主要由骨料表面粗糙度、砂浆力学性能等的不均匀性引起.上述随机特性可能引起混凝土的宏观力学性能出现较大波动,从而严重影响工程设计时的参数取值,因此研究全级配混凝土抗拉性能的随机特性具有重要意义.

测定全级配混凝土单轴抗拉强度的物理实验方法目前主要有直接和间接两种.直接方法中,采用试验机对全级配混凝土大试件直接加载,测定其抗拉强度[1].由于试件的尺寸较大,达到45 cm×45 cm×90 cm[2],导致设备要求较高,实验难度较大,成本较高,通常三峡[3]、二滩[4]、葛洲坝[5]等重点工程才有能力进行.对于大多数中小型工程而言,一般采用间接方法,即仅进行湿筛二级配小试件试验,将试验结果乘以强度折减系数[6],从而推测全级配混凝土的抗拉强度,但是由于折减系数具有较大的离散性[7],因此间接方法的使用存在局限性.

随着计算机性能的提高以及计算力学理论的发展,数值试验逐渐被用于全级配混凝土抗拉性能的研究中.数值试验具有成本低、操作便捷、可重复性高等优点,是物理实验的有益补充.目前的数值试验中主要考虑骨料的几何随机性对混凝土力学性能的影响.荆帅召[8]、任朝军[9]分别建立了全级配和三级配混凝土细观数值模型,模拟了混凝土单轴受拉破坏试验,试验结果表明随机多边形骨料及其分布形式直接影响混凝土的力学性能.已有研究[10-11]表明,砂浆、界面的力学特性对混凝土具有较大影响,但是现有的数值试验[12-13]中通常将砂浆、界面的材料参数赋予定值,忽视了砂浆、界面力学性能的随机性.

为了研究骨料、砂浆及界面的随机特性对混凝土抗拉性能的综合影响,本文首先基于骨料级配曲线、Weibull分布理论以及有限单元法,建立50组随机试件的数值模型;然后,分别进行单轴拉伸数值试验,得到相应的宏观应力应变曲线,基于该曲线进一步得到混凝土的弹性模量、峰值应变和极限抗拉强度;最后,采用随机分析和可靠度理论,研究骨料、砂浆及界面的随机特性对上述参数的影响,探讨数值分析中同时考虑骨料、砂浆及界面随机性的必要性.

1 数值试验

1.1 数值模型生成

本文采用二维数值模型,研究全级配混凝土的随机特性.对于二维问题,一般采用瓦拉文公式建立骨料的合理级配[14-15].全级配混凝土中骨料按粒径分为特大石(80～150 mm)、大石(40～80 mm)、中石(20～40 mm)、小石(5～20 mm).取上述粒径的均值,基于瓦拉文公式得到各粒径骨料的颗粒比为1∶4∶10∶70.由于篇幅所限,具体计算过程及相关公式可参考文献[14].需要特别说明的是为了简化计算,本文不单独考虑粒径小于5 mm的细骨料,其作用通过砂浆的材料参数来等效地反应[14].

数值模型中,骨料的随机投放过程如下[15]：首先,采用蒙特卡罗方法生成颗粒的形心位置,得到圆形骨料的随机分布;然后,在圆形骨料中内接多边形,并将各边外扩,直至多边形的面积等于圆形骨料的面积;最后,形成多边形骨料的随机分布模型.

混凝土通常被认为是骨料、砂浆及两者界面组成的非均质材料.界面作为弱面,其弹模及强度相对较小,对混凝土的抗拉强度具有重要影响,因此界面的准确模拟至关重要.本文在数值模型中将界面视为骨料延伸出的覆盖层,根据纳米压痕试验的结果,将界面厚度取为50μm[16].采用四边形单元划分网格,生成的全级配混凝土二维细观有限元模型[2]如图1所示.

图1 全级配混凝土试件数值模型

1.2 细观损伤模拟

混凝土的损伤过程可以描述为：材料的初始缺陷在外荷载作用下首先发展成微裂纹,之后逐渐演变成宏观裂缝,最终导致混凝土发生破坏[17].本文采用有效应力法定义混凝土的损伤变量,当不考虑泊松比的损伤时,弹性模量E服从

式中,E为损伤后的弹模;E0为未损伤时的弹模;d为损伤系数.

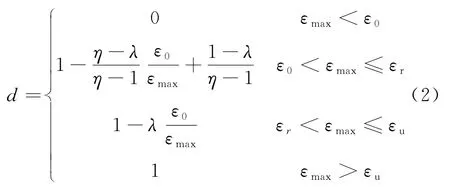
本文假定砂浆和界面服从双折线弹性损伤模型[18-19],如图2所示[20],数学表达式见式(2).该模型描述了数值模拟中当拉应力达到极限抗拉强度ft时,单元开始损伤,材料强度随损伤而降低,直至达到残余强度ftr.式中,ε0为单元应力达到极限抗拉强度时的主拉应变,即峰值应变;εr为单元应力达到残余抗拉强度时的主拉应变,等于ηε0,η为残余应变系数;λ为残余强度系数;εu为极限主拉应变,等于ξε0,其中ξ为极限应变系数;εmax为历史最大主拉应变,等于

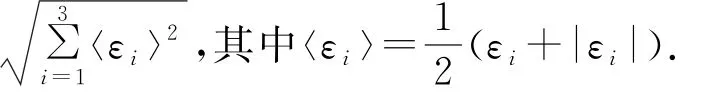
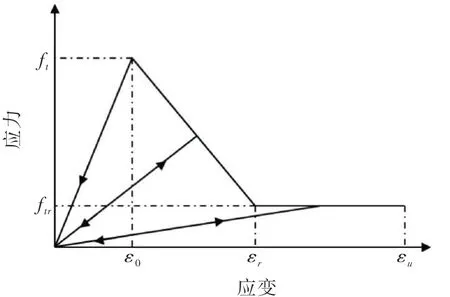
图2 双折线弹性损伤模型

1.3 参数标定

徐小雪[2]根据CorrD等的单骨料混凝土物理试验成果[21],通过数值试验与物理试验的对比(如图3～4所示),标定了一套损伤力学参数,具体取值如下：砂浆、骨料和界面的弹性模量分别为25 GPa、60 GPa与20 GPa,泊松比均为0.2且始终恒定不变;峰值应变ε0、η、λ见表1[2].

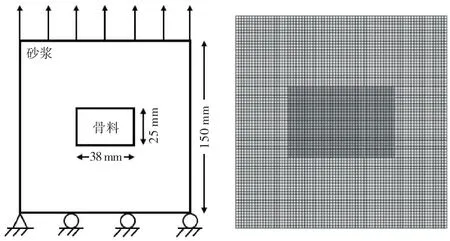
图3 单骨料混凝土试件的尺寸及有限元网格

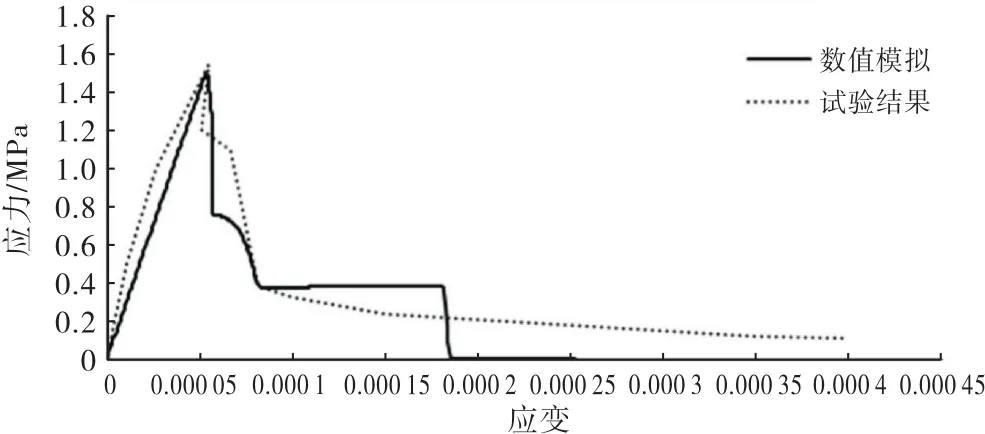
图4 单骨料混凝土试件的应力-应变曲线

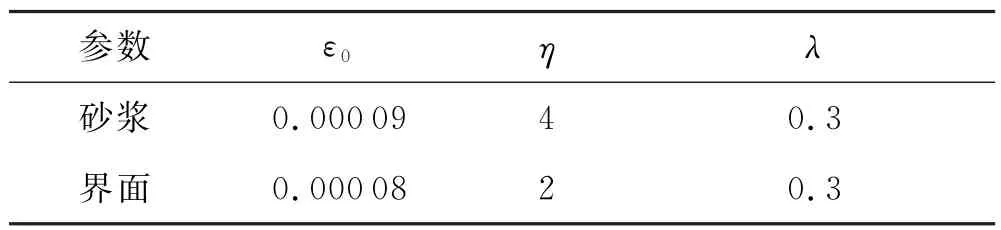
表1 损伤力学参数表

对于砂浆及界面,考虑其力学性能的随机性.基于唐春安[19]等对混凝土细观力学参数的研究,采用Weibull模型(式(3))描述砂浆及界面的力学参数,Weibull参数见表2.

表2 Weibull模型参数表

由于骨料的强度远大于砂浆及界面,同时为了简化计算,所以借鉴Unger[22]、荆帅召[23]等的假定,认为骨料始终为线弹性(不发生损伤),且具有恒定的弹性模量和泊松比.因此本文仅考虑骨料随机投放产生的几何随机性(即考虑骨料的随机分布及随机形状),而不考虑骨料力学性能的随机性.表1及表2中的参数将用于后续数值计算.

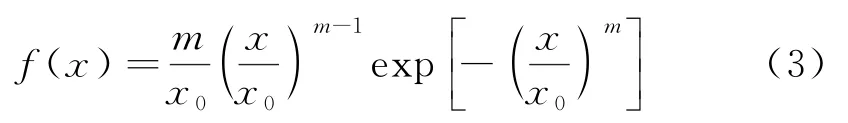
式中,x0为尺度参数;m为形状系数.

2 试验结果

2.1 砂浆及界面随机性的影响

基于Weibull分布模型,对砂浆、界面的力学参数进行抽样,共得到10组参数,保持骨料的分布及形状不变,研究砂浆、界面的力学随机性对混凝土宏观力学性能的影响.10组试验对应的宏观应力应变曲线如图5所示,由图确定的弹性模量、峰值拉应变及极限抗拉强度见表3.为了节省计算时间,当应力应变曲线出现明显的下降段时,即停止计算,所以图5中并没有提供完整的应力应变曲线(下文相同).

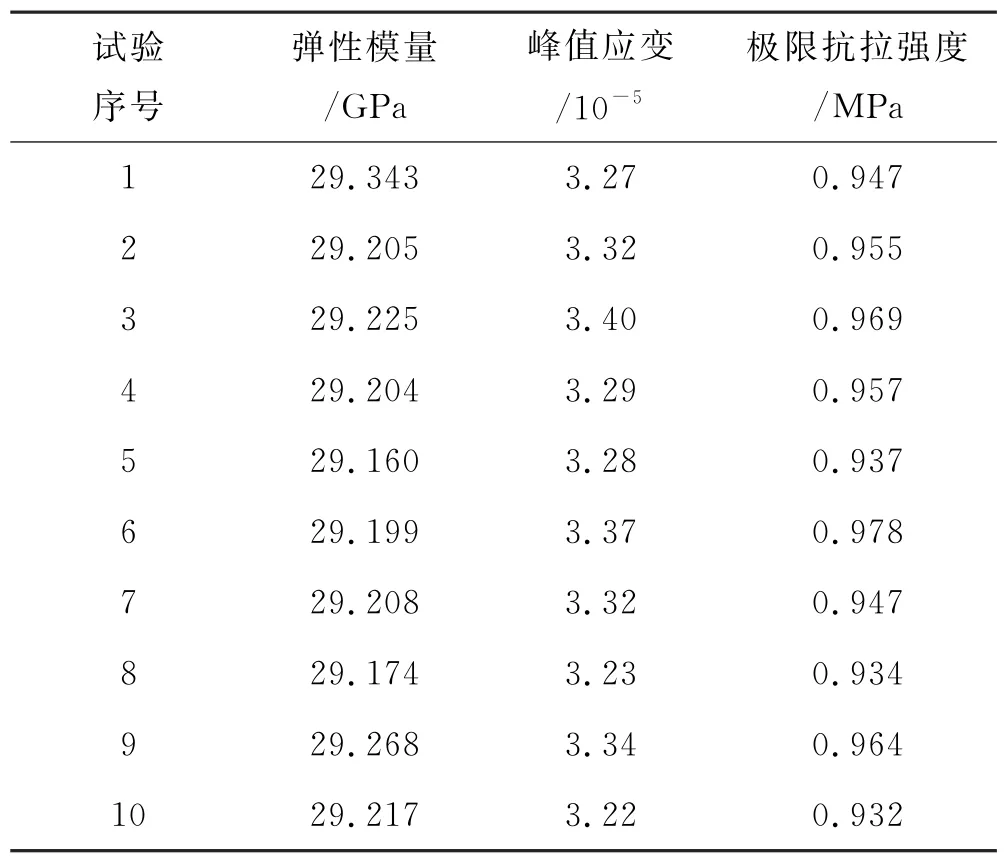
表3 砂浆及界面的随机性对混凝土抗拉性能的影响

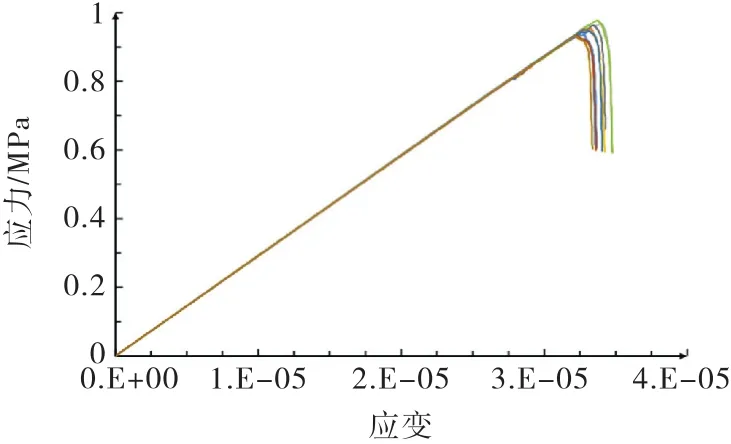
图5 砂浆及界面的随机性对混凝土应力应变曲线的影响

为了评判随机性的影响程度,定义指标ζ：

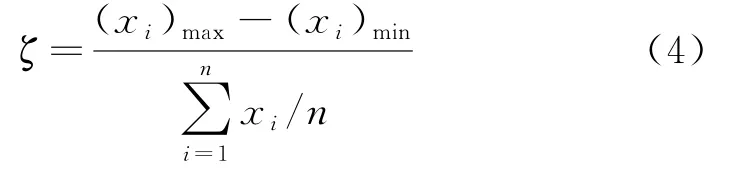
式中,x i为试验结果,即弹性模量、峰值应变或极限抗拉强度;i为试验序号;n为试验总次数.

由表3及式(4)得到,砂浆、界面的力学随机性对弹性模量、峰值应变和极限抗拉强度的影响程度分别为0.63%、5.4%和4.8%,即对弹性模量的影响最小,对峰值应变和极限抗拉强度的影响相似.

2.2 砂浆、界面及骨料的随机性影响

采用Weibull分布模型,对砂浆、界面的力学参数进行抽样,同时采用蒙特卡洛方法,对骨料进行随机投放,即对骨料的分布位置及几何形状进行抽样,共得到50个试件,分别进行数值试验,得到的混凝土应力应变曲线如图6所示,由图确定的弹性模量、峰值应变及极限抗拉强度见表4～6.

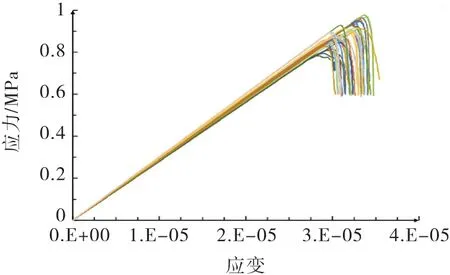
图6 砂浆、界面及骨料的随机性对混凝土应力应变曲线的影响

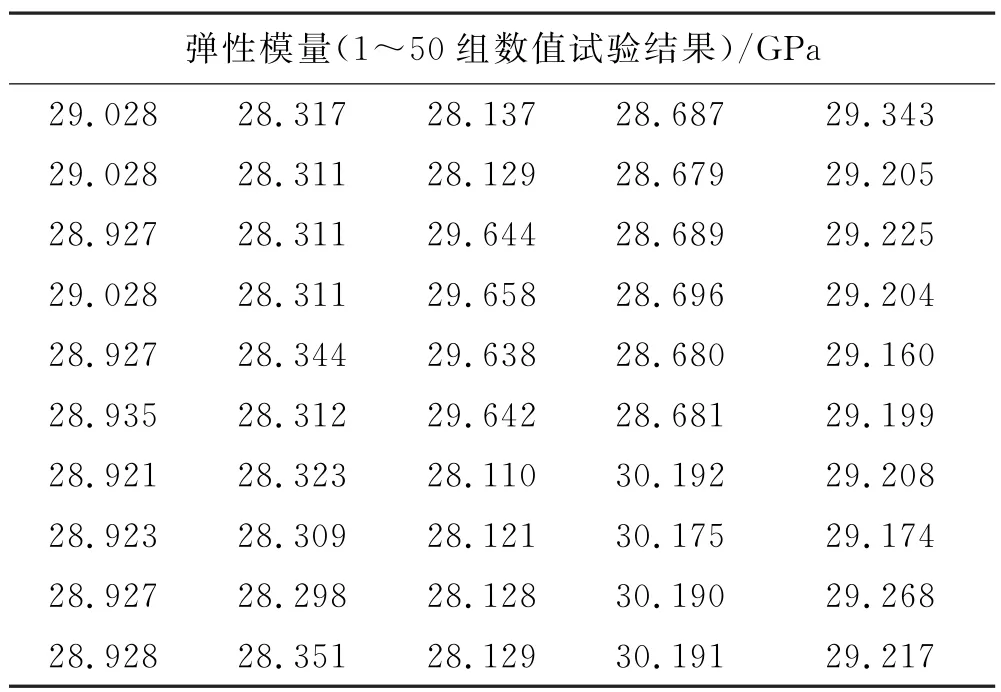
表4 骨料、砂浆及界面的随机性对混凝土弹性模量的影响

表5 骨料、砂浆及界面的随机性对混凝土峰值应变的影响

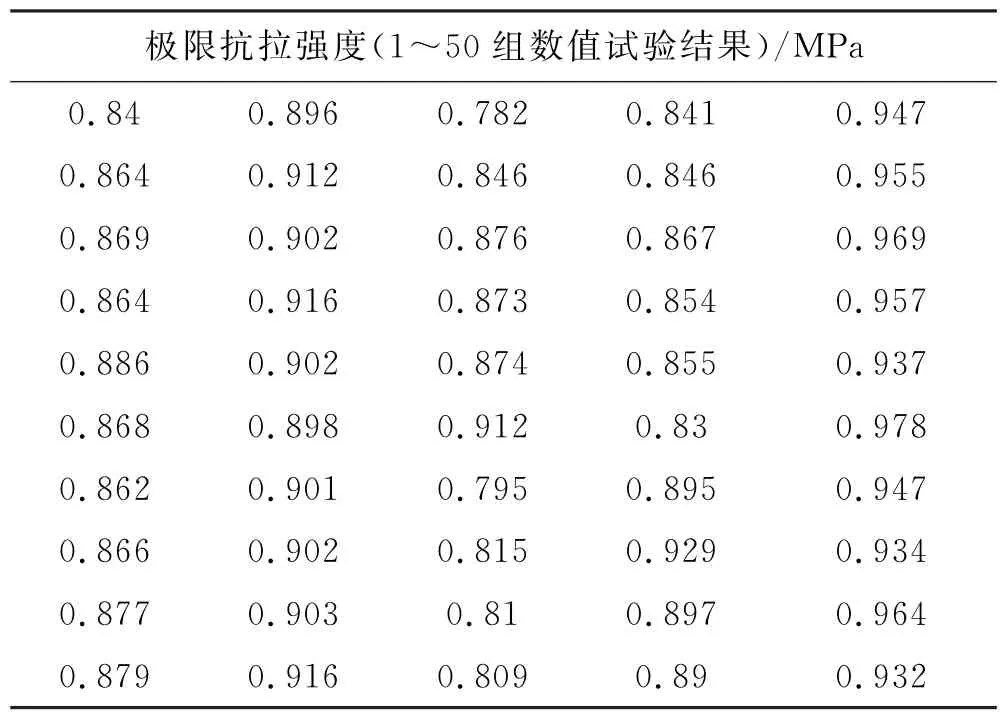
表6 骨料、砂浆及界面的随机性对混凝土极限抗拉强度的影响

由表4～6及式(4)得到,骨料、砂浆和界面的随机性对弹性模量的影响程度为7.2%,对峰值应变的影响程度为17.6%,对极限抗拉强度的影响程度为22.1%,即对极限抗拉强度的影响最大,对峰值应变的影响次之,对弹性模量的影响最小.与表3的结果相比可以发现,骨料的影响大于砂浆和界面的影响,因此以往研究[12-13]中仅考虑骨料的几何随机性,具有一定的事实依据,但是砂浆和界面的力学随机性仍不足以忽视.

2.3 混凝土极限抗拉强度的可靠度分析

基于表6中50组试验的极限抗拉强度,绘制频数分布直方图,如图7所示.

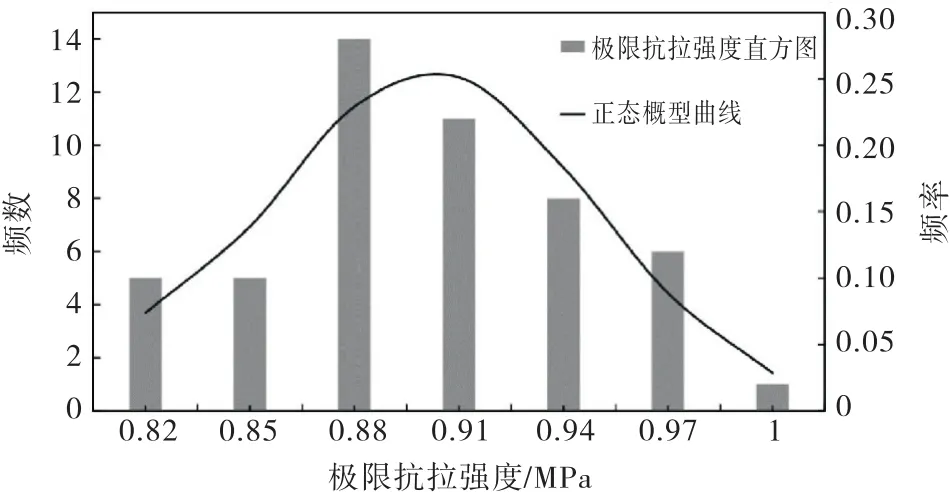
图7 极限抗拉强度直方图与正态概型曲线

假设极限抗拉强度服从正态分布N[0.887,0.0462],利用K-S检验法按显著性水平α=0.05进行非参数检验[24],检验过程如下：记一个正态分布函数F(β),假设随机变量β服从该正态分布函数;S n(β)为样本的经验分布函数.计算F(β)与S n(β),进而得到检验统计量D n.其中S n(β)|.根据显著性水平α及样本容量n,查阅柯尔莫哥洛夫分位数表[25]得到D(n,α).若D(n,α)＞D n,则假设成立,反之假设不成立.具体检验参数见表7.

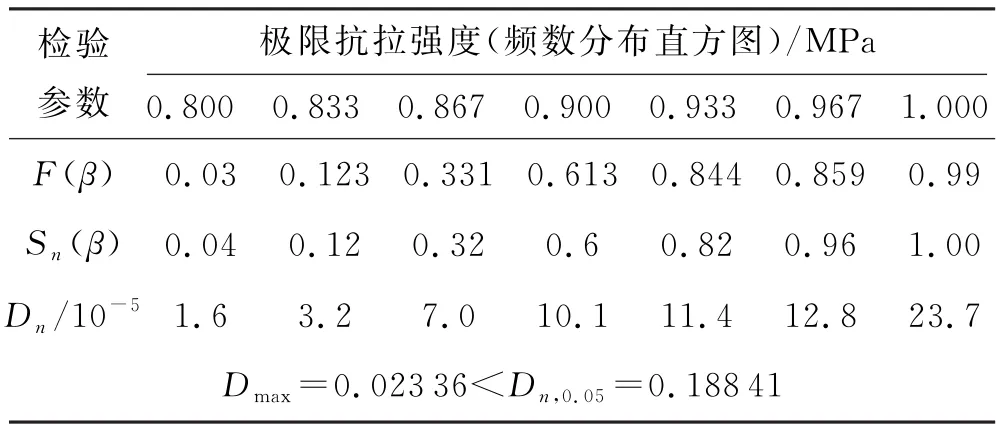
表7 K-S检验结果

检验结果表明在95%保证率下全级配混凝土的极限抗拉强度服从正态分布.

基于正态分布的概率密度函数,计算各级保证率对应的极限抗拉强度,如图8所示.由图可见,随着保证率的提高,极限抗拉强度显著降低,当保证率大于75%时具有加速减小的趋势,说明试验结果的离散性较大,因此砂浆、界面及骨料随机性的影响在研究中不应被忽视.

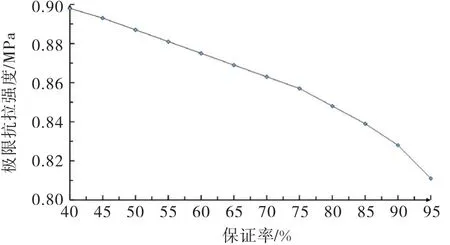
图8 保证率对混凝土极限抗拉强度的影响

3 结 论

本文通过数值试验模拟了全级配混凝土的单轴受拉破坏过程,基于50组试验结果,分析了骨料、砂浆、界面的随机性对全级配混凝土抗拉性能的影响.主要结论如下：

1)骨料、砂浆及界面的随机性对弹性模量的影响较小,对极限抗拉强度和峰值应变的影响较大.其原因可能是：随机性引起的局部弱面容易成为强度"短板",从而显著影响极限抗拉强度和峰值应变,但是局部弱面对试件的整体变形则影响较小,因此随机性对弹性模量的影响较小.上述分析仍需进一步研究.

2)相较骨料的几何随机性,砂浆、界面的力学随机性对混凝土抗拉性能的影响相对较小,但是仍然不应忽略.其原因可能是：混凝土的抗拉性能与试件中裂缝的扩展过程密切相关;由于界面的强度较弱,所以裂缝通常沿界面扩展;骨料的随机分布及随机形状直接影响界面的几何分布,从而显著影响裂缝的路径长短及曲折程度,因此骨料的几何随机性对混凝土抗拉性能的影响较大.上述分析仍需进一步研究.

3)由于骨料的强度远大于砂浆及界面,同时为了简化计算,所以本文假定骨料始终为线弹性(不发生损伤),且具有恒定的弹性模量和泊松比.但是,现实中骨料存在破碎的现象,同时其力学参数也具有随机性,由此产生的影响仍需进一步研究.

4)随机分析虽然会显著增加研究人员的工作量,但是其作用不容忽视.在条件允许的前提下,数值试验中应该采用更多数量的试件.在随机分析中,为了减少研究人员的负担,仍需在建模效率以及计算效率上有所突破.