基于安时-电动势法的锂离子电池组状态估计研究

余 航，张博望麒，易美琪

（1.黑龙江科技大学 电气与控制工程学院，黑龙江 哈尔滨 150022；2.大庆油田有限责任公司 测试技术服务分公司，黑龙江 大庆 163000)

0 引 言

锂离子电池的种种优点吸引着各行各业的研究人员进行开发探索，很多关键性技术得到了突破，实用化阶段的水平越来越高。但是，目前很多方面的研究还不够完善，其中锂电池的荷电状态估计（State of Charge，SOC）研究是比较薄弱的一环，也是当前BMS系统的最大缺陷。锂电池SOC估计的不精确会直接影响电池容量的有效发挥，导致电池缺乏安全可靠性。如果无法确定电池充放电的实时状态，电池均衡系统会失去其应有的作用，影响电池的性能和使用寿命。所以，锂离子电池SOC估计的研究关键在于精确快速地估计SOC值，以及时做出应对和处理措施，更换电池组中达到使用界限的电池，从而确保整个电池组的工作状态。

1 SOC定义

要想准确估计出蓄电池SOC，首先要了解SOC定义[1]。常温下，充电至电池无法再吸收电量时，SOC为100%[2]。同理，放电至电池无法再放出电量时，SOC 为0%[3]。

目前，普遍将SOC定义为电池当前剩余容量与在相同放电条件下充满的电池可放出总容量的比值，即：

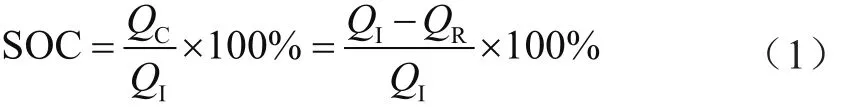
其中QC为电池剩余容量；QI是电池以恒定电流I所能放出的容量；QR为电池已经放出的电量。

2 锂离子电池充放电特性实验

2.1 实验平台

实验选用锂离子电池测试系统、恒温箱和电池数据采集系统。该测试系统可实时检测锂离子电池端电压、电流和工作温度，电压检测误差为2～3 mV，充放电电流检测精度为±0.1%，温度检测精度为±1 ℃，数据采样频率设定为2 Hz，恒温箱可控温度范围-10～100 ℃（±1 ℃）。实验测试装置如图1所示。

2.2 恒流充放电实验

锂离子电池的SOC值与其电动势E之间有稳定的对应关系，即E-SOC曲线。要想实现对SOC的精准估计，前提是提取出稳定精准的锂离子电池E-SOC关系曲线。

图1 实验装置图

锂离子电池的等效电动势等于其内部环境达到平衡时的开路电压。对于锂离子电池而言，当静置时间超过8 h时，可认为电池内部环境已经稳定。为了在保持准确性的前提下，让E-SOC关系曲线提取得更简洁，选用恒流间歇充放电实验。充放电过程中，对锂离子电池进行短时静置，具体的实验流程如图2所示。

提取E-SOC曲线具体步骤：记录锂离子电池充电过程中每个静置时间段内的端电压极小值点，将极小值点进行曲线拟合获得一条曲线，即充电静置曲线；记录锂离子电池放电过程中每个静置时间段内的端电压极大值点，将极大值点进行曲线拟合获得一条曲线，即放电静置曲线；取充电静置曲线与放电静置曲线平均值，该平均值曲线即为锂离子电池的E-SOC曲线[4]，如图3所示。

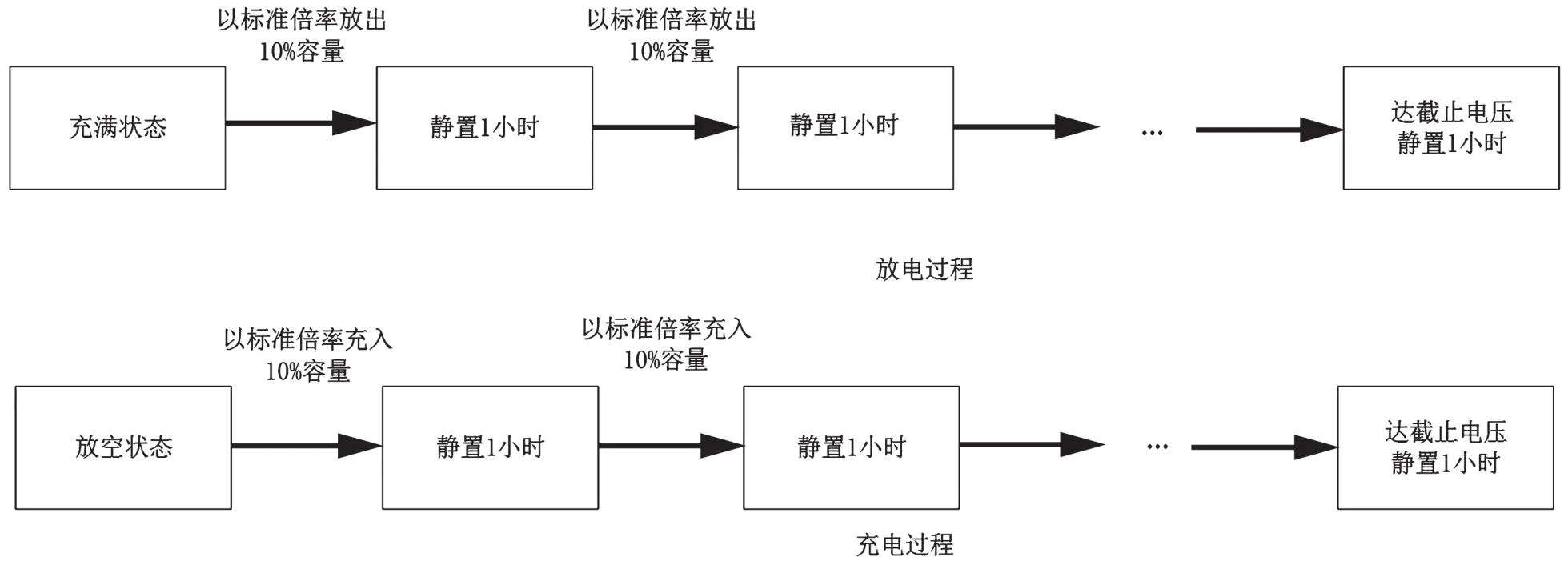
图2 实验流程图

图3 E-SOC曲线

3 基于安时-电动势法的SOC估计

3.1 安时计量法的修正

3.1.1 充放电倍率因素的修正

考虑到充放电倍率会对锂离子电池SOC估计产生影响。因此，估算过程中需要应用Peukert方程进行充放电倍率系数修正。Peukert方程具体表达式如式（2）所示，描述了锂离子电池充放电时的电流与时间的对应关系[5]。

式中，I为充放电电流值，t为电池充、放满电时所需时间，n为电池类型常数，Const是和锂离子电池相关的常数[6]。

代入标准充放电倍率I0和任一充放电倍率Ir，得：

解方程，得：

于是，可得等效充放电倍率系数ki：

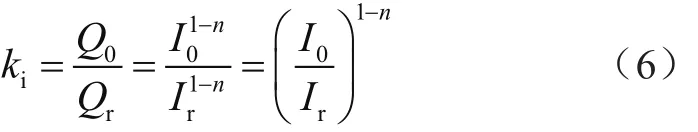
将倍率系数引入标准安时计量法，得：

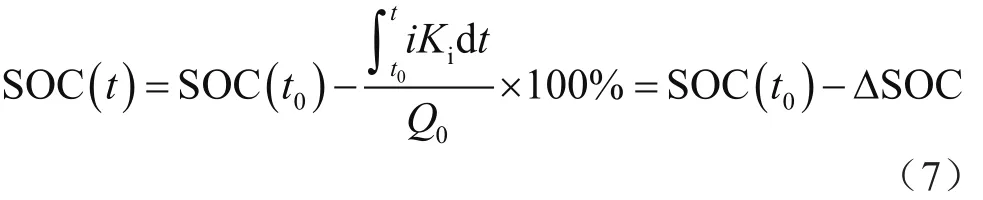
3.1.2 温度系数的修正

温度是影响SOC估计的主要因素[7]，应用经验公式式（8）表达锂离子电池容量与其温度的对应关系[8]。

其中，Q0为锂离子电池在任意温度下时的容量；Q20为锂离子电池在20 ℃时的容量；mT是一个常数温度系数，常规取0.006～0.008。

当KT=[1+mT(T-20)]-1，则QT=Q20/KT。若以 20 ℃作为标准，则Q20就是锂离子电池的额定容量，可将KT作为修正温度系数。修正后的安时计量法为：

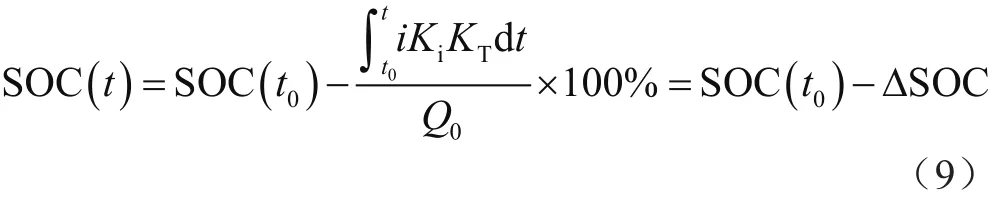
离散化后，即：

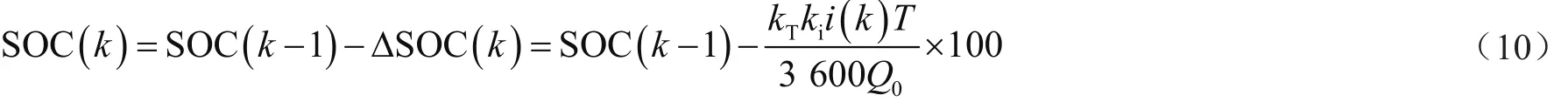
其中，SOC(k)为本拍SOC值；i(k)为本拍电流值；SOC(k-1)为上一拍SOC值；T为安时积分法的计算周期，单位为秒。

然而，估计过程中发现，仅采用安时计量法估计无法确定锂离子电池的初始SOC值，需要结合其他估计方法确定SOC的初值[9]。

3.2 基于等效电动势法的SOC估计

应用等效电动势法的首要任务是建立合适的锂离子电池等效电路模型。等效电路模型很多，如内阻电气模型、Thevenin电气模型、PNGV电气模型以及二阶Randle电气模型等。综合对比几种锂离子等效电气模型，基于以下原因，论文选用了Thevenin模型。

（1）在锂离子电池状态发生变化时，Thevenin模型可以实时反映电池当前的工作状态与工作特性，且误差较小。

（2）在考虑计算精度的情况下，Thevenin等效电气模型结构相对简单，阶数低，在下文电动势计算中，计算过程相对简单。戴维宁电动势模型如图4所示。

图4 戴维宁电动势模型

Thevenin模型等效电路关系为：

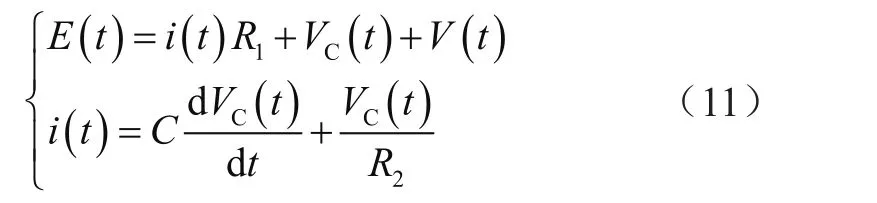
进行拉氏变换，得：

整理后消去VC(s)，可以得到：

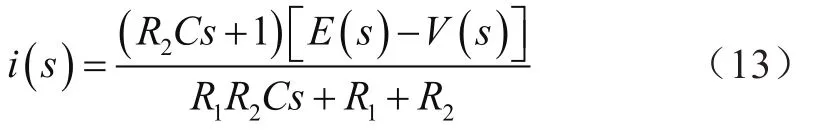
令：

进行Z变换，得：

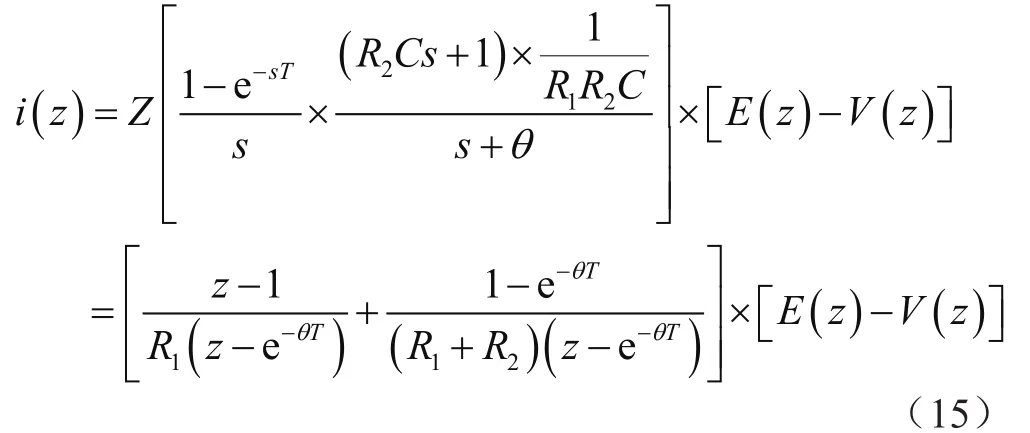
整理后，得：

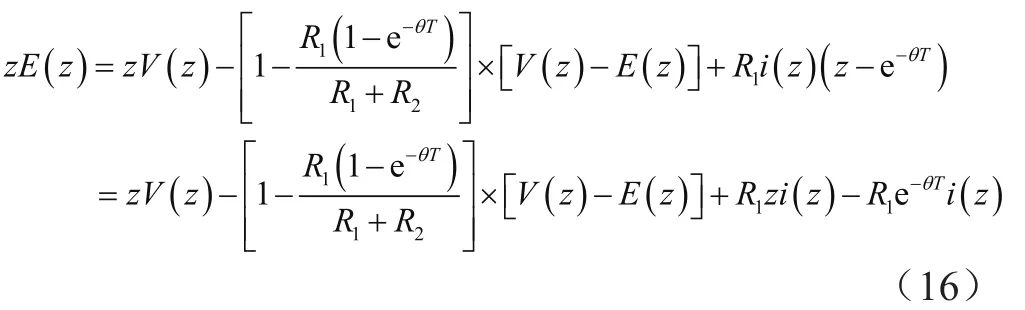
差分方程可写为：

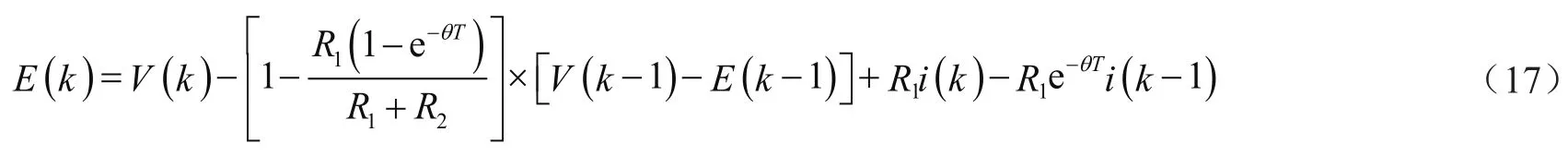
若令：

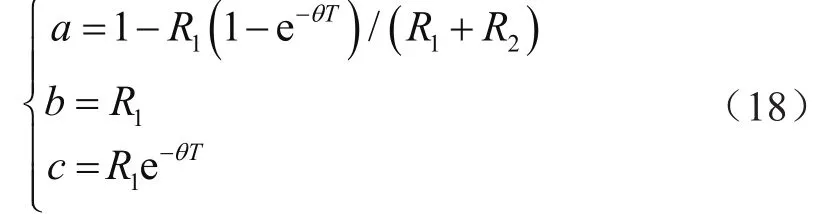
则式（17）可写成：

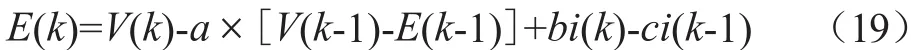
其中，V(k)是本拍的端电压，V(k-1)是上拍端电压，i(k)是本拍电流，i(k-1)是上一拍电流，均为可以从外部直接测量的数值。通过查阅大量文献，得知： 当R1=0.036，R2=0.04，C=3 000时，a=0.967 8，b=0.036，c=0.033 6。将此参数带入递推公式，即可求出电动势E。将求出结果带入E-SOC曲线，即可算出初始SOC值。

3.3 安时法与电动势法的并联加权

将修正后的安时计量法并联加权等效电动势法结合成安时-电动势法。本文选用的安时-电动势法不是两种方法简单的初值加增量加权，如：

其中，SOCA(k)为安时计量法求出的SOC增量，SOCA(k)和SOCE(k)是相对独立的两种计算结果。大部分估计情况下，SOCA(k)和SOCE(k)并不相等。如果简单加权，则计算结果为两个算法的中间值，无法将两种算法的优缺点进行互补。

为了更精准地估计SOC，发挥两种算法的长处，将式（20）中SOCA(k-1)替换为上拍的加权输出SOC(k-1)，形成加权反馈结构，加权反馈具体算法如：

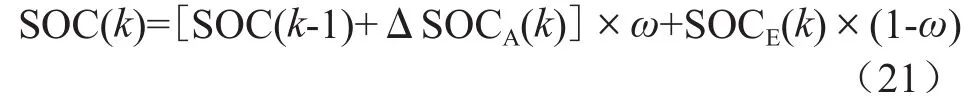
当加权因子ω=0时，SOC(k)=SOCE(k)，即等效电动势法；当ω=1时，即安时计量法；当0＜ω＜1时，即安时计量法与等效电动势法相结合。

算法改进后有以下两方面优势：一方面，当电池工作时即0＜ω＜1时，SOC的估计由等效电动势法计算出的SOC初值与安时计量法计算出的SOC增量并联加权；另一方面，当电池处于静止待工作状态时，此时估计的SOC(k)值收敛于等效电动势法SOCE(k)，即电池的SOC初值。

4 结 论

安时-电动势法是目前较实用的SOC估计方法。将数据带入此方法得到估计曲线如图5所示，绝对百分比误差曲线值如图6所示。通过估计曲线可以发现：在SOC波动范围较小、测试样本较少时，估计效果较好。

图5 估计曲线

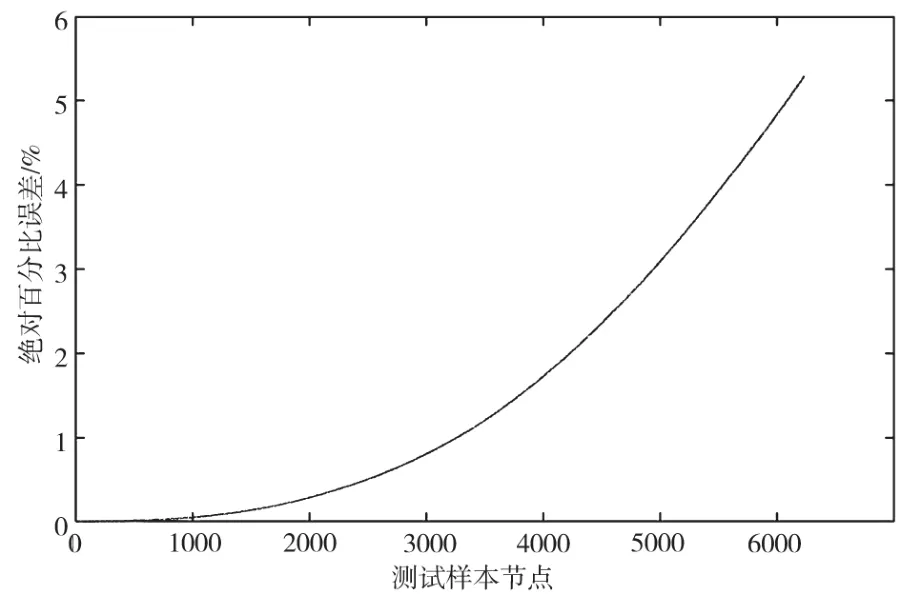
图6 绝对百分比误差