例谈基于辩证思维的高中数学课堂教学提问策略

林庆勇 福建省柘荣县第一中学

引言：辩证思维能力的培养是学生提升数学能力掌握数学思维的核心之一，因此在高中的学习阶段中需要教师给予充分的重视。高中阶段的数学教学具有一定的特殊性，学生不仅需要将分散的知识进行掌握，还需要在知识的学习中逐渐的掌握知识的框架，将知识系统进行提取。这一过程中的进行，就需要学生在学习的过程中具有充分的辩证思维思考能力，这是能力的训练过程，也是能力的展示过程。高中阶段的数学教学内容更加丰富，学生在学习思考的过程中能够发现出更多的可能，因此这正是培养辩证思维能力的重要阶段，提问策略的应用，与培养目标相适应，需要充分应用。

一、在辩证思维培养中提问策略的应用方式

辩证思维的培养需要教师与学生的充分沟通交流，因此学生在课堂中的积极参与是重要的教学引导目标之一。在教学中，教师可以通过应用不同的教学授课方式，使得课程的学习内容与课堂模式之间具有更加紧密的结合，促进师生的交流，进而应用提问策略培养学生的辩证思维能力。

1、应用翻转课堂的模式进行提问教学

在翻转课堂的模式应用中，教师可以将教学的内容以及叫教学的时间进行延展，使得学生在课堂上具有充分的问题思考空间以及问题的探讨空间，积极应用思考方式，提升辩证思维的能力。

例如，在学习高一数学必修五等比数列前n项和公式过程中，教师就需要应用翻转课堂的模式。问题设置，两个人用一分钱与十万元进行交换，连续交换三十天，A在第一天支付给B一分钱，第二天支付两分钱，第三天支付四分钱，以此类推，延续三十天，B能否应用A支付的钱向A支付十万元？

正式的课堂教学开始之前，先将关于这一部分的学习视频以及微课视频资料等提供给学生，使其能够在课下进行自由的观看与学习，对于学习的内容具有较为深入的认识。就普通课堂的问题提问与翻转课堂教学中问题的提出进行对比。在普通教学模式中，教师的问题提出通常应用“对不对？”“是不是？”这样的语句与学生进行沟通，学生在口头上进行积极的反应，但是未能够在脑海中深入的思考问题。在翻转课堂的应用中，教师可以直接对于题目中的关键点进行提问引导，并且从正反两个问题的提出方向进行引导，培养学生的辩证思维能力。

教师可以提问，就以上的问题求解的表达式是什么？

学生将会列出求解表达式求解，S=1+2+22+23+…+230

在这一阶段教师需要向学生进行等比数列基础知识的教授，由表达式是由学生进行列出的，因此学生对于表达式的内容具有较为深刻的认知。在接下来的教学的过程中，教师就等比数列的特性进行提问，以上的表达式具有何种特点？

学生将会回答到，每一项的内容是前一项的二倍。

在这样的提问过程中，学生就能掌握等比数列的基本特性，并且熟悉其应用的方式，通过对于问题正反方向的思考了解到其中的辩证关系【1】。

2、应用小组探讨的模式进行提问的教学

小组探讨的学习模式，可以应用于教学中学生具有较为浓厚趣味的部分进行使用，例如在高中阶段的学习中学生对于立体几何具有较为浓厚的兴趣，教师可以在求解棱锥体积时应用这一教学方式进行教学，培养学生在学习中与其他同学的交流合作能力，从不同的角度思考问题，提升辩证思维能力。

在问题的设置上，教师可以给不同的小组分配不同的探究问题，使得其能够在探究的过程中都发挥出阶段性的作用【2】。

例如：

小组A思考：棱柱的体积公式是什么？并将棱柱的体积公式进行推导。

小组B思考：等高低面积的棱柱体积相等，高相等的两个棱锥体也会呈现出相同的状况吗？

小组C思考：如何求解两个等底面积棱锥的体积？

小组D思考：棱锥的求解公式是什么？

二、基于辩证思维培养的例题分析

辩证思维的培养，教师除了需要重视学生的沟通交流，更为重要的是需要将思维运用在题目的分析与实践中，逐渐的将思维能力的提升与解题能力的提升相结合，提升对于数学问题中矛盾的认知程度，从而将辩证思维能力进行提高。

例题的在应用的过程中需要对于两个方面进行重视，其一是教师在进行例题的讲解以及引导之前，需要保证学生已经使用该例题进行过练习；其二是教师在例题的引导求解中，需要用两种以上的思维方式进行答案的求解，促使学生能够从不同的方面思考数学的问题【3】。

1、利用辩证思维法分析题目

例如，甲、乙两人约定晚上 6 时到 7 时之间在城市中某一咖啡店会面，由于二者在路程上不同，因此到达的时间并不一致，其后有其他的任务要进行，于是甲、乙约定先到者应等候另一人半小时，过时即可离去，根据上述的条件，求两人能会面的概率。

分析：这是较为典型的概率问题，由于其中的数据不明确，在解题时需要应用设未知数的方式。可以结合作图进行分析，其中最为关键的部分，在于图画中能够重合的部分，即表示二人能够会面的几率。在解题的引导中，教师除了需要引导学生就具体的问题进行解决之外，还需要对于数形结合的方法进行强调，这种方式的应用就是基于辩证思维，能够应用几何内容与代数内容进行结合，对于题目条件中不充分的内容进行补充。

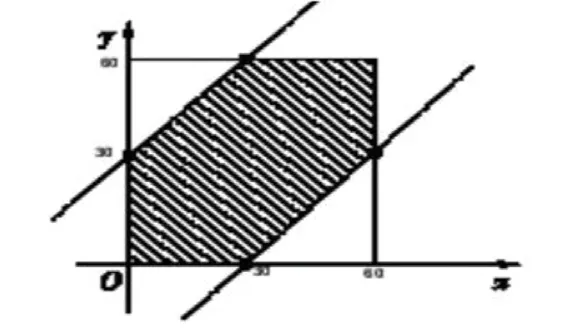
图一

如图一所示，以轴和轴分别表示甲、乙两人在晚上 6 时到 7 时之间到达约定地点的时间，则两个人能够见面当且仅当 x- y ≤30，在平面直角坐标系xoy 下， （x,y） 所有可能结果是边长为 60 的正方形，而事件 A“两人能够会面”的可能结果由图中的阴影部分表示，最后由几何概率公式可求。这是概率统计中，相当不错的数形结合范例之一，教师需要应用这种典型的范例，引导学生树立正确的解题意识，应用辩证思维的方式，寻找其中的突破口，进而对于题目进行解答，并且对于这一类型的题目有所了解认知【4】。

2、利用辩证思维法寻找题目的关键点

高中阶段的数学学习以及考察的方式都呈现出具有较强综合性的特点，因此，在教学的过程中，教师需要引导学生对于题目中复杂的信息进行分析，将其中的有效信息筛选出来，并且根据将信息与题目提问进行结合，分析题目的题眼所在之处，即是解题的关键点。

例：已知函数y=f(x)(x∈R)的导函数为f'(x)。若f(x)－f(－x)=2x3，且当x≥0时，f'(x)＞3x2，则不等式f(x)－f(x －1)＞3x2－3x+1的解集是。

从所求问题“不等式 f(x)－f(x－1)＞3x2－3x+1的解集”，这个粗略方向思考，可判定为抽象函数与不等式结合，应利用抽象函数的单调性，故联系导函数的不等式，构造新函数F(x)=f(x)－x3，即F'(x)=f'(x)－3x2＞0可以确定函数的单调性，然后再思考给定条件f(x)－f(－x)=2x3的应用，可变为f(x)－x3=f(－x)－(－x)3，则F(x)是奇函数，于是问题可化F(x)＞F(x－1)，从而解题水到渠成【5】。

结束语：

高中数学学习的过程，是学生实现数学能力提升以及飞跃的重要阶段，因此，在教师的教学时，不能够仅仅对于学生具体的知识掌握进行重视，也需要逐渐的关注学生学习的其他方面，促进学生构建学科的知识框架、掌握学科的思维，并且将思维的能力运用在题目的求解过程中。通过题目的练习以及教师的引导，学生将会逐渐的发现自己的思维能力得到提升，能够运用辩证思维的方式，一分为二的看待数学问题，并且逐渐将这种思维方式应用于生活中，提升个人的综合素质。辩证法是马克思主义哲学的精华部分，在学生今后的学习与成长中，必将产生深刻的影响，需要教师在学科教学中进行具体的引导，提升学生能力。